Wielościany Catalana (bryły Catalana) – wielościany dualne do wielościanów archimedesowych^[1]. Wielościan dualny powstaje przez zastąpienie każdej ściany wierzchołkiem, a każdego wierzchołka ścianą.

Wszystkie wielościany są wypukłe. Ich grupy symetrii są przechodnie ze względu na ściany, ale nieprzechodnie ze względu na wierzchołki. Jest tak, ponieważ dualne do nich wielościany archimedesowe mają grupy symetrii przechodnie ze względu na wierzchołki i nieprzechodnie ze względu na ściany. W przeciwieństwie do brył platońskich i brył archimedesowych, ściany brył Catalana nie są wielokątami foremnymi. Ponadto dwie z brył Catalana mają grupy symetrii przechodnie ze względu na krawędzie: dwunastościan rombowy i trzydziestościan rombowy.

Dwa z wielościanów Catalana są chiralne: dwudziestoczterościan pięciokątny i sześćdziesięciościan pięciokątny, dualne do chiralnych brył Archimedesa: sześcio-ośmiościanu przyciętego i dwudziesto-dwunastościanu przyciętego.

Nazwa pochodzi od nazwiska belgijskiego matematyka Eugèna Charlesa Catalana.

Nazwa(s)	Rysunek obrotowy bryły	Siatka	Wielościan dualny (bryła Archimedesa)	Ściany	Krawędzie	Wierzchołki	Konfiguracja ścian	Symetria
czworościan potrójny		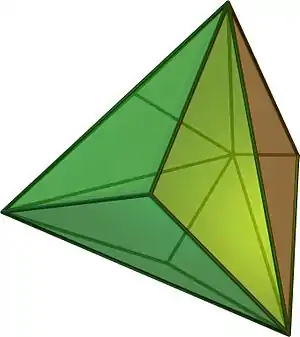	czworościan ścięty	12	18	8	trójkąt równoramienny V3.6.6	${\displaystyle T_{d}}$
dwunastościan rombowy		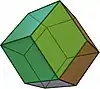	sześcio-ośmiościan	12	24	14	Romb V3.4.3.4	${\displaystyle O_{h}}$
ośmiościan potrójny		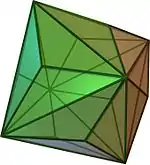	sześcian ścięty	24	36	14	trójkąt równoramienny V3.8.8	${\displaystyle O_{h}}$
sześcian poczwórny		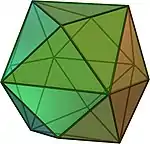	ośmiościan ścięty	24	36	14	trójkąt równoramienny V4.6.6	${\displaystyle O_{h}}$
dwudziestoczterościan deltoidowy		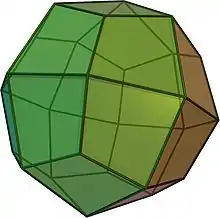	sześcio-ośmiościan rombowy mały	24	48	26	Deltoid V3.4.4.4	${\displaystyle O_{h}}$
ośmiościan szóstkowy		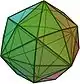	sześcio-ośmiościan ścięty	48	72	26	trójkąt różnoboczny V4.6.8	${\displaystyle O_{h}}$
dwudziestoczterościan pięciokątny			sześcio-ośmiościan przycięty	24	60	38	pięciokąt nieforemny V3.3.3.3.4	${\displaystyle O}$
trzydziestościan rombowy		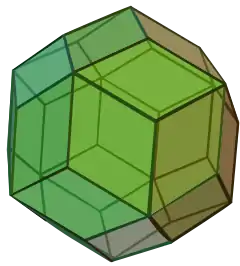	dwudziesto-dwunastościan	30	60	32	Romb V3.5.3.5	${\displaystyle I_{h}}$
dwudziestościan potrójny		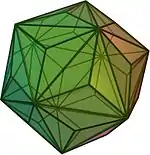	dwunastościan ścięty	60	90	32	trójkąt równoramienny V3.10.10	${\displaystyle I_{h}}$
dwunastościan piątkowy		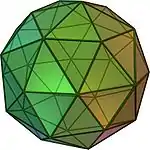	dwudziestościan ścięty	60	90	32	trójkąt równoramienny V5.6.6	${\displaystyle I_{h}}$
sześćdziesięciościan deltoidalny			dwudziesto-dwunastościan rombowy mały	60	120	62	deltoid V3.4.5.4	${\displaystyle I_{h}}$
dwudziestościan szóstkowy			dwudziesto-dwunastościan ścięty	120	180	62	trójkąt różnoboczny V4.6.10	${\displaystyle I_{h}}$
sześćdziesięciościan pięciokątny			dwudziesto-dwunastościan przycięty	60	150	92	pięciokąt nieforemny V3.3.3.3.5	${\displaystyle I}$

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Catalan Solid, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-18].