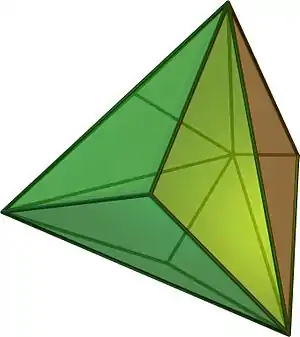
Czworościan potrójny

Czworościan potrójny – wielościan będący dualnym do wielościanu Archimedesa lub, inaczej mówiąc, wielościanem Catalana. Dualny do niego jest czworościan ścięty.

Można go sobie wyobrażać jako czworościan z doklejonymi do każdej ściany ostrosłupami trójkątnymi; jest to więc wielościan gwiaździsty zbudowany na czworościanie. Interpretacja ta wyjaśnia nazwę.

Jeżeli krótsze krawędzie czworościanu potrójnego mają długość 1, to pole jego powierzchni jest równe ${\displaystyle {\frac {5}{3}}{\sqrt {11}},}$ a objętość ${\displaystyle {\frac {25}{36}}{\sqrt {2}}.}$

Związek z geometrią czterowymiarową

Czworościan potrójny, którego ściany są trójkątami równobocznymi jest siatką czterowymiarowego wielościanu foremnego nazywanego 5-komórką (czterowymiarowy odpowiednik czworościanu).

Stellacje

Stellacja czworościanu potrójnego

Ta figura chiralna jest jedną z trzynastu stellacji wynikających z reguł Millera.

Zobacz też

• ścięty czworościan potrójny

Bibliografia

• Section 3-9. W: The Geometrical Foundation of Natural Structure.brak strony w książce
• The thirteen semiregular convex polyhedra and their duals. W: Magnus Wenninger: Dual Models. Cambridge University Press, 1983, s. 14. MR730208. ISBN 978-0-521-54325-5.
• Chapter 21. Naming the Archimedean and Catalan polyhedra and tilings. W: John H. Conway, Heidi Burgiel, Chaim Goodman-Strass: The Symmetries of Things. 2008, s. 284. ISBN 978-1-56881-220-5.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Triakis Tetrahedron, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).