Funkcja rzeczywista zmiennej rzeczywistej mająca trzy punkty stałe

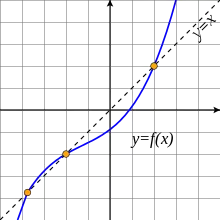
Punkt stały odwzorowania pewnego zbioru w siebie – argument funkcji, dla którego jej wartość jest mu równa. Formalnie: jeśli ${\displaystyle X}$ jest zbiorem, a ${\displaystyle f\colon X\to X}$ funkcją na nim, to jej punktem stałym jest każdy element ${\displaystyle x\in X}$ spełniający równanie^[1]:

${\displaystyle f(x)=x.}$

Nie musi to być punkt w sensie geometrycznym; punktem stałym może być liczba, wektor, ciąg, macierz, inna funkcja, figura lub inny zbiór. Ogół wszystkich punktów stałych danej funkcji oznacza się:

${\displaystyle \operatorname {Fix} (f):=\{x\in X\colon \;f(x)=x\}.}$

W różnych dziedzinach matematyki jak algebra, analiza czy topologia udowodniono twierdzenia o punkcie stałym gwarantujące istnienie takich argumentów dla pewnych typów funkcji. Tak powstała cała dyscyplina poświęcona tego typu zagadnieniom: teoria punktu stałego.

Istnieją uogólnienia tego pojęcia jak:

• punkt okresowy definiowany dla dowolnej funkcji wewnątrz zbioru;
• wektor własny określony dla endomorfizmów liniowych i macierzy kwadratowych.

Zastosowania

Część zagadnień matematycznych można sprowadzić do poszukiwania punktów stałych. Przykłady to:

• szukanie optymalnych rozwiązań w teorii gier (zastosowania w ekonomii),
• istnienie rozwiązań pewnych równań różniczkowych,
• szukanie punktów stałych odwzorowań zbiorów częściowo uporządkowanych (zastosowania w informatyce)
• pewne zagadnienia teorii układów dynamicznych i teorii chaosu.

Także rozwiązywanie układu równań, np. liczbowych, sprowadza się do szukania punktu stałego pewnej funkcji. Dokładniej, niech ${\displaystyle X}$ będzie przestrzenią liniową (np. ${\displaystyle \mathbb {R} ^{n}}$ lub ${\displaystyle \mathbb {C} ^{n}}$) oraz ${\displaystyle F\colon X\to X.}$ Punkt ${\displaystyle x\in X}$ jest rozwiązaniem równania ${\displaystyle F(x)=0}$ wtedy i tylko wtedy, gdy jest punktem stałym odwzorowania ${\displaystyle f={\mbox{id}}-F.}$

Zobacz też

• nieporządek
• palindromy – punkty stałe odwrócenia (inwersji) ciągu
• własność punktu stałego

Przypisy

Bibliografia

• Jerzy Jezierski, Wacław Marzantowicz: Homotopy Methods in Topological Fixed and Periodic Points Theory. Dordrecht: Springer, 2006.brak strony w książce

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Fixed Point, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-10-10].
• Fixed point (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-10-10].
• Michael Stevens, Fixed Points, kanał Vsauce na YouTube, 28 września 2016 [dostęp 2021-03-15].