
Teoria liczb – dziedzina matematyki badająca własności niektórych typów liczb[uwaga 1]. Początkowo analizowała tylko liczby naturalne i wymierne, później rozszerzając zakres o inne liczby rzeczywiste, zwłaszcza algebraiczne[1]. Przynajmniej częściowo jest zaliczana do matematyki dyskretnej[2].
Jest to jedna z najstarszych dziedzin matematyki obok geometrii; obie dyscypliny od starożytności nie przestają na siebie oddziaływać. Rozwój teorii liczb miał też wpływ na inne gałęzie matematyki jak algebra[1] – w tym ogólna algebra przemienna – oraz geometria algebraiczna, analiza zespolona i probabilistyka[3]. Kierunek zastosowań jest też odwrotny: teoria liczb sama skorzystała z osiągnięć algebry, geometrii algebraicznej i probabilistyki[1]. Niektóre z wykorzystywanych metod są zaawansowane jak np. algebra homologiczna[1] i abstrakcyjna analiza harmoniczna[3]. Teoria liczb obfituje w problemy otwarte postawione elementarnie – tj. zrozumiałe dla laików, nawet dla dzieci – ale czekające na rozwiązanie wyjątkowo długo, czasem stulecia. Niektóre z pytań zadanych w XVIII wieku – jak hipoteza Goldbacha i hipoteza prostopadłościanu idealnego – do dzisiaj pozostają bez odpowiedzi. Teorią liczb zajmowali się matematycy zaliczani do najwybitniejszych w historii jak Leonhard Euler, Carl Friedrich Gauss i Bernhard Riemann; wkład w tę dziedzinę nagradzano też najwyższymi zaszczytami w matematyce jak Medal Fieldsa, Nagroda Abela czy Medal Copleya przyznawany także innym naukowcom. Istnieją również nagrody poświęcone tej konkretnej dziedzinie – odpowiednie kategorie Nagrody Cole’a i Nagrody Fermata. Teorię liczb nazywano „królową matematyki”[3][4].
W II połowie XX wieku znaleziono zastosowania tej dyscypliny w kryptologii i fizyce matematycznej, zwłaszcza kwantowej teorii pola, teorii strun oraz teorii kwantowego chaosu[5]. Powstało całe czasopismo naukowe poświęcone związkom teorii liczb z fizyką[6]. Ta dziedzina matematyki wywarła też pewien wpływ na popkulturę; amatorskie badania wielkiego twierdzenia Fermata są motywem powieści młodzieżowej Szatan z siódmej klasy Kornela Makuszyńskiego (1937).
Podział teorii liczb
Główne działy teorii liczb to[7]:
- elementarna teoria liczb,
- algebraiczna teoria liczb,
- analityczna teoria liczb,
- geometryczna teoria liczb,
- probabilistyczna teoria liczb,
- kombinatoryczna teoria liczb[10],
- teoria sit.
Elementarna teoria liczb jest jej najstarszym działem; nie stosuje się w niej metod teorii funkcji analitycznych[11], jednakże w analitycznej teorii liczb stosuje się czasem metody elementarne[11][12]. Do najważniejszych osiągnięć metod elementarnych teorii liczb należą dowody Erdősa i Selberga twierdzenia o dystrybucji liczb pierwszych (ich dowody były niezależne, ale oba oparte na lemacie Selberga)[12]. Teoria liczb zajmuje się również rozwiązywaniem równań w dziedzinie liczb naturalnych, całkowitych, wymiernych, algebraicznych (całkowitych i wymiernych) oraz (od niedawna) liczb p-adycznych[13].
Według Iwańca i Kowalskiego, jako kryterium stosowane do tego, aby dane zagadnienie z teorii liczb można było zakwalifikować do analitycznej teorii liczb jest to, czy wykorzystuje się w nim analizę zespoloną. Zamienne, jako kryterium można również uznać występowanie analizy harmonicznej. Przez długi czas prace z analitycznej teorii liczb wykorzystywały jedynie abelową analizę harmoniczną (dot. grup przemiennych). Współcześnie częściej wykorzystuje się również funkcje automorficzne. Nowe metody wywodzą się m.in. z analizy spektralnej i wyników Maassa czy Selberga[11].
Geometryczna teoria liczb korzysta z geometrii do badania liczb algebraicznych. Pierścień algebraicznych liczb całkowitych utożsamia się ze zbiorem punktów kratowych w [14]. Pierwsze prace z tej dziedziny zostały napisane przez Hermanna Minkowskiego[15].
Probabilistyczna teoria liczb korzysta z metod probabilistycznych do analizy zagadnień teorii liczb[16]. W szczególności, jest to np. centralne twierdzenie graniczne[17]. Przykładowo, Soundararajan i Radziwiłł korzystają z niego dla badania wartości logarytmu zespolonego funkcji zeta na linii krytycznej [18].
Kombinatoryczna teoria liczb korzysta w swoich badaniach z wyników teorii liczb, kombinatoryki, analizy harmonicznej i teorii ergodycznej. Przykładowo, twierdzenie Greena-Tao wykorzystuje twierdzenie Szemerédiego zmodyfikowane dla liczb pierwszych[19][20].
Niektórych gałęzi teorii liczb nie można jednoznacznie zaklasyfikować do danego działu, metody mogą się między nimi przeplatać. Przykładem może być teoria sit, która korzysta przede wszystkim z twierdzeń elementarnych, ale bywa nazywana poddziedziną analitycznej teorii liczb, ponieważ korzysta z części jej wyników. Dodatkowo, w ostatnich pracach naukowych metody sit bywają często przeplatane z metodami analitycznej teorii liczb lub innych dziedzin[21].
Historia
Starożytność i średniowiecze

Początki teorii liczb sięgają starożytności; przykładowo starożytni mieszkańcy Mezopotamii oraz Egiptu mogli rozważać problem trójek pitagorejskich. Największe postępy w tej dziedzinie zrobiła jednak kultura starogrecka. Odnotowano serię postępów na przestrzeni niecałego tysiąclecia, od okresu klasycznego do czasów cesarskiego panowania rzymskiego:
- Pitagorejczycy opisali:
- liczby niewymierne na przykładzie pierwiastka kwadratowego z dwójki;
- liczby zaprzyjaźnione;
- o niewymierności pierwiastków z liczb naturalnych pisał też potem Teodor z Cyreny;
- Euklides z Aleksandrii w dziele Elementy wyłożył:
- algorytm Euklidesa znajdowania największego wspólnego dzielnika,
- dowód, że istnieje nieskończenie wiele liczb pierwszych[1];
- zasadnicze twierdzenie arytmetyki oparte o lemat Euklidesa;
- sposób znajdowania niektórych liczb doskonałych;
- Eratostenesowi przypisuje się metodę znajdowania liczb pierwszych: sito Eratostenesa;
- Diofantos został upamiętniony nazwą równań diofantycznych[1].
Teorią liczb mógł się zajmować także Archimedes, ale raczej marginesowo; nowe odkrycia historyczne mogą ten pogląd zmienić.
Równolegle rozwijano matematykę w Indiach, w sposób komplementarny do tego greckiego i znaczący dla teorii liczb. Systemy pozycyjne uprościły wiele obliczeń i pozwoliły na sformułowanie cech podzielności liczb całkowitych. Matematycy chińscy rozważali za to układy kongruencji, na temat których udowodnili chińskie twierdzenie o resztach. Uczeni arabscy mieli w tę dziedzinę ograniczony wkład – w matematyce skupili się na trygonometrii i algebrze[22], choć ta druga dziedzina później wpłynęła na rozwój teorii liczb.
W XIII-wiecznych Włoszech kupiec Leonardo Fibonacci podał jedną z metod generowania trójek pitagorejskich, a oprócz tego opisał ciąg Fibonacciego, również istotny z punktu widzenia teorii liczb. Problem nieskończoności liczb pierwszych w tym ciągu w lutym 2022 pozostaje otwarty.
XVII wiek

XVII wiek to umowny początek nowożytnej teorii liczb i jej statusu samodzielnej nauki[22]. Rozwijał ją wtedy Pierre de Fermat i miał w tej dziedzinie co najmniej pięć znaczących osiągnięć:
- małe twierdzenie Fermata[1], na którym opiera się m.in. test pierwszości Fermata;
- hipoteza zwana Wielkim Twierdzeniem Fermata, udowodniona potem w XX wieku[1];
- badania liczb Fermata; wysunął hipotezę, że wszystkie z nich są liczbami pierwszymi. Leonhard Euler obalił ją kontrprzykładem, a do tej pory (luty 2022) nie znaleziono żadnego dalszego przykładu liczby pierwszej Fermata. Jest to sugestia, że prawdziwe może być twierdzenie przeciwne – brak liczb pierwszych Fermata dalszych niż te, które sam znalazł;
- twierdzenie Fermata o sumie dwóch kwadratów;
- algorytm Fermata faktoryzacji liczb całkowitych.
W tym samym stuleciu:
- Marin Mersenne badał pewien ciąg liczbowy, nazwany potem liczbami Mersenne’a. Znalazł w nim nowe liczby pierwsze; w dalszych stuleciach znajdowano w nim jeszcze więcej takich liczb, co prowadzi do pytania, czy jest ich nieskończenie wiele. Znaleziono też związek liczb pierwszych Mersenne’a z rozważanymi od starożytności liczbami doskonałymi[23];
- John Pell rozważał także pewne kwadratowe równanie diofantyczne nazwane potem od jego nazwiska (równanie Pella). Zrobił to jako pierwszy w Europie, choć już tysiąclecie wcześniej badali je matematycy indyjscy.
XVII wiek to także narodziny nowych dziedzin matematyki, które okazały się istotne dla teorii liczb:
- geometria analityczna dała nową, graficzną perspektywę na pewne fakty i problemy. Przykładowo rozwiązania równań diofantycznych to punkty kratowe odpowiednich krzywych itp. figur w kartezjańskim układzie współrzędnych; trójki pitagorejskie odpowiadają punktom kratowym okręgów o całkowitym promieniu. Geometria analityczna jest też korzeniem geometrii algebraicznej, blisko związanej z teorią liczb;
- analiza poszerzyła zakres badań arytmetyki i jej metody. Wprowadzona tam podstawa logarytmu naturalnego (e) stała się przedmiotem dociekań, a nowe tożsamości związane z liczbą pi (π) pozwoliły potem udowodnić jej niewymierność. Związki teorii liczb z analizą zacieśniły się później w XIX wieku;
- probabilistyka dostarczyła teorii liczb nowych metod[1], m.in. algorytmów.
XVIII wiek

W XVIII wieku Leonhard Euler – jak wspomniano wyżej – obalił hipotezę Fermata o liczbach nazwanych jego nazwiskiem[23]. Oprócz tego Euler:
- uogólnił małe twierdzenie Fermata na inne dzielniki (moduły), niekoniecznie pierwsze;
- podał rekordowo dużą liczbę pierwszą;
- w 1744 udowodnił, że suma odwrotności liczb pierwszych jest nieskończona (jest to szereg rozbieżny)[24]; rozszerzył tym znany wcześniej fakt o nieskończoności liczb pierwszych;
- wykazał, że każda parzysta liczba doskonała ma związek z liczbami pierwszymi Mersenne’a[23];
- udowodnił, że podstawa logarytmu naturalnego (e) jest niewymierna. Był to pierwszy dowód niewymierności od czasów starożytnych;
- wprowadził stałą nazywaną od jego nazwiska, co zrobił potem niezależnie Lorenzo Mascheroni. Wymierność stałej γ była potem długo badana przez matematyków, a w lutym 2022 roku pozostaje to problem otwarty;
- wysunął pewną hipotezę o sumach potęg, jednak obalono ją w XX wieku metodami komputerowymi.
Postępy poczynili też inni matematycy:
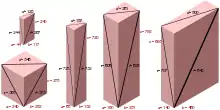
- W 1719 roku Paul Halcke podał pierwszy przykład cegiełki Eulera, tj. prostopadłościanu o całkowitych krawędziach i przekątnych ścian. Jego rozwiązanie odpowiedniego układu równań diofantycznych to (44,117,240). Doprowadziło to do pytania o prostopadłościan idealny, mający dodatkowo całkowitą przekątną (główną); w lutym 2022 problem pozostaje otwarty.
- Johann Heinrich Lambert udowodnił niewymierność liczby pi (π).
- Christian Goldbach wysunął pewną hipotezę o liczbach pierwszych, nazwaną potem hipotezą Goldbacha. W XXI wieku ogłoszono dowód jej słabszej wersji, w lutym 2022 czekający na pełną weryfikację.
- Joseph Louis Lagrange udowodnił twierdzenie nazwane jego nazwiskiem. Mówi ono, że każda liczba naturalna jest sumą czterech kwadratów naturalnych;
- Edward Waring rozwinął też badania problemu Waringa. Jego uczeń wysunął hipotezę nazywaną twierdzeniem Wilsona; zostało udowodnione jeszcze w tamtym stuleciu przez Lagrange’a i jest warunkiem równoważnym pierwszości liczby naturalnej.
XIX wiek

XIX wiek to narodziny nowych gałęzi w teorii liczb:
- Carl Friedrich Gauss otworzył algebraiczną teorię liczb, wprowadzając kongruencje, dowodząc lematu Gaussa i prawa wzajemności reszt kwadratowych[1];
- Bernhard Riemann i August Ferdinand Möbius to pionierzy analitycznej teorii liczb, w której wysunięto m.in. hipotezę Riemanna;
- Joseph Liouville udowodnił istnienie liczb przestępnych. Charles Hermite udowodnił, że należy do nich e (stała Eulera), a Ferdinand Lindemann wykazał przestępność pi (π). Pokrewnym tematem jest aproksymacja diofantyczna liczb niewymiernych, o której Peter Gustav Lejeune Dirichlet udowodnił znaczące twierdzenie;
- Hermann Minkowski zapoczątkował geometrię arytmetyczną[1].
Rozwinięto też „klasyczne” badania liczb naturalnych:
- w 1850 Pafnutij Czebyszow udowodnił postulat Bertranda o rozmieszczeniu liczb pierwszych[25], przez co wynik ten nazwano również twierdzeniem Czebyszowa.
- Eugène Charles Catalan wysunął też hipotezę o nierozwiązywalności pewnego równana diofantycznego. Na rozstrzygnięcie czekała do XXI wieku.
- Twierdzenie Gaussa-Wantzela pokazało związek teorii liczb z geometrią płaską (planimetrią), a konkretniej teorią konstrukcji klasycznych. Problem liczb pierwszych Fermata okazał się istotny dla konstruowalności wielokątów foremnych.
Ogłoszone na koniec stulecia 23 problemy Hilberta zawierały kilka pytań z teorii liczb jak hipotezy Riemanna i Golbacha.
XX wiek

Postęp w teorii liczb naturalnych był wieloraki – rozwiązano niektóre stare problemy oraz postawiono nowe:
- Najpóźniej wtedy sformułowano hipotezę o nieskończoności bliźniaczych liczb pierwszych. Viggo Brun zredukował ten problem do badania wymierności stałej nazwanej od jego nazwiska (B2).
- Pojawił się też problem Collatza o zachowaniu pewnej funkcji lub równoważnie – rodziny ciągów liczb naturalnych.
- Srinivasa Ramanujan zainspirował badania liczb taksówkowych – pewnego rodzaju sum dwóch sześcianów naturalnych;
- Hillel Furstenberg zastosował w teorii liczb topologię, podając nowy dowód twierdzenia Euklidesa o nieskończoności liczb pierwszych.
- Znaczące osiągnięcia przyniosły też obliczenia komputerowe – m.in.:
- obaliły hipotezę Pólyi o własnościach czynników pierwszych (1958);
- obaliły hipotezę Eulera uogólniającą wielkie twierdzenie Fermata (1966);
- rozwiązały jedno z sześciennych równań diofantycznych: x3+y3+z3 = 30 (1999)[26].
- W latach 90. Andrew Wiles udowodnił wielkie twierdzenie Fermata po przeszło 300 latach zmagań matematyków z tym problemem.
- Również w tamtej dekadzie Peter Shor opublikował nowy algorytm faktoryzacji, aktywnie badany przez informatykę kwantową.
- W XX wieku rozwinięto też sprawdzanie pierwszości, opracowując algorytmy o coraz lepszej złożoności obliczeniowej.
Naświetlono również same fundamenty arytmetyki liczb naturalnych. Kurt Gödel w swoim pierwszym twierdzeniu o niezupełności wykazał, że nie może ona być jednocześnie zupełna i niesprzeczna. Wśród nowo poznanych liczb pierwszych znalazły się osobliwości jak liczba Belfegora. Nie dość, że w zapisie dziesiętnym jest palindromem, to jeszcze zawiera w nim liczbę bestii (666), a liczba zer po obu stronach tego symbolu wynosi 13 – także oznakę nieszczęść.
Posunięto też badania nad niewymiernością i przestępnością:
- w 1934 udowodniono twierdzenie Gelfonda-Schneidera, rozwiązujące jeden z problemów Hilberta[27];
- w latach 70. Mitchell Jay Feigenbaum w swoich pracach nad teorią chaosu wprowadził dwie nowe stałe liczbowe, nazwane jego nazwiskiem (α i δ). Ich wymierność stała się przedmiotem analiz;
- w 1979 roku Roger Apéry udowodnił, że suma ζ(3), nazwana potem stałą Apéry’ego, jest niewymierna.
Wiek XX przyniósł też zastosowania dla teorii liczb – w latach 70. rozbudowano kryptografię klucza publicznego, w tym szyfr RSA; opisano także pierwsze związki teorii liczb z fizyką.
Stulecie zwieńczono ogłoszeniem listy siedmiu problemów millenijnych. Co najmniej dwa z nich mają bezpośredni związek z teorią liczb – jak hipoteza Riemanna.
XXI wiek
Nowe tysiąclecie przyniosło między innymi:
- dowód hipotezy Catalana; zrobił to Preda Mihăilescu w 2002 roku;
- twierdzenie Greena-Tao o ciągach arytmetycznych wśród liczb pierwszych.
Ogłoszono też pewne sukcesy, które w lutym 2022 dalej czekają na pełną weryfikację, choć są aktywnie badane przez społeczność akademicką:
- Shinichi Mochizuki w 2012 roku przedstawił pracę, która jego zdaniem dowodzi hipotezy abc;
- Harald Helfgott w 2013 roku zaproponował dowód słabej hipotezy Goldbacha.
W 2018 roku Michael Atiyah ogłosił, że udało mu się udowodnić hipotezę Riemanna i zaprezentował swoją próbę dowodu. Została ona odrzucona przez matematyków jako błędna. Wiele innych problemów teorii liczb – także postawionych elementarnie – w lutym 2022 pozostaje nierozwiązanych. Niektóre z nich to:
- kwestia liczb pierwszych niektórych typów. Nie wiadomo, czy istnieje nieskończenie wiele liczb pierwszych Fibonacciego, Mersenne’a, Germain, bliźniacznych, czworaczych ani czy istnieją jakiekolwiek liczby pierwsze w ciągu Fermata poza pięcioma początkowymi wyrazami. Problem liczb pierwszych Mersenne’a ma konsekwencje dla teorii parzystych liczb doskonałych – nie wiadomo, czy jest ich nieskończenie wiele;
- hipoteza Goldbacha;
- pytania dotyczące liczb całkowitych, ale nie wprost liczb pierwszych, np. prostopadłościan idealny i problem Collatza. Nie wiadomo też, czy istnieje jakakolwiek nieparzysta liczba doskonała ani czy ciąg liczb zaprzyjaźnionych jest skończony;
- wymierność niektórych stałych jak Eulera-Mascheroniego (γ), stałe Feigenbauma (α i δ) czy wartości funkcji dzeta Riemanna dla liczb nieparzystych większych od trzech: ζ(2n+1), n>1. Niektóre problemy dotyczące liczb pierwszych sprowadzono do pytania o wymierność stałych Bruna jak B2 i B4;
- przestępność niektórych liczb niewymiernych jak stała Apéry’ego ζ(3);
- zagadnienia obliczeniowe, np. czy faktoryzacja liczb całkowitych należy do problemów klasy P – tj. czy jej złożoność może być wielomianowa.
Teoria liczb w Polsce

Wśród matematyków polskich znaczące wyniki w teorii liczb uzyskali między innymi:
- Wacław Sierpiński[1] – zob. liczby Sierpińskiego, stała Sierpińskiego;
- Stanisław Ulam – por. spirala Ulama;
- Andrzej Schinzel;
- Henryk Iwaniec – za swoje badania został nagrodzony m.in. Nagrodą Shawa w dziedzinie matematyki (2015);
- Stanisław Knapowski.
Posiadaczem szeregu wyliczeniowych rekordów światowych jest Jarosław Wróblewski. Teorii liczb jest poświęcone polskie czasopismo „Acta Arithmetica”, założone w latach 30. XX w., później wydawane przez Instytut Matematyczny Polskiej Akademii Nauk (IM PAN).
Z polską narodowością i nauką polską bywa też wiązany Franz Mertens – pracownik m.in. Uniwersytetu Jagiellońskiego, zajmujący się analityczną teorią liczb. Jego hipoteza Mertensa, implikująca hipotezę Riemanna, okazała się jednak fałszywa – obalono ją w latach 80. XX w..
Ludzie
Euklides z Aleksandrii (IV w. p.n.e.),
Pierre de Fermat (XVII w.),
Bernhard Riemann (XIX w.),
Do znaczących naukowców w tej dziedzinie należą[1]:
- Euklides z Aleksandrii (IV–III w. p.n.e.)
- Diofantos (III w. n.e.)
- Leonardo Pisano vel Fibonacci (1175–1250)
- Marin Mersenne (1588–1648)
- Pierre de Fermat (1601–1665)
- John Pell (1611–1685)
- Christian Goldbach (1690–1764)
- Leonhard Euler (1707–1783)
- Johann Heinrich Lambert (1728–1777)
- Adrien-Marie Legendre (1752–1833)
- Sophie Germain (1776–1831)
- Carl Friedrich Gauss (1777–1855)
- August Ferdinand Möbius (1790–1868)
- Carl Gustav Jakob Jacobi (1804–1851)
- Peter Gustav Lejeune Dirichlet (1805–1859)
- Gotthold Eisenstein[1],
- Joseph Liouville (1809–1882)
- Ernst Eduard Kummer (1810–1893)
- Eugène Charles Catalan (1814–1894)
- Pafnutij Czebyszow (1821–1894)
- Joseph Louis François Bertrand (1822–1900)
- Leopold Kronecker (1823–1891)
- Bernhard Riemann (1826–1866)
- Richard Dedekind (1831–1916)
- Ferdinand Lindemann (1852–1939)
- David Hilbert (1862–1943)
- Hermann Minkowski (1864–1909)
- Viggo Brun (1882–1978)
- Wacław Sierpiński (1882–1969)
- George Pólya (1887–1985)
- Srinivasa Ramanujan (1887–1920)
- André Weil (1906–1998)
- Hillel Furstenberg (1935–)
- Andrew Wiles (1953–)
- Preda Mihăilescu (1955–)
- Terence Tao (1975–).
Uwagi
- ↑ Liczby kardynalne i porządkowe są badane przez teorię mnogości.
Przypisy
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Liczb teoria, [w:] Encyklopedia PWN [dostęp 2022-02-15].
- ↑ Eric W. Weisstein, Discrete Mathematics, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2022-02-15].
- 1 2 3 Iwaniec 1995 ↓, s. 698.
- ↑ 22·5·7 urodziny, [w:] pismo „Delta”, deltami.edu.pl, marzec 2022, ISSN 0137-3005 [dostęp 2022-03-15] (pol.).
- ↑
 Piotr Sułkowski, Fizyka i teoria liczb, 3 września 2016 [dostęp 2022-02-15].
Piotr Sułkowski, Fizyka i teoria liczb, 3 września 2016 [dostęp 2022-02-15]. - ↑
 Communications in Number Theory and Physics (ang.), intlpress.com [dostęp 2022-02-15].
Communications in Number Theory and Physics (ang.), intlpress.com [dostęp 2022-02-15]. - ↑ Iwaniec 1995 ↓, s. 698–726.
- ↑ Preface, Cambridge University Press, 16 listopada 2006, xi–xii, DOI: 10.1017/cbo9780511618314.001 [dostęp 2023-12-08].
- ↑ Additive number theory: the classical bases, „Choice Reviews Online”, 35 (01), 1997, s. 35–0343-35-0343, DOI: 10.5860/choice.35-0343, ISSN 0009-4978 [dostęp 2023-12-08].
- ↑ Izabella Łaba, From harmonic analysis to arithmetic combinatorics, „Bulletin of the American Mathematical Society”, 45 (01), 2007, s. 77–116, DOI: 10.1090/S0273-0979-07-01189-5, ISSN 0273-0979 [dostęp 2023-12-08] (ang.).
- 1 2 3 Henryk Iwaniec, Emmanuel Kowalski, Analytic Number Theory, „Colloquium Publications”, Providence, Rhode Island: American Mathematical Society, 2004, DOI: 10.1090/coll/053, ISBN 978-0-8218-3633-0 [dostęp 2023-12-08].
- 1 2 D. Goldfeld, The Elementary Proof of the Prime Number Theorem: An Historical Perspective, David Chudnovsky, Gregory Chudnovsky, Melvyn Nathanson (red.), New York, NY: Springer New York, 2004, s. 179–192, DOI: 10.1007/978-1-4419-9060-0_10., isbn, 978-0-387-40655-8., mr, 2044518., ISBN 978-1-4612-6490-3 [dostęp 2023-12-08] (ang.).
- ↑ Zenon I. Borevič, Igorʹ R. Šafarevič, Zenon I. Borevič, Number theory, wyd. 2. [print], Pure and applied mathematics, Orlando: Acad. Pr, 1987, ISBN 978-0-12-117851-2 [dostęp 2023-12-08].
- ↑ MSC2010 database [online], mathscinet.ams.org [dostęp 2023-12-08].
- ↑ Hermann Minkowski, Geometrie der Zahlen, Leipzig-Berlin 1910 (niem.).
- ↑ Gérald Tenenbaum, Gérald Tenenbaum, Introduction to analytic and probabilistic number theory, Cambridge studies in advanced mathematics, Cambridge: Cambridge Univ. Press, 1995, ISBN 978-0-521-41261-2 [dostęp 2023-12-08].
- ↑ Emmanuel Kowalski, An Introduction to Probabilistic Number Theory, Cambridge University Press, 31 marca 2021, DOI: 10.1017/9781108888226, ISBN 978-1-108-88822-6 [dostęp 2023-12-08].
- ↑ Maksym Radziwiłł, Kannan Soundararajan, Selberg’s central limit theorem for log $|\zeta(\tfrac 12+it)|$, „L’Enseignement Mathématique”, 63 (1), 2018, s. 1–19, DOI: 10.4171/lem/63-1/2-1, ISSN 0013-8584 [dostęp 2023-12-08].
- ↑ Ben Green, Book Review: Additive combinatorics, „Bulletin of the American Mathematical Society”, 46 (3), 2009, s. 489–497, DOI: 10.1090/S0273-0979-09-01231-2, ISSN 0273-0979 [dostęp 2023-12-08] (ang.).
- ↑ David Conlon, Jacob Fox, Yufei Zhao, The Green-Tao theorem: an exposition, „EMS Surveys in Mathematical Sciences”, 1 (2), 2014, s. 257–291, DOI: 10.4171/emss/6, ISSN 2308-2151 [dostęp 2023-12-08].
- ↑ Henryk Iwaniec, Emmanuel Kowalski, Analytic Number Theory, t. 53, Providence, Rhode Island: American Mathematical Society, 8 czerwca 2004, DOI: 10.1090/coll/053, ISBN 978-0-8218-3633-0 (ang.).
- 1 2 Iwaniec 1995 ↓, s. 693.
- 1 2 3 Iwaniec 1995 ↓, s. 694.
- ↑ Iwaniec 1995 ↓, s. 720.
- ↑ Iwaniec 1995 ↓, s. 721.
- ↑ Mariusz Skałba, Popularne książki Sierpińskiego, [w:] pismo „Delta”, deltami.edu.pl, marzec 2022, ISSN 0137-3005 [dostęp 2022-03-15] (pol.).
- ↑ Iwaniec 1995 ↓, s. 713.
Bibliografia
- Teoria liczb, [w:] Henryk Iwaniec, Leksykon matematyczny, Warszawa: Wydawnictwo „Wiedza Powszechna”, 1995, ISBN 83-214-0783-8.
Linki zewnętrzne
 Wacław Sierpiński, Teoria liczb, pldml.icm.edu.pl [dostęp 2022-02-16] – monografia z 1950 roku.
Wacław Sierpiński, Teoria liczb, pldml.icm.edu.pl [dostęp 2022-02-16] – monografia z 1950 roku.- Eric W. Weisstein, Number Theory, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-06-01].
 Number theory (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].
Number theory (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].



