1. Prostopadłość prostych w przestrzeni.
Proste prostopadłe na płaszczyźnie to dwie przecinające się proste, z których każda jest osią symetrii drugiej. Proste o tej właściwości są również prostopadłe w przestrzeni. Rozszerzmy jednak pojęcie prostopadłości prostych w przestrzeni, obejmując nim także proste skośne. Skorzystajmy tu z pojęcia wektorów prostopadłych, które jest analogiczne na płaszczyźnie i w przestrzeni.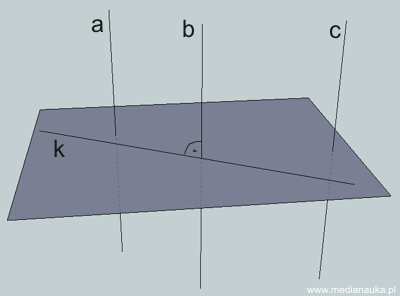
Dwie proste nazywamy prostopadłymi, gdy niezerowe wektory równoległe odpowiednio do każdej z tych prostych są prostopadłe.
Przykład 1. Prosta równoległa do krawędzi bocznej prostopadłościanu jest prostopadła do każdej prostej równoległej do dowolnej krawędzi podstawy.
2. Prostopadłość prostej i płaszczyzny.
Rozważmy dwie płaszczyzny q i r, które przecinają się wzdłuż krawędzi k. Przez punkt O krawędzi k poprowadźmy w płaszczyźnie q prostą a prostopadłą do prostej k, a w płaszczyźnie r - prostą b również prostopadłą do prostej k. Proste a i b przecinają się w punkcie O, więc wyznaczają płaszczyznę p. Prosta k jest zatem prostopadła do dwóch przecinających się prostych, zawartych w płaszczyźnie p.
Twierdzenie:
Jeżeli prosta k jest prostopadła do dwóch przecinających się prostych a i b, to prosta k jest prostopadła do każdej prostej zawartej w płaszczyźnie wyznaczonej przez proste a i b.
Dowód: Z definicji prostopadłości prostych wynika, że prosta k jest prostopadła do każdej prostej równoległej do prostej a lub b. Wystarczy więc, gdy wykażemy, że prosta k jest prostopadła do trzeciej prostej, zawartej w płaszczyźnie p i nierównoległej ani do prostej a, ani do b. Weźmy do rozważań prostą przechodzącą przez punkt O i oznaczmy ją przez c.
Niech wektory OA, OB, OC i OK będą wektorami odpowiednio równoległymi do prostych a, b, c i k. Ponieważ punkty O, A, B i C należą do płaszczyzny p i punkty A, B, O są niewspółliniowe, istnieją takie liczby x i y, że:
\[OC = x \cdot OA + y \cdot OB\]
Na podstawie własności iloczynu skalarnego wektorów, otrzymamy:
\[OK \cdot OC = (x \cdot OA + y \cdot OB) \cdot OK = x \cdot (OK \cdot OA) + y \cdot (OK \cdot OB)\]
Z założenia twierdzenia, wektor OK jest prostopadły do wektorów OA i OB, więc \(OK \cdot OA = 0\) i \(OK \cdot OB = 0\). Stąd otrzymujemy:
\[OK \cdot OC = x \cdot 0 + y \cdot 0 = 0\]
co oznacza, że wektor OK jest prostopadły do wektora OC, czyli prosta k jest prostopadła do prostej c.
W ten sposób wykazaliśmy, że istnieje prosta, która jest prostopadła do każdej prostej zawartej w płaszczyźnie; jest ona jednocześnie prostopadła do każdej prostej równoległej do płaszczyzny.
Prostą nazywamy prostopadłą do płaszczyzny, gdy jest prostopadła do każdej prostej zawartej w płaszczyźnie. Wektor nazywamy prostopadłym do płaszczyzny, gdy jest równoległy do prostej prostopadłej do płaszczyzny.
