| Przemiana izotermiczna charakteryzuje się tym, że T=const i ΔU = 0. Na podstawie I zasady termodynamiki: Q+W=0, czyli: Q= −W. Wniosek: W stałej temperaturze energia wewnętrzna gazu nie zmienia się. Z zasady termodynamiki wynika, że aby to było możliwe, całe dostarczone do gazu ciepło musi być zużyte przez gaz na wykonanie pracy podczas rozprężania się. Z kolei, jeśli gaz jest sprężany (praca jest wykonana nad gazem), to musi całą energię przekazaną mu w ten sposób oddać w postaci ciepła. Praca w przemianie izotermicznej związana jest ze zmianą objętości od V1 do V2. Obliczamy ją według wzoru: 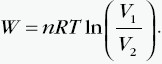 |
W tej przemianie temperatura jest stała, a pozostałe dwa parametry ulegają zmianie zgodnie z prawem Boyle’a-Mariotte’a: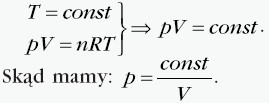 Ciśnienie jest odwrotnie proporcjonalne do objętości gazu, co przedstawia wykres: 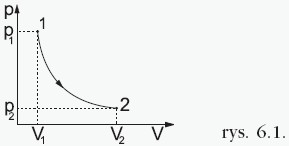 Iloczyn ciśnienia i objętości ustalonej porcji gazu poddanego przemianie izotermicznej jest w każdym stanie gazu taki sam. Przykładowo dla dwóch różnych stanów opisanych przez parametry (p1, V1, T) i (p2, V2, T)mamy: p1 ⋅ V1 = p2 ⋅ V2. |
| Przemiana izochoryczna charakteryzuje się tym, że: V = const oraz W = 0 i ΔU = Q. Wniosek: Przy stałej objętości gazu nie ma sprężania, ani rozprężania gazu. Praca jest wtedy równa zeru, a jedyną przyczyną zmiany energii wewnętrznej jest ciepło wymienione przez gaz z otoczeniem: Q = n ⋅ Cv ⋅ ΔT. Gdy gaz przyjmie ciepło, to jego energia wewnętrzna wzrośnie. Tym samym wzrośnie temperatura gazu, co zgodnie z prawem Charlesa doprowadzi do wzrostu jego ciśnienia. Gdy gaz odda ciepło, jego energia wewnętrzna zmaleje. Oznacza to zmniejszenie temperatury gazu i na podstawie prawa Charlesa, spadek jego ciśnienia. |
W tej przemianie objętość jest stała, a pozostałe dwa parametry zmieniają się zgodnie z prawem Charlesa: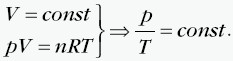 Ciśnienie jest wprost proporcjonalne do temperatury, co przedstawia wykres: 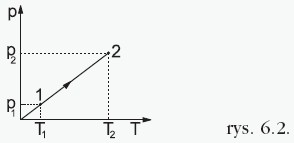 Stosunek ciśnienia do temperatury dla ustalonej porcji gazu poddanego przemianie izochorycznej jest taki sam w każdym stanie tego gazu. Przykładowo dla dwóch różnych stanów opisanych przez parametry (p1, V, T1) i (p2, V, T2) mamy: 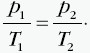 |
| Przemiana izobaryczna charakteryzuje się tym, że: p = const. W ≠ 0, Q ≠ 0 i ΔU=Q+W. Wniosek: Gdy gaz pobiera ciepło (Q > 0) i ma mieć przy tym stałe ciśnienie, to musi się rozprężyć wykonując pracę (W < 0). Na skutek tego wzrośnie jego objętość, co zgodnie z prawem Gay-Lussaca prowadzi do wzrostu temperatury gazu i tym samym do wzrostu jego energii wewnętrznej. Jeśli gaz jest sprężany (W > 0), to zmniejsza się jego objętość. Aby ten proces mógł zachodzić przy stałym ciśnieniu gaz musi oddać ciepło do otoczenia (Q < 0).Wtedy zgodnie z prawem Gay-Lussaca zmniejszeniu objętości towarzyszy spadek temperatury gazu, co oznacza zmniejszenie się energii wewnętrznej. Za każdym razem zmiana energii wewnętrznej jest algebraiczną sumą ciepła wymienionego przez gaz z otoczeniem i pracy. Przy czym: W = p(V1–V2), Q = nCp(T2–T1). |
W tej przemianie ciśnienie gazu jest stałe, a pozostałe dwa parametry zmieniają się zgodnie z prawem Gay-Lussaca: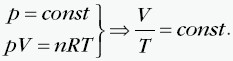 Objętość jest wprost proporcjonalna do temperatury, co przedstawia wykres: 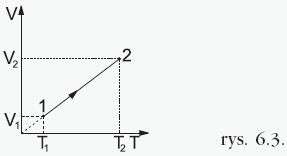 Stosunek objętości do temperatury dla ustalonej porcji gazu poddanego przemianie izobarycznej jest w każdym stanie tego gazu taki sam. Przykładowo dla dwóch różnych stanów opisanych przez parametry(p, V1, T1) i (p, V2, T2) mamy: 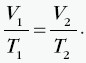 |
| Przemiana adiabatyczna, charakteryzuje się tym, że: Q = 0 i ΔU=W. Wniosek: Gdy gaz jest sprężany adiabatycznie, to zgodnie z prawem Poissona silnie wzrasta ciśnienie gazu, a zgodnie z I zasadą termodynamiki następuje wzrost energii wewnętrznej o wartość równą pracy wykonanej nad gazem: 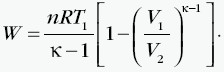 Wzrost energii wewnętrznej jest przyczyną wzrostu temperatury gazu. Jeśli gaz się rozpręży (W < 0), to energia wewnętrzna gazu zmaleje o wartość pracy wykonanej przez gaz, a ciśnienie gazu zmaleje. |
W tej przemianie zmianie ulegają wszystkie trzy parametry stanu gazu zgodnie z równaniem Poissona: gdzie κ – współczynnik adiabatyczny (Poissona) zależny od rodzaju gazu. Zależność ciśnienia od objętości w tej przemianie przedstawia wykres: 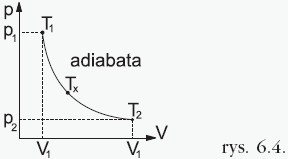 Iloczyn ciśnienia i objętości podniesionej do potęgi dla każdego stanu jednakowej porcji gazu poddanego przemianie adiabatycznej jest taki sam. Przykładowo dla dwóch różnych stanów opisanych przez parametry (p1, V1, T1) i (p2, V2, T2)mamy: p1 ⋅ Vκ1 = p2 ⋅ Vκ2 |
Uwaga: Wszystkie cztery przemiany są procesami odwracalnymi i mogą przebiegać w dwóch, przeciwnych do siebie kierunkach. Od przyjętego kierunku będzie zależało to, kiedy praca i ciepło będą dodatnie, a kiedy ujemne.
