Siła ciężkości (ciężar ciała) na równi pochyłej rozkłada się na dwie siły: siłę równoległą do powierzchni równi –FS i siłę prostopadłą do powierzchni równi –FN Siła FS powoduje ruch ciała wzdłuż równi, a siła FN naciska na równię i dlatego ma wpływ na wartość siły tarcia.
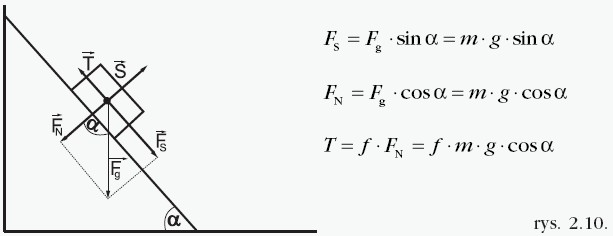
Siła FN jest równoważona przez siłę sprężystości równi S , a niezrównoważona siła wypadkowa o wartości Fws - T = F − nadaje ciału na równi przyspieszenie: 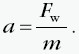
Podstawiając do tego wzoru Fw=FS−T=m⋅g(sinα−f cosα),otrzymujemy wyrażenie na przyspieszenie ciała, które zsuwa się z równi: a=g(sinα−f cosα).
W sytuacji, gdy siłę tarcia można pominąć, czyli f = 0 – przyspieszenie ciała na równi wynosi: a=g⋅sinα.
