Tachionowy antytelefon, znany również jako Paradoks Tolmana – hipotetyczne urządzenie, które można wykorzystać, aby wysłać sygnał w przeszłość. Albert Einstein w 1907 roku^[1] przeprowadził eksperyment myślowy, w którym pokazał, iż sygnały podróżujące z prędkością nadświetlną mogą prowadzić do paradoksów, w których efekt lub konsekwencję wydarzenia można spostrzec przed jego wystąpieniem. Ten sam problem w 1917 roku przedstawił Richard Chase Tolman^[2].

Urządzenie mogące „telegrafować w przeszłość” zostało później nazwane „tachionowym antytelefonem” m.in. przez Gregoryego Benforda^[3]. Dzisiejsze rozumienie fizyki nie dopuszcza możliwości istnienia sygnałów poruszających się z prędkością nadświetlną.

Podróż jednokierunkowa

Problem ten został zilustrowany w 1911 roku przez Paula Ehrenfesta przy użyciu diagramu Minkowskiego. Sygnał zostaje wysłany w układzie B1 z prędkością bliskiej nieskończoności w dwa przeciwne kierunki ON i OP. W tym układzie O następuje przed N. Jednak w innym układzie B2 wydarzenie N następuje przed O^[4].

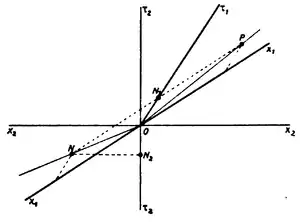
Tolman użył następującej wariacji eksperymentu Einsteina^[2]:

Należy przyjąć, że w przestrzeni istnieją dwa punkty ${\displaystyle A}$ i ${\displaystyle B,}$ które dzieli pewna odległość. Z punktu ${\displaystyle A}$ wysyłany jest sygnał z prędkością ${\displaystyle a}$ w kierunku ${\displaystyle B.}$ Wszystkie pomiary są wykonywane w układzie inercjalnym, gdzie wszystkie punkty są w spoczynku. Czas dostarczenia sygnału do ${\displaystyle B}$ można wyliczyć następująco:

${\displaystyle \Delta t=t_{1}-t_{0}={\frac {B-A}{a}}.}$

W opisanej sytuacji wydarzenie w punkcie ${\displaystyle A}$ jest przyczyną wydarzenia w punkcie ${\displaystyle B.}$ W układzie inercjalnym poruszającym się z prędkością ${\displaystyle v}$ czas dostarczenia sygnału można wyliczyć na podstawie transformacji Lorentza:

${\displaystyle \Delta t'=t'_{1}-t'_{0}={\frac {t_{1}-vB/c^{2}}{\sqrt {1-v^{2}/c^{2}}}}-{\frac {t_{0}-vA/c^{2}}{\sqrt {1-v^{2}/c^{2}}}}={\frac {1-av/c^{2}}{\sqrt {1-v^{2}/c^{2}}}}\Delta t.}$

Jest możliwe udowodnienie, że jeśli ${\displaystyle a>c,}$ to niektóre wartości ${\displaystyle \Delta t}$ mogą być ujemne. Innymi słowy, efekt wydarzenia w punkcie ${\displaystyle A}$ następuje przed powstaniem wydarzenia (wysłany sygnał zostaje dostarczony przed jego wysłaniem).

Zobacz też

• tachion

Przypisy