
Sympleks – uogólnienie odcinka, trójkąta i czworościanu na dowolne wymiary. Intuicyjnie, -wymiarowym sympleksem nazywamy -wymiarowy wielościan, który jest wypukłą otoczką swoich wierzchołków[1].
Definicja w przestrzeni liniowej
Niech
Niech będą wektorami -wymiarowej rzeczywistej przestrzeni liniowej i niech każde różnych wektorów spośród nich tworzą liniowo niezależny układ.
Sympleksem -wymiarowym o wierzchołkach jest zbiór wektorów:
Równoważnie:
Niech
Niech będą wektorami -wymiarowej rzeczywistej przestrzeni liniowej i niech wektory tworzą liniowo niezależny układ.
Sympleksem -wymiarowym jest zbiór wektorów:
Układ wektorów tworzy wierzchołki sympleksu
Definicja w przestrzeni afinicznej
Niech
Niech będą punktami rzeczywistej przestrzeni afinicznej -wymiarowej i niech każde różnych wektorów spośród tworzą liniowo niezależny układ.
Sympleksem -wymiarowym o wierzchołkach jest zbiór punktów:
Zdefiniowany zbiór nie zależy od wyboru punktu
Każdy punkt tak zdefiniowanego sympleksu jest średnią ważoną z wierzchołków o wagach odpowiednio (tzw. kombinacja wypukła).
Sympleks jest najmniejszym wypukłym zbiorem zawierającym punkty
Równoważnie:
Niech
Niech będą punktami rzeczywistej przestrzeni afinicznej -wymiarowej i niech wektory tworzą liniowo niezależny układ.
Sympleksem -wymiarowym o wierzchołkach jest zbiór punktów:
Tak zdefiniowany zbiór nie zależy od sposobu ponumerowania układu punktów
Przestrzeń euklidesowa
- sympleks zerowymiarowy to punkt,
- sympleks jednowymiarowy to odcinek,
- sympleks dwuwymiarowy to trójkąt,
- sympleks trójwymiarowy to czworościan (niekoniecznie foremny),
- sympleks czterowymiarowy to 5-komórka,
i ogólnie:
- sympleks -wymiarowy to wielokomórka, której ścianami jest sympleksów -wymiarowych.
Lista sympleksów
Poniżej znajduje się lista -wymiarowych sympleksów (do włącznie).
| Δn | Grafika (skośny rzut ortogonalny z ang.: skew orthogonal projection) |
Nazwa symbol Schläfliego diagram Coxetera-Dynkina |
Wierzchołków 0-wym. |
Krawędzi 1-wym. |
Ścian 2-wym. |
Komórek 3-wym. |
4-wym. | 5-wym. | 6-wym. | 7-wym. | 8-wym. | 9-wym. | 10-wym. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Δ0 |  |
0-sympleks (punkt) | 1 | ||||||||||
| Δ1 |  |
1-sympleks (odcinek) {} |
2 | 1 | |||||||||
| Δ2 |  |
2-sympleks (trójkąt) {3} |
3 | 3 | 1 | ||||||||
| Δ3 |  |
3-sympleks (czworościan) {3,3} |
4 | 6 | 4 | 1 | |||||||
| Δ4 | 4-sympleks (pentachoron) {3,3,3} |
5 | 10 | 10 | 5 | 1 | |||||||
| Δ5 | 5-sympleks {3,3,3,3} |
6 | 15 | 20 | 15 | 6 | 1 | ||||||
| Δ6 | 6-sympleks {3,3,3,3,3} |
7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||
| Δ7 | 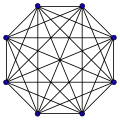 |
7-sympleks {3,3,3,3,3,3} |
8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||
| Δ8 | 8-sympleks {3,3,3,3,3,3,3} |
9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |||
| Δ9 | 9-sympleks {3,3,3,3,3,3,3,3} |
10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | ||
| Δ10 |  |
10-sympleks {3,3,3,3,3,3,3,3,3} |
11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 |
Wielkości opisujące sympleks
Liczba -wymiarowych sympleksów w sympleksie -wymiarowym
Dana jest dwuargumentowa funkcja określająca liczbę sympleksów -wymiarowych w sympleksie -wymiarowym, przy czym Oczywiste jest wówczas, że dowolny sympleks -wymiarowy składa się z:
- sympleksów zerowymiarowych, czyli wierzchołków:
- dokładnie jednego sympleksu -wymiarowego, czyli z samego siebie:
Aby, mając dany -wymiarowy sympleks, utworzyć na jego podstawie sympleks -wymiarowy, należy dodać 1 nowy wierzchołek. Wynika stąd, iż -wymiarowy sympleks będzie miał o 1 wierzchołek więcej, niż sympleks -wymiarowy. Nowe krawędzie (sympleksy jednowymiarowe) dodajemy, łącząc wszystkie wierzchołki pierwotnego sympleksu z nowo utworzonym wierzchołkiem. Tak więc liczba krawędzi w obecnym sympleksie zwiększy się o liczbę wierzchołków w sympleksie pierwotnym. Nowe ściany (sympleksy dwuwymiarowe) tworzymy natomiast, łącząc wszystkie wierzchołki starego sympleksu z nowym wierzchołkiem. Stąd też liczba ścian nowego sympleksu powiększy się o liczbę krawędzi w starym sympleksie itd. Uogólniając powyższe spostrzeżenie na dowolny wymiar: każdy -wymiarowy sympleks posiada pewną liczbę sympleksów -wymiarowych, która jest równa liczbie tych sympleksów dla -wymiarowego sympleksu, powiększoną o liczbę sympleksów -wymiarowych dla tegoż sympleksu. To wszystko zachodzi oczywiście dla
Z powyższych rozważań utworzyć można rekurencyjny wzór na liczbę -wymiarowych sympleksów w dowolnym sympleksie -wymiarowym:
Zauważmy, że gdyby wówczas powyższy wzór opisywałby symbol Newtona, czyli Jednak ponieważ jedynym racjonalnym wzorem, spełniającym wszystkie 3 powyższe warunki wzoru rekurencyjnego, jest Dlatego też ostatecznie wzór jawny na liczbę -wymiarowych sympleksów w dowolnym sympleksie -wymiarowym wyraża się wzorem:
Środek masy sympleksu
- Definicja jawna
Jest to punkt będący średnią arytmetyczną odpowiednich współrzędnych wszystkich wierzchołków -wymiarowego sympleksu:
- Definicja rekurencyjna
Dla sympleksu jednowymiarowego (odcinka) – średnia arytmetyczna odpowiednich współrzędnych obu wierzchołków.
Dla sympleksu -wymiarowego, gdzie – punkt przecięcia się wszystkich środkowych sympleksu, przy czym środkowa sympleksu jest to odcinek łączący dowolny wierzchołek ze środkiem masy sympleksu -wymiarowego przeciwległego do tego wierzchołka.
Środek masy sympleksu foremnego
Dowolny -wymiarowy sympleks foremny można zorientować w -wymiarowym kartezjańskim układzie współrzędnych w taki sposób, aby wartości -tej współrzędnej dla wierzchołków były równe 0, zaś wartość tej współrzędnej dla -tego wierzchołka była różna od 0. Wówczas owe n wierzchołków tworzy pewien -wymiarowy sympleks foremny, będący podstawą naszego sympleksu -wymiarowego, zaś wartość -tej współrzędnej określa jego wysokość. Ponieważ wartości tej współrzędnej wszystkich wierzchołków podstawy wynosi 0, jej wartość dla ich średniej arytmetycznej również wynosi 0. Wynika stąd, iż -ta współrzędna dla środka masy podstawy także ma wartość 0. Jedynie współrzędna ta dla -tego wierzchołka ma wartość różną od 0. W takim razie wartość -tej współrzędnej dla wszystkich wierzchołków jest sumą zer i jednej wartości różnej od zera, podzieloną przez Tak więc wartość tejże współrzędnej dla środka masy naszego -wymiarowego sympleksu jest ilorazem jego wysokości podzieloną przez Ostatecznie, środek danego sympleksu n-wymiarowego położony jest w odległości równej jego wysokości od środka masy jego podstawy i w odległości wynoszącej jego wysokości od wierzchołka przeciwległego do tej podstawy
Wysokość sympleksu foremnego
Biorąc pod uwagę definicję sympleksu foremnego, jego podstawy, jak również i wysokości, udowodnić można prawdziwość poniższej rekurencyjnej zależności pomiędzy wysokością n-wymiarowego sympleksu foremnego a wysokością jego podstawy
Powyższą zależność odpowiednio przekształcamy:
Jako warunek brzegowy tej rekurencyjnej zależności, zakładamy, że wysokość 1-wymiarowego sympleksu foremnego, czyli odcinka, jest równy długości tegoż odcinka, czyli długości krawędzi naszego sympleksu:
Następnie, chcąc policzyć wysokość dowolnego -wymiarowego sympleksu foremnego, podstawiamy do powyższej rekurencyjnej zależności odpowiednio kolejne wartości dla równego od 1 do W wyniku tego otrzymujemy następujący iloczyn:
Upraszczamy możliwie najbardziej powyższe wyrażenie:
Ostatecznie, wysokość -wymiarowego sympleksu foremnego o krawędzi długości wyraża się wzorem:
Natomiast rekurencyjna zależność na tę wysokość:
Nietrudno policzyć, że wysokość sympleksu foremnego o nieskończonej liczbie wymiarów dąży do:
Miara główna sympleksu foremnego
Pod pojęciem miary głównej -wymiarowego sympleksu foremnego rozumieć należy wielkość będącą uogólnieniem długości odcinka, pola powierzchni trójkąta równobocznego oraz objętości czworościanu foremnego, na -ty wymiar. Dowolny -wymiarowy sympleks foremny można podzielić na podstawę, składającą się z n wierzchołków, oraz -tego przeciwległego do tej podstawy wierzchołka. Pomiędzy podstawą a przeciwległym do niej wierzchołkiem istnieje pewna wielkość zwana wysokością sympleksu, która jest równa odległości tego wierzchołka od -wymiarowej hiperpłaszczyzny, w której zawarta jest podstawa. Wysokość sympleksu jest liniowo wprost proporcjonalna do odległości podstawy od przeciwległego do niej wierzchołka. Gdyby połączyć każdy wierzchołek podstawy z wierzchołkiem do niej przeciwległym, wówczas można zauważyć, że nasz -wymiarowy sympleks jest odzwierciedleniem tejże podstawy, znajdującej się w pewnej odległości od jej przeciwległego wierzchołka, w pewnej skali. Ponieważ wszystkie odcinki, uzyskane z połączenia wierzchołków należących do podstawy z przeciwległym do niej wierzchołkiem, są liniami prostymi, skala długości krawędzi podstawy jest liniowo wprost proporcjonalna do jej odległości od jej przeciwległego wierzchołka. Natomiast stosunek skal -wymiarowych miar głównych dwóch podstaw jest równy -szej potędze stosunku długości odpowiednich krawędzi tych podstaw. Wynika więc stąd, iż stosunek skal -wymiarowych miar głównych dwóch podstaw i jest równy -szej potędze stosunku odpowiednich wysokości i łączących te podstawy z przeciwległym do nich wierzchołkiem:
Mnożąc obie strony powyższego równania przez otrzymujemy:
Zakładamy, że pierwsza podstawa jest skalą podstawy naszego n-wymiarowego sympleksu foremnego w zależności od zmiennej z przedziału od 0 do zaś druga podstawa jest podstawą tegoż sympleksu oraz pierwsza wysokość jest zmienną w przedziale od 0 do zaś druga wysokość jest wysokością tego sympleksu:
Wówczas miara główna naszego n-wymiarowego sympleksu foremnego jest całką od 0 do ze skali tego sympleksu w zależności od zmiennej z przedziału od 0 do
Tak więc z powyższego wyrażenia wynika, iż miara główna -wymiarowego sympleksu foremnego jest równa iloczynowi współczynnika miary głównej podstawy tegoż sympleksu oraz jego wysokości, co ma charakter rekurencyjny:
Ze wzoru na wysokość sympleksu foremnego łatwo zauważyć, że wysokość 1-wymiarowego sympleksu foremnego, a więc dla jest równa długości jego krawędzi:
Następnie, chcąc policzyć miarę główną naszego sympleksu, podstawiamy do powyższej rekurencyjnej zależności odpowiednio kolejne wartości dla równego od 1 do W wyniku tego otrzymujemy następujący iloczyn:
Upraszczamy możliwie najbardziej powyższe wyrażenie:
Ostatecznie, miara główna -wymiarowego sympleksu foremnego o krawędzi długości wyraża się wzorem:
Natomiast rekurencyjna zależność na miarę główną naszego sympleksu:
Nietrudno policzyć, że miara główna sympleksu foremnego o nieskończonej liczbie wymiarów dąży do:
Całkowita miara k-wymiarowa sympleksu foremnego n-wymiarowego
Pod pojęciem k-wymiarowej miary całkowitej n-wymiarowego sympleksu foremnego rozumieć należy wielkość będącą uogólnieniem obwodu (całkowitej miary 1-wymiarowej) trójkąta równobocznego (sympleksu foremnego 2-wymiarowego), czworościanu foremnego (sympleksu foremnego 3-wymiarowego) oraz jego pola powierzchni całkowitej (całkowitej miary 2-wymiarowej), odpowiednio na -ty i -ty wymiar. Nietrudno zauważyć, że dowolny -wymiarowy sympleks foremny o krawędzi długości x składa się z jednakowych -wymiarowych sympleksów foremnych, z których długości poszczególnych krawędzi również są równe Tak więc -wymiarowa miara całkowita -wymiarowego sympleksu foremnego o krawędzi długości jest równa iloczynowi miary głównej pojedynczego k-wymiarowego sympleksu foremnego o długości krawędzi, która także wynosi czyli oraz liczby wszystkich takich k-wymiarowych sympleksów foremnych w danym n-wymiarowym sympleksie foremnym
Nietrudno policzyć, że dowolna -wymiarowa miara całkowita sympleksu foremnego o nieskończonej liczbie wymiarów dąży do:
Zobacz też
Przypisy
- ↑ sympleks, [w:] Encyklopedia PWN [dostęp 2021-10-03].
Bibliografia
- Andrzej Białynicki-Birula, Algebra liniowa z geometrią, Warszawa: Wydawnictwo Naukowe PWN, 1976.
- Karol Borsuk, Geometria analityczna wielowymiarowa, t. 23, Warszawa: Państwowe Wydawnictwo Naukowe, 1964 (Biblioteka Matematyczna).
- Jerzy Mioduszewski, Wykłady z topologii. Topologia przestrzeni euklidesowych, Katowice: Wydawnictwo Uniwersytetu Śląskiego, 1994 (Skrypty Uniwersytetu Śląskiego; 501), ISSN 0239-6432.