Funkcja rozkładu prawdopodobieństwa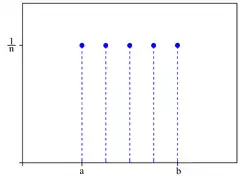 n=5 gdzie n=b-a+1 | |
Dystrybuanta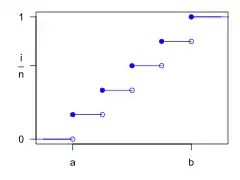 Dystrybuanta dyskretnego rozkładu jednostajnego przy n=5 | |
| Parametry |
|
|---|---|
| Nośnik |
|
| Funkcja rozkładu prawdopodobieństwa |
|
| Dystrybuanta |
|
| Wartość oczekiwana (średnia) |
|
| Mediana |
|
| Moda |
N/A |
| Wariancja |
|
| Współczynnik skośności |
|
| Kurtoza |
|
| Entropia |
|
| Funkcja tworząca momenty |
|
| Funkcja charakterystyczna |
|
Rozkład jednostajny dyskretny (nazywany również równomiernym[1][2]) – dyskretny rozkład prawdopodobieństwa w którym jednakowe prawdopodobieństwo przypisane jest różnym liczbom rzeczywistym a pozostałym liczbom przypisane jest prawdopodobieństwo równe zero[2][3].
Istnieje też wersja ciągła tego rozkładu oraz uogólnienie na dowolne nośniki.
Niektórzy autorzy zakładają dodatkowo[4][5][6], że są wszystkimi liczbami całkowitymi z pewnego przedziału Ta wersja rozkładu przedstawiona jest w ramce z prawej strony.
Przykład: Rozkład wyników rzutu jedną kostką.
Zobacz też
Przypisy
- ↑ Jan Stankiewicz, Katarzyna Wilczek, Elementy rachunku prawdopodobieństwa i statystyki matematycznej: teoria, przykłady, zadania, Matematyka dla Studentów Politechniki Rzeszowskiej, Rzeszów: Oficyna Wydawnicza Politechniki Rzeszowskiej, 2000, s. 141, ISBN 978-83-7199-146-2 [dostęp 2024-02-21].
- 1 2 W. Krysicki i inni, Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, Wydawnictwo Naukowe PWN, 2012, s. 81, ISBN 978-83-01-14293-3 (pol.).
- ↑ Eric W. Weisstein, Discrete Uniform Distribution [online], Wolfram MathWorld [dostęp 2024-02-22] (ang.).
- ↑ http://prac.im.pwr.wroc.pl/~agniesz/rachunek_prawd_MAT1332/files/RPr_MAP1181_rozklady_probabilistyczne.pdf
- ↑ PlanetMath: uniform (discrete) random variable. planetmath.org. [zarchiwizowane z tego adresu (2007-12-11)].
- ↑ Discrete Uniform Distribution. mathsrevision.net. [zarchiwizowane z tego adresu (2008-04-10)].
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.