Potencjał elektrokinetyczny, potencjał dzeta, potencjał zeta, potencjał ζ – potencjał występujący przy powierzchni ciała stałego lub innych cząstek rozproszonych (emulsje), kontaktującej się z roztworem elektrolitu, określany na granicy poślizgu. Granica ta jest powierzchnią oddzielającą tę część przestrzeni międzyfazowej, która zawiera jony unieruchomione na powierzchni fazy stałej i w jej bezpośrednim sąsiedztwie, od jej pozostałej – „rozmytej” – części (zob. podwójna warstwa elektryczna). Istnienie potencjału ζ jest przyczyną występowania zjawisk elektrokinetycznych.
Rodzaje zjawisk elektrokinetycznych
Gdy obie fazy, występujące w układzie faza rozproszona-roztwór elektrolitu, powiązane oddziaływaniami elektrostatycznymi, przemieszczają się lub mogą się przemieszczać względem siebie (zob. kinetyka), obserwowane są efekty nazywane zjawiskami elektrokinetycznymi. Wśród tych zjawisk są wymieniane[1][2][3]:
- powstawanie potencjału między różnymi punktami układu w wyniku wzajemnego przemieszczania się faz:
- powstawanie potencjału przepływu, gdy ciecz przepływa obok nieruchomego ciała stałego (np. różnica potencjałów między punktami po dwóch stronach przegrody lub kapilary, przez którą ciecz jest przetłaczana),
- powstawanie potencjału sedymentacji (efekt Dorna), gdy opadające cząstki ciała stałego (np. cząstek zawiesiny) przemieszczają się względem nieruchomego roztworu (np. różnica potencjałów między krańcowymi punktami kolumny, w której zachodzi sedymentacja),
- ruch faz względem siebie pod wpływem zewnętrznego napięcia:
- ruch cieczy względem nieruchomej fazy stałej – np. proces elektroosmozy (zjawisko odwrotne do powstawania potencjału przepływu),
- przemieszczanie się ciała stałego względem nieruchomej cieczy – np. proces elektroforezy (zjawisko odwrotne do efektu Dorna).
W każdym z tych przypadków wzajemne przemieszczanie się faz zachodzi na „powierzchni ścinania” („powierzchni poślizgu”), znajdującej się wewnątrz cieczy, w pobliżu powierzchni ciała stałego. Powierzchnia ścinania oddziela roztwór zawierający jony silnie przyciągane przez powierzchnię (unieruchomione przy niej siłami adsorpcji i oddziaływania elektrostatycznego) od warstwy ruchomej (nazywanej „rozmytą” lub „dyfuzyjną”[uwaga 1]).

1 – potencjał powierzchni
2 – potencjał Sterna
3 – potencjał dzeta (na granicy poślizgu)
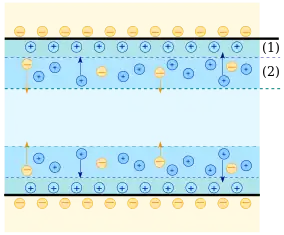
1 – warstwa adsorpcyjna
2 – warstwa dyfuzyjna[uwaga 1]
Podstawy teoretyczne
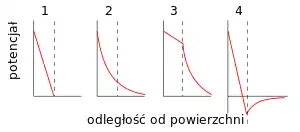
Pierwszy znany model struktury warstwy elektrolitu, kontaktującej się z fazą w nim rozproszoną, zaproponował Hermann von Helmholtz (1879). Potraktował on powierzchnię cząstek fazy rozproszonej i warstwę równoważnej liczby zaadsorbowanych na niej jonów o przeciwnym ładunku jak okładki kondensatora. Konsekwencją tego założenia było stwierdzenie, że potencjał elektryczny w warstwie przypowierzchniowej zmienia się liniowo wraz z odległością. Model zmodyfikowali L.G. Gouy (1909) i D.L. Chapman (1913), Otto Stern (1924) oraz Peter Debye i Erich Hückel (1923). Stwierdzono konieczność uwzględnienia „rozmycia” chmury jonów, znajdujących się w pobliżu naładowanej powierzchni – opisanie zależności potencjału od odległości równaniami nieliniowymi, uwzględniającymi wszystkie rodzaje oddziaływań jonów z powierzchnią oraz z innymi jonami i cząsteczkami w roztworze przypowierzchniowym (w tym siły odpychania cząstek o ładunkach jednoimiennych). Znaczący wkład w badania procesów, zachodzących w przestrzeni przypowierzchniowej, wniósł polski fizyk, Marian Smoluchowski (1872–1917), który – wspólnie z Albertem Einsteinem – opracował teorię dyfuzji, uwzględniającą rolę ruchów Browna[2][4][5].
Dotychczas nie powstał jeden, ogólnie obowiązujący, model przestrzeni międzyfazowej. Przyjmuje się, zgodnie z propozycją Sterna, że w jej ramach można wyodrębnić warstwy o różnych właściwościach – warstwę Helmholtza (adsorpcyjną), w której potencjał zmniejsza się liniowo ze wzrostem odległości, i „warstwę rozmytą”, wewnątrz której przebiega powierzchnia poślizgu[2][6].
Grubość obu części warstwy podwójnej jest rzędu nanometrów. Jest ona zmienna – zależna od składu roztworu i czynników fizycznych – i ściśle związana z wartością długości Debye’a, którą wyraża się jako:
- gdzie:
- – siła jonowa elektrolitu [mol/m³],
- zob. prawo Debye’a-Hückla,
- – przenikalność elektryczna,
- – przenikalność względna,
- – stała Boltzmanna,
- – temperatura absolutna [K],
- – stała Avogadra,
- – ładunek elektryczny elementarny.
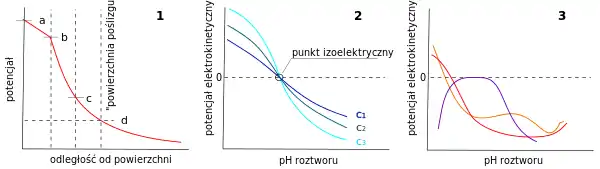
1 – definicja potencjału dzeta (ζ – potencjał w punkcie d), 2 – zależność ζ od pH i stężenia soli oraz punkt izoelektryczny, 3 – zależności ζ od rodzaju cząstek faz rozproszonych i pH (przykłady poglądowe)[2][6]
Potencjał elektrokinetyczny różnych faz rozproszonych zależy w dużym stopniu od stężenia jonów wodorowych. Dla różnych układów koloidalnych istnieje wartość pH, przy której potencjał elektrokinetyczny jest równy zeru (punkt izoelektryczny) i odpychanie elektrostatyczne nie przeciwdziała koagulacji koloidów. Zależność potencjału dzeta od pH i od stężenia innych jonów jest inna dla różnych rodzajów faz rozproszonych, co ilustrują przykłady przedstawione na poglądowym rysunku, opartym na wynikach oznaczeń dzeta kilku rzeczywistych koloidów mineralnych (kopalin)[6].
Obliczanie ζ na podstawie pomiarów
W czasie doświadczalnych oznaczeń wartości potencjałów elektrokinetycznych bywają wykorzystywane wzory Smoluchowskiego w uproszczonej formie, np. w czasie badań opartych na pomiarach[2]:
- prędkości cząstek poruszających się w czasie elektroforezy w cieczy o lepkości w polu o gradiencie potencjału
- objętości cieczy przepływającej w czasie elektroosmozy przez przegrodę o powierzchni pod wpływem gradientu potencjału
Stała jest zależna od kształtu cząstek; przyjmuje się np. że k = 6 w przypadku cząstek kulistych i k = 4 w przypadku cząstek cylindrycznych[2].
Przykładowe wartości
| Faza rozdrobniona | Średnica cząstek [nm] | Potencjał ζ [mV] |
| Emulsja oleju | 2000 | –46 |
| Emulsja parafiny | 724 | –57,4 |
| Zawiesina kwarcu | 1000 | –44 |
| Zawiesina gliny | 1000 | –48,8 |
| Zol złota | ok. 80 | –32 |
| Zol As2S3 | ok. 40 | –32 |
| Zol Fe(OH)3 | ok. 100 | 44 |
Zobacz też
Uwagi
Przypisy
- ↑ Electrokinetic potential, ζ. [w:] International Union of Pure and Applied Chemistry (IUPAC) [on-line]. goldbook.iupac.org. [dostęp 2014-03-01]. (ang.). (pdf).
- 1 2 3 4 5 6 7 Stanisław Bursa: Chemia fizyczna. Wyd. Wyd. 2 popr. Warszawa: Państwowe Wydawnictwo Naukowe, 1979, s. 577–582. ISBN 83-01-00152-6.
- ↑ red. Antoni Basiński: Chemia fizyczna. Warszawa: Państwowe Wydawnictwo Naukowe, 1966, s. 770–771.
- ↑ Marian Smoluchowski: Contribution à la théorie de l’Endosmose électrique et de quelques phénomènes corrélatifs. [w:] Bull. Int. Acad. Sci. Cracovie, 184 [on-line]. 1903. [dostęp 2014-03-01]. (ang.). (pdf).
- ↑ Właściwości kinetyczne układów koloidalnych. [w:] Chemia. Wirtualny podręcznik – podstawy i zastosowania [on-line]. www.chemia.dami.pl. [dostęp 2017-04-18]. [zarchiwizowane z tego adresu (2013-09-10)]. (pol.).
- 1 2 3 Monika Kujawska: Zjawiska elektryczne na granicach faz ciało stałe – roztwór. [w:] Materiały do wykładów z podstaw chemii wzbogacania kopalin [on-line]. Politechnika Śląska. [dostęp 2014-03-02]. (pol.).
Linki zewnętrzne
- Measurement and interpretation of electrokinetic phenomena; 2005 IUPAC, Pure and Applied Chemistry 77, 1753–1805
- Potencjał elektrokinetyczny glebowych cząstek koloidalnych. karnet.up.wroc.pl. [zarchiwizowane z tego adresu (2014-03-02)]. na: karnet.up.wroc.pl
- Józef Stachurski, Ewa Oruba (AGH Kraków, Instytut Przeróbki i Wykorzystania Surowców Mineralnych), Rola potencjału elektrokinetycznego barytu i fluorytu w procesie flotacji Wpływ pH środowiska na potencjał elektrokinetyczny węgli o różnym stopniu wuęglenia na: www.minproc.pwr.wroc.pl
- Tadeusz Fijał, Ewa Małysa, Józef Stachurski (AGH Kraków, Instytut Przeróbki i Wykorzystania Surowców Mineralnych), na: www.minproc.pwr.wroc.pl
- prof. Henryk Galina, Wykład 6 Układy zdyspergowane na: henrykgalina.sd.prz.edu.pl
- Waldemar Nowicki i Grażyna Nowicka, Koagulacja koloidów liofobowych; ćwiczenie 8. Wyznaczenie progu koagulacji hydrozolu złota przez azotan potasowy. staff.amu.edu.pl. [zarchiwizowane z tego adresu (2014-03-02)]. na: www.staff.amu.edu.pl
- Oczyszczanie wody i powietrza > Potencjał Zeta na www.lenntech.pl
- There’s a Malvern instrument for you > Zeta potential na: www.malvern.com
- prof. Marek Kosmulski, Nanocząstki i nanotechnologie na: bc.pollub.pl