Lemat Yonedy – podstawowe narzędzie w wielu zagadnieniach teorii kategorii i w jej zastosowaniach do innych dziedzin matematyki, zwłaszcza do geometrii algebraicznej. Lemat ten dotyczy funktorów reprezentowalnych poprzez funktory główne (zwane też hom-funktorami) i opisuje ogólną postać transformacji naturalnych tych funktorów. Stosuje się go m.in. przy zanurzaniu danej kategorii w kategorię funktorów oraz przy pewnych zagadnieniach jednoznacznej faktoryzacji^{[uwaga 1]}.

Sformułowanie lematu Yonedy

Załóżmy, że ${\displaystyle {\mathfrak {A}}}$ jest kategorią lokalnie małą. Zbiór morfizmów ${\displaystyle X\to Y}$ kategorii ${\displaystyle {\mathfrak {A}}}$ będziemy oznaczać symbolem ${\displaystyle \mathrm {Hom} (X,Y).}$ Symbolem ${\displaystyle \mathrm {Hom} (A,-)}$ oznaczymy kowariantny funktor główny, przyporządkowujący każdemu morfizmowi ${\displaystyle g\colon X\to Y}$ indukowane przekształcenie ${\displaystyle \mathrm {Hom} (A,g)}$ zbioru ${\displaystyle \mathrm {Hom} (A,X)}$ w zbiór ${\displaystyle \mathrm {Hom} (A,Y)}$ określone wzorem ${\displaystyle \mathrm {Hom} (A,g)(\lambda )=g\circ \lambda }$ dla ${\displaystyle \lambda \in \mathrm {Hom} (A,X).}$

Lemat Yonedy^[1][2][3]. Załóżmy, że ${\displaystyle A}$ jest ustalonym obiektem w ${\displaystyle \mathrm {Ob} {\mathfrak {A}},}$ ${\displaystyle F\colon {\mathfrak {A}}\to \mathbf {Set} }$ jest funktorem kowariantnym, a ${\displaystyle \Phi =\{\Phi _{X}\}_{X\in {\mathrm {Ob} }{\mathfrak {A}}}}$ jest transformacją naturalną ${\displaystyle \Phi _{X}\colon {\mathrm {Hom} }(A,X)\to F(X)}$ funktora ${\displaystyle \mathrm {Hom} (A,-)}$ w funktor ${\displaystyle F.}$ Wówczas istnieje dokładnie jeden element ${\displaystyle u\in F(A)}$ taki, że

${\displaystyle \Phi _{X}(f)=F(f)(u)}$ dla ${\displaystyle f\in \mathrm {Hom} (A,X),}$

(1)

gdzie element ${\displaystyle u}$ dany jest wzorem

${\displaystyle u=\Phi _{A}({\mathrm {id} }_{A}).}$

(2)

Odwrotnie, jeśli ${\displaystyle F\colon {\mathfrak {A}}\to \mathbf {Set} }$ jest dowolnym funktorem kowariantnym, ${\displaystyle A\in \mathrm {Ob} {\mathfrak {A}}}$ i określimy element ${\displaystyle u}$ wzorem (2) to (1) wyznacza transformację naturalną ${\displaystyle \Phi _{X}\colon \mathrm {Hom} (A,X)\to F(X).}$ Ponadto przyporządkowanie ${\displaystyle \Phi \leftrightarrow u}$ jest wzajemnie jednoznaczne.

Proof of Yoneda’s lemma

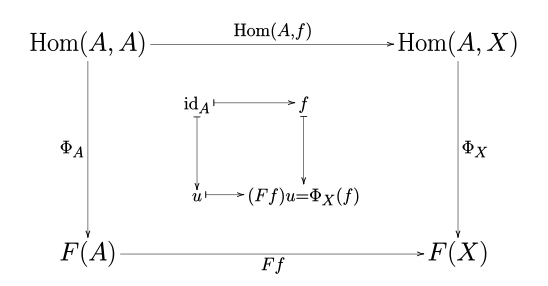
Na powyższym schemacie diagram zewnętrzny ilustruje złożenia morfizmów (jest przemienny na mocy definicji transformacji naturalnej), a diagram wewnętrzny ilustruje przyporządkowania elementów.

Dowód lematu Yonedy polega na bezpośrednim sprawdzeniu ujawniających się tu zależności.

Kontrawariantna wersja lematu Yonedy dotyczy kontrawariantnego funktora głównego ${\displaystyle \mathrm {Hom} (-,A).}$ Rozumowania są analogiczne.

Uwagi

Przypisy

Bibliografia

• Zbigniew Semadeni, Antoni Wiweger: Wstęp do teorii kategorii i funktorów. Wyd. 2. T. 45. Warszawa: Państwowe Wydawnictwo Naukowe, 1978, seria: Biblioteka Matematyczna.
• Saunders Mac Lane: Categories for the working mathematician. Berlin Heidelberg New York: Springer Verlag, 1971. ISBN 3-540-90036-5.

Linki zewnętrzne

• Marek Zawadowski, Elementy teorii kategorii, skrypt dla studentów Wydziału MIM UW, 29 listopada 2019 [dostęp 2021-08-17].