Fold (z ang. składać, zwijać) to rodzina funkcji wyższego rzędu występująca w językach funkcyjnych. Znana jest również jako reduce, accumulate, compress bądź inject. Funkcje fold przetwarzają uporządkowane kolekcje danych (zazwyczaj listy) w celu zbudowania końcowego wyniku przy pomocy jakiejś funkcji łączącej elementy. Dwie najbardziej popularne funkcje z tej rodziny to foldr (fold right) i foldl (fold left).
Funkcje fold są w pewnym sensie dualne do funkcji z rodziny unfold, które z pojedynczej wartości oraz zadanej funkcji generują kolekcję danych. Fold zaś z kolekcji danych, przy pomocy zadanej funkcji, generuje pojedynczy wynik. Oba procesy znane są pod nazwami anamorfizm i katamorfizm.
Funkcje fold na listach
Zastosowanie funkcji z rodziny fold na liście [1,2,3,4,5], wraz z operatorem dodawania da wynik 15, czyli sumę wszystkich elementów tej listy. Do pewnego stopnia fold na liście działa tak, jakby zastępował przecinki zadanym operatorem. W omawianym tu przypadku, rezultatem byłoby 1+2+3+4+5.
W powyższym przykładzie nie użyto nawiasów, lecz dla operatora dodawania (który jest łączny) nie ma to znaczenia. Jednakże w przypadku wielu funkcji, chociażby odejmowania, fakt rozmieszczenia nawiasów, a przez to kolejności wykonywania operacji, ma istotne znaczenie. Dwa podstawowe podejścia do problemu to łączenie rekurencyjnie od pierwszego elementu (określane jako prawy fold czyli foldr), oraz rekurencyjne łączenie elementów rozpoczynając od ostatniego (lewy fold, czyli foldl). W naszym przykładzie foldr ustawiłby nawiasy w następujący sposób: 1 + (2 + (3 + (4 + 5))). Dla foldl ustawienie nawiasów byłoby następujące: (((1 + 2) + 3) + 4) + 5.
Dotychczas mowa była tylko o dwóch parametrach początkowych dla funkcji z rodziny fold, ale często podaje się również trzeci argument: wartość początkową, do której dołączane są elementy listy. Jeżeli w powyższym przykładzie jako wartość początkową ustawiono by liczbę 0, foldr wykonałby działania zgodnie z notacją 1 + (2 + (3 + (4 + (5 + 0)))), zaś foldl: ((((0 + 1) + 2) + 3) + 4) + 5.
Zwijanie list jako operacja strukturalna
Jak już było wspomniane, funkcje fold mogą działać na zasadzie przypominającej zamianę przecinków na operatory. W rzeczywistości jest to bliższe zamianie komponentów tworzących strukturę funkcjami i wartościami, postępując w uporządkowany odgórnie sposób.
W większości języków programowania lista jest albo listą pustą (w informatyce najczęściej oznaczaną przez nil), bądź też jest to wynik dołączenia pewnego elementu do końca istniejącej listy (oznaczane zwykle jako cons). W języku Haskell lista pusta oznaczana jest jako [], zaś operacja cons oznaczana jest symbolem (:) (dwukropek). W takim zapisie lista [1,2,3,4,5] ma postać: 1:2:3:4:5:[]. Wówczas można spojrzeć na funkcję foldr jako formę „zamiany” nil na końcu listy wartością początkową, zaś operacji cons – konkretną funkcją. Najprościej ilustruje to poniższy diagram:
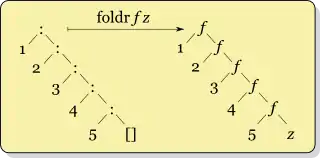
Dla foldl wartość początkowa zastąpiłaby nil umieszczony na początku listy, co prezentuje kolejny diagram:
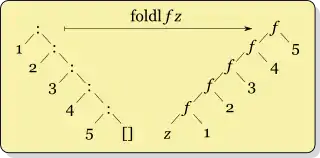
Diagramy te ilustrują również pochodzenie słów „lewy” i „prawy” fold. Można również zaobserwować, że wywołanie foldr (:) [] to funkcja identycznościowa na liście, każda lista przekazana jako parametr do tego wywołania, zostanie zwrócona jako wynik w niezmienionym kształcie.
Implementacja
W Haskellu funkcje foldr i foldl mogą być zapisane w postaci kilku równań:
foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)
W powyższym przykładzie jeżeli lista wejściowa jest pusta, wynikiem jest wartość początkowa, w przeciwnym przypadku wywołaj funkcję f na pierwszym elemencie listy i na wyniku rekurencyjnego wywołania foldr.
foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs
W powyższym przykładzie jeżeli lista wejściowa jest pusta, wynikiem jest wartość początkowa, w przeciwnym przypadku wywołaj foldl z nową wartością początkową powstałą z wywołania funkcji f na poprzedniej wartości początkowej oraz na pierwszym elemencie listy.
W języku Scheme oraz innych pochodnych Lispa pustą listę, oraz operator składania listy reprezentuje się oznaczeniami: () oraz cons. Prawy i lewy fold w języku Scheme mają następujące implementacje, odpowiednio:
(define (foldr f z xs)
(if (null? xs)
z
(f (car xs) (foldr f z (cdr xs)))))
oraz
(define (foldl f z xs)
(if (null? xs)
z
(foldl f (f (car xs) z) (cdr xs))))
Gdzie null? oznacza funkcję predykatów zwracającą prawdę, gdy argumentem dla niej jest lista pusta.
| Language | Lewy fold | Prawy fold | Lewy fold 1[1] | Prawy fold 1[1] | Uwagi |
|---|---|---|---|---|---|
| Haskell | foldl func initval list | foldr func initval list | foldl1 func list | foldr1 func list | |
| OCaml | List.fold_left func initval list Array.fold_left func initval array |
List.fold_right func list initval Array.fold_right func array initval |
|||
| OZ | {FoldL List Func Initval} | {FoldR List Func Initval} | |||
| Python 2.x | reduce(func, list, initval) | reduce(lambda x,y: func(y,x), reversed(list), initval) | reduce(func, list) | reduce(lambda x,y: func(y,x), reversed(list)) | |
| Python 3.x | functools.reduce(func, list, initval) | functools.reduce(lambda x,y: func(y,x), reversed(list), initval) | functools.reduce(func, list) | functools.reduce(lambda x,y: func(y,x), reversed(list)) | reduce jest pakiecie functools. Żeby używać functools.reduce: import functools |
| Ruby | enum.inject(initval) { block } enum.reduce(initval) { block } |
enum.reverse_each.inject(initval, block) enum.reverse_each.reduce(initval, block) |
enum.inject { block } enum.reduce { block } |
enum.reverse_each.inject(block) enum.reverse_each.reduce(block) |
W Ruby 1.8.7+, można podawać również symbol oznaczający funkcję zamiast bloku enum to Enumerator |
| C++ | std::accumulate(begin, end, initval, func) | std::accumulate(rbegin, rend, initval, func) | w nagłówku <numeric> begin i end to iteratory | ||
| Perl | reduce block initval, list | reduce block list | w module List::Util | ||
| C# 3.0 | ienum.Aggregate(initval, func) | ienum.Reverse().Aggregate(initval, func) | ienum.Aggregate(func) | ienum.Reverse().Aggregate(func) | Aggregate jest rozszerzeniem typu ienum jest typu IEnumerable Konstrukcja analogiczna dla pozostałych języków .NET |
| Java 8+ | stream.reduce |
stream.reduce |
|||
| JavaScript 1.8 | array.reduce(func, initval) | array.reduceRight(func, initval) | array.reduce(func) | array.reduceRight(func) | |
| Common Lisp | (reduce func list :initial-value initval) | (reduce func list :from-end t :initial-value initval) | (reduce func list) | (reduce func list :from-end t) | func to symbol |
| Scheme R6RS | (fold-left func initval list) | (fold-right func initval list) | |||
| Smalltalk | collection inject: value into: [ :value :each | ... ] | ||||
| Erlang | lists:foldl(Fun, Accumulator, List) | lists:foldr(Fun, Accumulator, List) | |||
| PHP | array_reduce(array, func, initval) | array_reduce(array, func) | initval czyli wartość początkowa może być jedynie typu integer. Kiedy nie ma initval używany jest NULL, więc nie jest to wersja foldl1. | ||
| Scala | list.foldLeft(initval)(func) | list.foldRight(initval)(func) | list.reduceLeft(func) | list.reduceRight(func) | |
| Mathematica | Fold[func, initval, list] | Fold[func, initval, Reverse[list]] | Fold[func, list] | Fold[func, Reverse[list]] | Fold bez wartości początkowej jest obsługiwany dla wersji 10.0 i wyższej |
| Maple | foldl(func, initval, sequence) | foldr(func, initval, sequence) | |||
| Julia[2] | foldl(op, itr; [init]) | foldr(op, itr; [init]) | foldl(op, itr) | foldr(op, itr) |
Kolejność ewaluacji
Jeżeli w języku występuje leniwa ewaluacja, foldr od razu zwróci wynik wywołania funkcji f na rekurencyjnym wołaniu foldr. Przy czym jeżeli f może obliczyć wynik nie korzystając z wyniku wewnętrznej rekurencji, nie będzie ona przetwarzana i rekurencja ogólna ulegnie zatrzymaniu. Z tego powodu foldr można wywoływać na nieskończonych listach. Z drugiej strony foldl na listach nieskończonych uległby zapętleniu.
Kolejną kwestią, która pojawia się przy leniwej ewaluacji lewych foldów, jest to, że wartość początkowa nie jest obliczana, zanim nie zostanie wywołana rekurencja. Może to doprowadzić do przepełnienia stosu, jeżeli po przejrzeniu długiej listy trzeba jeszcze obliczyć wielkie wyrażenie. Z tego powodu niektóre języki wprowadzają ograniczenia na foldl wymuszające ewaluację wartości początkowej przed przystąpieniem do rekurencji. W języku Haskell taką funkcjonalność realizuje foldl' (gdzie apostrof oznacza prime) dostępna w bibliotece Data.List.
W sytuacji, gdy nie znamy elementu neutralnego funkcji f, bądź chcemy aby operacja wykonywana była jedynie na elementach zadanej listy, bez dodatkowej wartości początkowej, wówczas mamy do dyspozycji odmiany foldr i foldl. Foldr1 i foldl1 używają odpowiednio ostatniego i pierwszego elementu listy w miejsce wartości początkowej. 1 w nazwie odnosi się m.in. do minimalnej wielkości listy (przynajmniej 1 element).
Przykłady
Odwrócenie listy:
rev = foldl (\ys x -> x : ys) [] -- Haskell
(reduce (fn [ys x] (cons x ys)) () coll) ; Clojure
gdzie (\ys x -> x : ys) i (fn [ys x] (cons x ys)) to funkcje, które zwracają listę ys z elementem x na początku.
map f = foldr ((:) . f) [] -- Haskell
(defn map [f coll] (reduce
(fn [ys x] (cons (f x) ys)) () (reverse coll))) ; Clojure
gdzie kropka (.) to operator składania funkcji, a dwukropek (:) to tworzenie listy (cons). Clojure nie posiada funkcji reduce-right/foldr, ale wywołanie reverse przynosi ten sam efekt.
Złączenie napisów, aby uzyskać: "(f 1 (f 2 (f 3 (f 4 (f 5 z)))))"
foldr (\x y -> concat ["(f ",x," ",y,")"]) "z" ["1","2","3","4","5"]
Złączenie napisów, aby uzyskać: "(f (f (f (f (f z 1) 2) 3) 4) 5)"
foldl (\x y -> concat ["(f ",x," ",y,")"]) "z" ["1","2","3","4","5"]
Zobacz też
Przypisy
- 1 2 „Lewy fold 1” oraz „prawy fold 1” to odmiany odpowiednich foldów, które nie pobierają wartości początkowej jako argumentu. Pierwsza wykonywana operacja pobiera jako argumenty dwa pierwsze elementy listy. Z tego powodu nie można tych odmian stosować na listach pustych, zaś typ funkcji łączącej ograniczony jest do
(a, a) -> a, co oznacza, że oba argumenty oraz wynik muszą być tego samego typu. Obie odmiany mają swoje zastosowania np. przy konkatenacji napisów. - ↑ Collections and Data Structures · The Julia Language [online], docs.julialang.org [dostęp 2023-06-09].
Linki zewnętrzne
- Przykłady wywołań funkcji fold w Haskellu
- "Funkcje wyższego rzędu — map, fold i filter"
- "Unit 6: The Higher-order fold Functions". cs.bham.ac.uk. [zarchiwizowane z tego adresu (2009-03-16)].
- "Opis funkcji fold"
- Różnice pomiędzy foldr a foldl.
- "Constructing List Homomorphism from Left and Right Folds"
- "The magic foldr". caos.di.uminho.pt. [zarchiwizowane z tego adresu (2008-10-21)].