The Mathematics Portal
Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)
Featured articles –
Selected image –
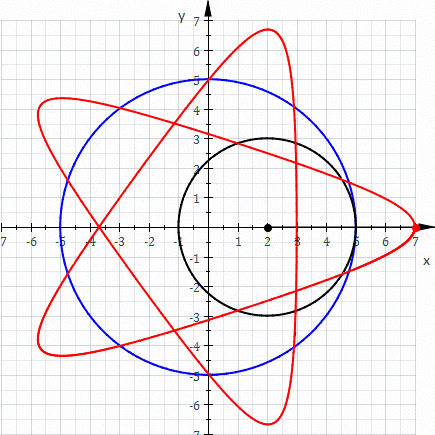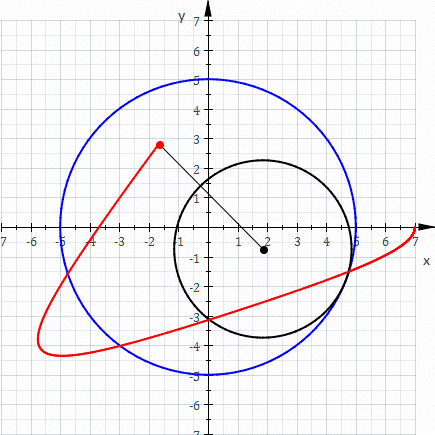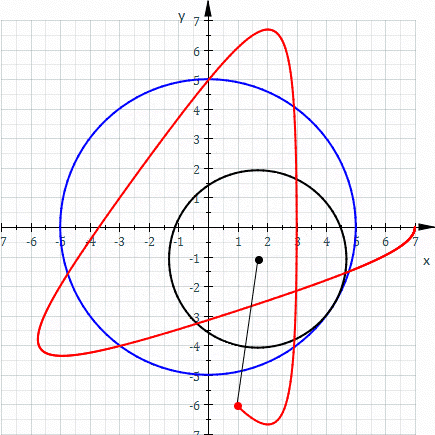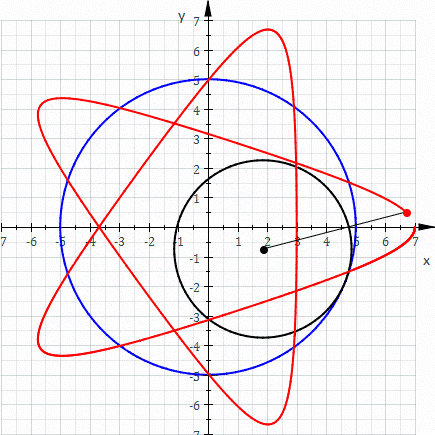
Good articles –
Did you know (auto-generated) –
- ... that the mathematical infinity symbol ∞ may be derived from the Roman numerals for 1000 or for 100 million?
- ... that 100 years after Mary Emily Sinclair wrote a master's thesis in mathematics on the discriminants of quintic polynomials, Helaman Ferguson based a sculpture on her work?
- ... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?
- ... that an equivalence between algebraic and geometric definitions of constructible numbers helps prove the impossibility of squaring the circle?
- ... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
- ... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
- ... that Donn Piatt threw his mathematics teacher out of the window?
- ... that the prologue to The Polymath was written by Martin Kemp, a leading expert on Leonardo da Vinci?
More did you know –

- ...that in Floyd's algorithm for cycle detection, the tortoise and hare move at very different speeds, but always finish at the same spot?
- ...that in graph theory, a pseudoforest can contain trees and pseudotrees, but cannot contain any butterflies, diamonds, handcuffs, or bicycles?
- ...that it is not possible to configure two mutually inscribed quadrilaterals in the Euclidean plane, but the Möbius–Kantor graph describes a solution in the complex projective plane?
- ...that the six permutations of the vector (1,2,3) form a hexagon in 3D space, the 24 permutations of (1,2,3,4) form a truncated octahedron in four dimensions, and both are examples of permutohedra?
- ...that the Rule 184 cellular automaton can simultaneously model the behavior of cars moving in traffic, the accumulation of particles on a surface, and particle-antiparticle annihilation reactions?
- ...that a cyclic cellular automaton is a system of simple mathematical rules that can generate complex patterns mixing random chaos, blocks of color, and spirals?
- ...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
Selected article –
 |
| The four charts each map part of the circle to an open interval, and together cover the whole circle. Image credit: User:KSmrq |
A manifold is an abstract mathematical space in which every point has a neighborhood which resembles Euclidean space, but in which the global structure may be more complicated. In discussing manifolds, the idea of dimension is important. For example, lines are one-dimensional, and planes two-dimensional.
In a one-dimensional manifold (or one-manifold), every point has a neighborhood that looks like a segment of a line. Examples of one-manifolds include a line, a circle, and two separate circles. In a two-manifold, every point has a neighborhood that looks like a disk. Examples include a plane, the surface of a sphere, and the surface of a torus.
Manifolds are important objects in mathematics and physics because they allow more complicated structures to be expressed and understood in terms of the relatively well-understood properties of simpler spaces. (Full article...)
| View all selected articles |
Subcategories
Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming
Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems
Topics in mathematics
| General | Foundations | Number theory | Discrete mathematics |
|---|---|---|---|
| |||
| Algebra | Analysis | Geometry and topology | Applied mathematics |
Index of mathematics articles
| ARTICLE INDEX: |
|
| MATHEMATICIANS: |
|
Related portals
WikiProjects
![]() The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.
The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.
|
Project pages
Essays
Subprojects
Related projects Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics
|
Things you can do
|
In other Wikimedia projects
The following Wikimedia Foundation sister projects provide more on this subject:
-
 Commons
Commons
Free media repository -
 Wikibooks
Wikibooks
Free textbooks and manuals -
 Wikidata
Wikidata
Free knowledge base -
 Wikinews
Wikinews
Free-content news -
 Wikiquote
Wikiquote
Collection of quotations -
 Wikisource
Wikisource
Free-content library -
 Wikiversity
Wikiversity
Free learning tools -
 Wiktionary
Wiktionary
Dictionary and thesaurus
More portals
-
 List of all portals
List of all portals -

-

-

-

-

-

-
-

-

-
 Random portal
Random portal -
 WikiProject Portals
WikiProject Portals
- ↑ Coxeter et al. (1999), p. 30–31; Wenninger (1971), p. 65.

![Image 1Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)](../I/Blank.png.webp)














