Ibn al-Shatir
Ibn al-Shatir's lunar model.
Born1304
Damascus
Died1375 (aged 71)
OccupationAstronomer
Workskitab nihayat al-sul fi tashih al-usul

ʿAbu al-Ḥasan Alāʾ al‐Dīn bin Alī bin Ibrāhīm bin Muhammad bin al-Matam al-Ansari[1] known as Ibn al-Shatir or Ibn ash-Shatir (Arabic: ابن الشاطر; 1304–1375) was an Arab astronomer, mathematician and engineer. He worked as muwaqqit (موقت, religious timekeeper) in the Umayyad Mosque in Damascus and constructed a sundial for its minaret in 1371/72.

Biography

Ibn al-Shatir was born in Damascus, Syria around the year 1304. His father died when he was six years old. His grandfather took him in which resulted in Ibn al-Shatir learning the craft of inlaying ivory.[2] Ibn al-Shatir traveled to Cairo and Alexandria to study astronomy, where he fell in, inspired him.[2] After completing his studies with Abu ‘Ali al-Marrakushi, Ibn al-Shatir returned to his home in Damascus where he was then appointed muwaqqit (timekeeper) of the Umayyad Mosque.[2] Part of his duties as muqaqqit involved keeping track of the times of the five daily prayers and when the month of Ramadan would begin and end.[3] To accomplish this, he created a variety of astronomical instruments. He made several astronomical observations and calculations both for the purposes of the mosque, and to fuel his later research. These observations and calculations were organized in a series of astronomical tables.[4] His first set of tables, which have been lost over time, allegedly combined his observations with those of Ptolemy, and contained entries on the Sun, Moon and Earth.[3]

Astronomy

Ibn al-Shatir most important astronomical treatise was kitab nihayat al-sul fi tashih al-usul ("The Final Quest Concerning the Rectification of Principles"). In it he drastically reformed the Ptolemaic models of the Sun, Moon and planets. His model incorporated the Urdi lemma, and eliminated the need for an equant (a point on the opposite side of the center of the larger circle from the Earth) by introducing an extra epicycle (the Tusi-couple), departing from the Ptolemaic system in a way that was mathematically identical (but conceptually very different) to what Nicolaus Copernicus did in the 16th century. This new planetary model was published in his work the al-Zij al-jadid (The New Planetary Handbook.)[3] Before the kitab nihayat al-sul fi tashih al-usul was made, there was a treatise that Ibn al-Shatir made which described the observations and procedures that lead to him creating his new planetary models.[3]

Unlike previous astronomers before him, Ibn al-Shatir was not concerned with adhering to the theoretical principles of natural philosophy or Aristotelian cosmology, but rather to produce a model that was more consistent with empirical observations and contemporary theory. For example, it was Ibn al-Shatir's concern for observational accuracy which led him to eliminate the epicycle in the Ptolemaic solar model and all the eccentrics, epicycles and equant in the Ptolemaic lunar model. Shatir's new planetary model consisted of new secondary epicycles instead of equant, which improved on the Ptolemaic model. His model was thus in better agreement with empirical observations than any previous model,[5] and was also the first that permitted empirical testing.[6] His work thus marked a turning point in astronomy, which may be considered a "Scientific Revolution before the Renaissance".[5]

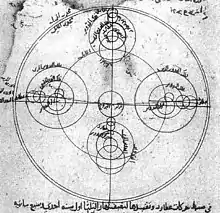
Ibn al-Shatir's model for the appearances of Mercury, showing the multiplication of epicycles in a Ptolemaic enterprise

Drawing on the observation that the distance to the Moon did not change as drastically as required by Ptolemy's lunar model, Ibn al-Shatir produced a new lunar model that replaced Ptolemy's crank mechanism with a double epicycle model that reduced the computed range of distances of the Moon from the Earth.[7] This was the first accurate lunar model which matched physical observations.[8]

Solar Model

Ibn al-Shatir's Solar Model exemplifies his commitment towards accurate observational data, and its creation serves as a general improvement towards the Ptolemaic model. When observing the Ptolemaic solar model, it is clear that most of the observations are not accounted for, and cannot accommodate the observed variations of the apparent size of the solar diameter.[9] Because the Ptolemaic system contains some faulty numerical values for its observations, the actual geocentric distance of the Sun had been greatly underestimated in its solar model. And with the problems that had arisen from the Ptolemaic models, there was an influx of need to create solutions that would resolve them. Ibn al-Shatir's model aimed to do just that, creating a new eccentricity for the solar model. And with his numerous observations, Ibn al-Shatir was able to generate a new maximum solar equation (2;2,6°), which he found to have occurred at the mean longitude λ 97° or 263° from the apogee.[10] As the method was deciphered through geometric ways, it was easy to identify that 7;7 and 2;7 were the radii of the epicycles.[11] In addition, his final results for apparent size of the solar diameter were concluded to be at apogee (0;29,5), at perigee (0;36,55), and at mean distance (0;32.32).[10] This was partially done by reducing Ptolemy’s circular geometric models to numerical tables in order to perform independent calculations to find the longitude of the planets.[1] The longitude of the planets was defined as a function of the mean longitude and the anomaly. Rather than calculating every possible value, which would be difficult and labor-intensive, four functions of a single value were calculated for each planet and combined to calculate quite accurately the true longitude of each planet.[12]

To calculate the true longitude of the moon, Ibn al-Shatir assigned two variables, η, which represented the Moon's mean elongation from the Sun, and γ, which represented its mean anomaly. To any pair of these values was a corresponding e, or equation which was added to the mean longitude to calculate the true longitude. Ibn al-Shatir used the same mathematical scheme when finding the true longitudes of the planets, except for the planets the variables became α, the mean longitude measured from apogee (or the mean center) and γ which was the mean anomaly as for the moon. A correcting function c3' was tabulated and added to the mean anomaly γ to determine the true anomaly γ'.[12] As shown in Shatir's model, it was later discovered that Shatir's lunar model had a very similar concept as Copernicus.[2] Ibn al-Shatir never gave motivation towards his two epicycles to be adopted, so it was hard to tell the difference between his model and the Ptolemaic model.

Possible influence on Nicolaus Copernicus

Although Ibn al-Shatir's system was firmly geocentric (he had eliminated the Ptolemaic eccentrics), the mathematical details of his system were identical to those in Copernicus's De revolutionibus.[13] Furthermore, the exact replacement of the equant by two epicycles used by Copernicus in the Commentariolus paralleled the work of Ibn al-Shatir one century earlier.[14] Ibn al-Shatir's lunar and Mercury models are also identical to those of Copernicus.[15] Copernicus's Mercury model was flawed in the fact that he was not able to properly understand the model first created by Ibn al-Shatir. Copernicus also translated Ptolemy's geometric models to longitudinal tables in the same way Ibn al Shatir did when constructing his solar model.[1] This has led some scholars to argue that Copernicus must have had access to some yet to be identified work on the ideas of Ibn al-Shatir.[16] It is unknown whether Copernicus read Ibn al-Shatir and the argument is still debated. The differences between the two can be seen in their works. Copernicus followed a heliocentric model (planets orbit the Sun) while Ibn al-Shatir followed the geocentric model (as mentioned earlier). Also Copernicus followed the inductive reasoning while Ibn al-Shatir followed the Zij traditions.[15] A Byzantine manuscript containing a solar model diagram with a second epicycle, was discovered to have been in Italy at the time of Copernicus. The presence of this eastern manuscript containing the ideas of Islamic scholars in Italy provides potential evidence of transmission of astronomical theories from the East to Western Europe.[17]

Instruments

The idea of using hours of equal time length throughout the year was the innovation of Ibn al-Shatir in 1371, based on earlier developments in trigonometry by al-Battānī. Before the Islamicate scholar created the improved sundial, he had to understand the sundial created by his predecessors. The Greek had sundials too, but they had nodus-based with straight hour lines which meant that the hours in the day would be unequal (temporary hours) depending on the season. Each day was split into twelve equal segments which meant that the hours would have been shorter in the winter and longer in the summer due to the activity of the sun.[18] Ibn al-Shatir was aware that "using a gnomon that is parallel to the Earth's axis will produce sundials whose hour lines indicate equal hours on any day of the year." His sundial is the oldest polar-axis sundial still in existence. The concept later appeared in Western sundials from at least 1446.[18][19]

Ibn al-Shatir also invented a timekeeping device called "Sandūq al‐Yawāqīt li maʿrifat al-Mawāqīt" (jewel box), which incorporates both a universal sundial and a magnetic compass. He invented it for the purpose of finding the times of prayers.[20] The "Sandūq al‐Yawāqīt li maʿrifat al-Mawāqīt" had a moveable hole in it which allowed the user to find the hour angle of the sun. If this angle was suitable with the horizon, then the user could use it as a polar sundial.[21] This device is preserved in the museum of Aleppo (largest museum in the city of Aleppo, Syria).[21] He also created a sundial which was placed on top of the Madhanat al-Arus (The Minaret of the Bride) in the Umayyad Mosque.[13] The sundial was created on a slab of marble which was approximately 2 meters by 1 meter. The sundial being engraved on the marble was so that Ibn al-Shatir could read the time of the day in equinoctial (equal times) hours for the prayer times.[13] This sundial was later removed in the eighteenth century and a replica was put in its place. The original sundial was placed in the Damascus archeology museum.[21] He also created another sundial but in smaller dimensions (12 cm x 12 cm × 3 cm) to find out the prayer times of midday and the afternoon. This sundial was able to tell the local meridian and the direction of the mecca (located in Saudi Arabia).[21] Other notable instruments invented by him include a reversed astrolabe and an astrolabic clock.[22] The astrolabe that he created was called the al‐āla al‐jāmiʿa (the universal instrument). This astrolabe was created by Ibn al-Shatir when he wrote on the ordinary planispheric astrolabe and when he wrote on the two most common quadrants (the astrolabic and the trigonometric varieties).[22] These two common quadrants were modified versions of the sine quadrant. He also created a set of tables that had values of spherical astronomical functions for prayer times. The tables displayed the times for the morning, afternoon, and evening prayers. The latitude that was used to create the table was 34° (which was correspondent to a location north of Damascus).[4]

See also

Notes

  1. 1 2 3 Roberts, Victor (1966). "The Planetary Theory of Ibn al-Shatir: Latitudes of the Planets". Isis. 57 (2): 208–219. doi:10.1086/350114. JSTOR 227960. S2CID 143576999.
  2. 1 2 3 4 Freely, John (2015). Light from the East: how the Science of Medieval Islam helped to shape the Western World. I.B. Tauris. ISBN 978-1784531386.
  3. 1 2 3 4 Freely, John. (2010). Light from the East : How the Science of Medieval Islam helped to shape the Western World. London: I.B. Tauris. ISBN 978-0-85772-037-5. OCLC 772844807.
  4. 1 2 Abbud, Fuad (December 1962). "The Planetary Theory of Ibn al-Shatir: Reduction of the Geometric Models to Numerical Tables". Isis. 53 (4): 492–499. doi:10.1086/349635. ISSN 0021-1753. S2CID 121312064.
  5. 1 2 (Saliba 1994b, pp. 233–234 & 240)
  6. ↑ Y. M. Faruqi (2006). "Contributions of Islamic scholars to the scientific enterprise", International Education Journal 7 (4): 395–396.
  7. ↑ Neugebauer (1975), volume 3 at pages 1108–1109.
  8. ↑ Morris, T. J. (13 September 2012). A Paranormal History Guide. Lulu.com. ISBN 9781300192459.
  9. ↑ Saliba, George (1987). "Theory and Observation in Islamic Astronomy: The Work of IBN AL-SHĀTIR of Damascus". Journal for the History of Astronomy. 18: 35–43. doi:10.1177/002182868701800102. S2CID 115311028.
  10. 1 2 Roberts, Victor (1957). "The Solar and Lunar Theory of Ibn ash-Shāṭir: A Pre-Copernican Copernican Model". Isis. 48 (4): 428–432. doi:10.1086/348609. ISSN 0021-1753. JSTOR 227515. S2CID 120033970.
  11. ↑ Roberts, Victor. "The Solar and Lunar Theory of Ibn ash-Shāṭir: A Pre-Copernican Copernican Model" (PDF). Chicago Journals. 48: 428–432 – via JSTOR.
  12. 1 2 Abbud, Fuad (1962). "The Planetary Theory of Ibn al-Shatir: Reduction of the Geometric Models to Numerical Tables". The University of Chicago Press. 53: 492–499 – via JSTOR.
  13. 1 2 3 Berggren, J (1999). "Sundials in medieval Islamic science and civilization" (PDF). Coordinates.
  14. ↑ Swerdlow, Noel M. (1973-12-31). "The Derivation and First Draft of Copernicus's Planetary Theory: A Translation of the Commentariolus with Commentary". Proceedings of the American Philosophical Society. 117 (6): 424. ISSN 0003-049X. JSTOR 986461.
  15. 1 2 King, David A. (2007). "Ibn al-Shāṭir: ʿAlāʾ al-Dīn ʿAlī ibn Ibrāhīm". In Thomas Hockey; et al. (eds.). The Biographical Encyclopedia of Astronomers. New York: Springer. pp. 569–70. ISBN 978-0-387-31022-0. (PDF version)
  16. ↑ Linton (2004, pp.124,137–38), Saliba (2009, pp.160–65).
  17. ↑ Roberts, Victor (1966). "The Planetary Theory of Ibn al-Shatir: Latitudes of the Planets". The University of Chicago. 57: 208–219 – via JSTOR.
  18. 1 2 "History of the sundial". National Maritime Museum. Archived from the original on 2007-10-10. Retrieved 2008-07-02.
  19. ↑ Jones 2005.
  20. ↑ (King 1983, pp. 547–8)
  21. 1 2 3 4 Rezvani, Pouyan. "The Role of ʿIlm al-Mīqāt in the Progress of Making Sundials in the Islamic Civilization" (PDF). Academia. Archived from the original (PDF) on 2021-12-19. Retrieved 2021-12-19.
  22. 1 2 King, David A. (1983). "The Astronomy of the Mamluks". Isis. 74 (4): 531–555 [545–546]. doi:10.1086/353360. S2CID 144315162.

References

  • Fernini, Ilias. A Bibliography of Scholars in Medieval Islam. Abu Dhabi (UAE) Cultural Foundation, 1998
  • Jones, Lawrence (December 2005). "The Sundial And Geometry". North American Sundial Society. 12 (4).
  • Kennedy, Edward S. (1966) "Late Medieval Planetary Theory." Isis 57:365–378.
  • Kennedy, Edward S. and Ghanem, Imad. (1976) The Life and Work of Ibn al-Shatir, an Arab Astronomer of the Fourteenth Century, History of Arabic Science Institute, University of Aleppo.
  • Linton, Chris. From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press, Cambridge, 2004, ISBN 978-0-521-82750-8.
  • Roberts, Victor. "The Solar and Lunar Theory of Ibn ash-Shatir: A Pre-Copernican Copernican Model". Isis, 48(1957):428–432.
  • Roberts, Victor and Edward S. Kennedy. "The Planetary Theory of Ibn al-Shatir". Isis, 50(1959):227–235.
  • Saliba, George. "Theory and Observation in Islamic Astronomy: The Work of Ibn al-Shatir of Damascus". Journal for the History of Astronomy, 18(1987):35–43.
  • Turner, Howard R. Science in Medieval Islam, an illustrated introduction. University of Texas Press, Austin, 1995. ISBN 0-292-78149-0 (pb) ISBN 0-292-78147-4 (hc)
  • Saliba, George (1994b), A History of Arabic Astronomy: Planetary Theories During the Golden Age of Islam, New York University Press, ISBN 978-0-8147-8023-7
  • Saliba, George (2009), "Islamic reception of Greek astronomy" (PDF), in Valls-Gabaud & Boskenberg (2009), vol. 260, pp. 149–65, Bibcode:2011IAUS..260..149S, doi:10.1017/S1743921311002237

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.