RLC – skrótowe oznaczenie dla obwodów elektrycznych (w tym elektronicznych) składających się tylko z trzech podstawowych elementów pasywnych:

• rezystora, oznaczanego przez R (rezystancja),
• cewki, oznaczanej przez L (indukcyjność),
• kondensatorów, oznaczanych przez C (pojemność).

Obwód RLC w układach prądu przemiennego

Drgania własne układu RLC

Schemat zamkniętego układu RLC.

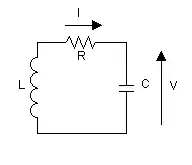
W szeregowym obwodzie RLC, w którym w chwili początkowej kondensator jest naładowany, a natężenie prądu jest równe 0, w dowolnej chwili ${\displaystyle t}$ suma energii kondensatora, energii cewki oraz praca prądu w ciągu czasu ${\displaystyle t}$ zamieniona na ciepło w oporze ${\displaystyle R}$ (tzn. na ciepło Joule’a-Lenza) jest równa energii początkowej kondensatora i jest stała.

${\displaystyle {\frac {Q^{2}}{2C}}+{\frac {LI^{2}}{2}}+\int _{0}^{t}I^{2}R\ dt={\frac {Q_{m}^{2}}{2C}}=const.}$

gdzie:

${\displaystyle Q_{m}}$ jest początkowym ładunkiem kondensatora.

Po zróżniczkowaniu obydwu stron powyższego równania względem czasu ${\displaystyle t{:}}$

${\displaystyle 2{\dot {Q}}{\frac {Q}{2C}}+2I{\frac {L{\dot {I}}}{2}}+I^{2}R=0.}$

Z definicji natężenia prądu:

${\displaystyle I={\frac {dQ}{dt}}={\dot {Q}},}$

${\displaystyle {\dot {I}}={\frac {dI}{dt}}={\frac {d({\dot {Q}})}{dt}}={\ddot {Q}}}$

można wyrazić w postaci:

${\displaystyle I\left({\frac {Q}{C}}+L{\ddot {Q}}+{\dot {Q}}R\right)=0.}$

Aby to równanie było spełnione w dowolnej chwili ${\displaystyle t,}$ wyrażenie w nawiasie powinno być równe 0. Po podzieleniu stronami przez ${\displaystyle L}$ otrzymujemy:

${\displaystyle {\ddot {Q}}+{\frac {R}{L}}{\dot {Q}}+{\frac {1}{LC}}Q=0.}$

Współczynnik przy ${\displaystyle Q}$ jest kwadratem pulsacji drgań własnych swobodnych obwodu ${\displaystyle LC{:}}$

${\displaystyle {\frac {1}{LC}}={\omega _{0}}^{2}.}$

Współczynnik przy pierwszej pochodnej ${\displaystyle {\dot {Q}}}$ oznaczamy przez ${\displaystyle 2\beta {:}}$

${\displaystyle {\frac {R}{L}}=2\beta \Rightarrow {\frac {R}{2L}}=\beta .}$

Równanie różniczkowe drgań elektrycznych gasnących:

${\displaystyle {\ddot {Q}}+2\beta {\dot {Q}}+{\omega _{0}}^{2}Q=0.}$

Rozwiązaniem tego równania jest wzór:

${\displaystyle Q=Q_{m}\ e^{-\beta t}\cos(\omega t+\varphi ).}$

Częstość drgań gasnących:

${\displaystyle \omega ={\sqrt {\omega _{0}^{2}-\beta ^{2}}}={\sqrt {{\frac {1}{LC}}-{\frac {R^{2}}{4L^{2}}}}},}$

${\displaystyle \beta ^{2}<\omega _{0}^{2}\Rightarrow {\frac {R^{2}}{4L^{2}}}<{\frac {1}{LC}},}$

co oznacza, iż rozwiązanie równania różniczkowego drgań elektrycznych gasnących ma miejsce przy niezbyt dużym tłumieniu.

Zmiana napięcia na kondensatorze:

${\displaystyle U={\frac {Q_{m}}{C}}\ e^{-\beta t}\cos(\omega t+\varphi )=U_{m}e^{-\beta t}\cos(\omega t+\varphi ).}$

Natężenie prądu jest przesunięte w fazie w stosunku do ładunku i napięcia na kondensatorze:

${\displaystyle I={\dot {Q}}=Q_{m}\ \omega _{0}\ e^{-\beta t}\left[-{\frac {\beta }{\omega _{0}}}\cos(\omega t+\varphi )-{\frac {\omega }{\omega _{0}}}\sin(\omega t+\varphi )\right]=Q_{m}\ \omega _{0}\ e^{-\beta t}\cos(\omega t+\varphi +\alpha ).}$

Dodatkowo:

${\displaystyle {\frac {\omega }{\omega _{0}}}=\sin \alpha }$ oraz ${\displaystyle {\frac {\beta }{\omega _{0}}}=-\cos \alpha .}$

Natężenie prądu zmienia się harmonicznie z amplitudą gasnącą wykładniczo, przy czym tangens przesunięcia fazowego natężenia prądu do napięcia wynosi:

${\displaystyle \operatorname {tg} \alpha =-{\frac {\omega }{\beta }}=-{\frac {\sqrt {\omega _{0}^{2}-\beta ^{2}}}{\beta }}=-{\frac {\sqrt {{\frac {1}{LC}}-{\frac {R^{2}}{4L^{2}}}}}{\frac {R}{2L}}}.}$

Dobroć obwodu, czyli wielkość proporcjonalna do liczby drgań N_e wykonywanych przez obwód w czasie, którego amplituda maleje ${\displaystyle e}$ razy

${\displaystyle D={\frac {\pi }{\delta }}={\frac {\pi }{\beta T}}={\frac {\omega }{2\beta }}.}$

Przy małym tłumieniu:

${\displaystyle \omega \approx \omega _{0}={\frac {1}{\sqrt {LC}}}.}$

Wobec czego:

${\displaystyle D\approx {\frac {\omega _{0}}{2\beta }}={\frac {1}{R}}{\sqrt {\frac {L}{C}}}.}$

Przykłady urządzeń zawierających obwód RLC

• filtr (elektronika)
• klasyczny układ zapłonowy z przerywaczem
• odbiornik radiowy
• telewizor
• transformator Tesli
• wykrywacz metalu
• zwrotnica głośnikowa

Linki zewnętrzne

• animacja szeregowego obwodu RLC (ang.)