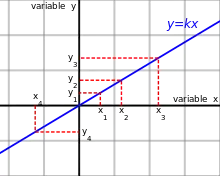
Zmienne proporcjonalne.

Proporcjonalność prosta – zależność między dwiema zmiennymi wielkościami x i y, w której iloraz tych wielkości jest stały (y/x = const)^[1]. Prowadzi to do wzoru

${\displaystyle y=ax,}$ gdzie a jest liczbą rzeczywistą różną od 0,

pozwalającego wyliczyć jedną z nich w zależności od drugiej. Obie wielkości są wprost proporcjonalne.

Przykłady

• W ruchu ze stałą prędkością przebyta droga jest wprost proporcjonalna do czasu jazdy.
• Wartość towaru zakupionego na wagę (przy danej cenie za jednostkę masy) jest wprost proporcjonalna do jego masy. Np. przy cenie jabłek 2 zł/kg (a=2), kupując 1 kg (x=1) zapłacimy 2 zł (y=2), kupując 2 kg (x=2) zapłacimy 4 zł (y=4), kupując 3 kg (x=3) zapłacimy 6 zł (y=6) itd.
• W spadku swobodnym (bez oporu powietrza) prędkość spadającego ciała jest wprost proporcjonalna do czasu spadania.
• Przy ustalonej stawce podatku jego wartość jest wprost proporcjonalna do kwoty, która podlega opodatkowaniu.

Zobacz też

• proporcja
• proporcjonalność odwrotna

Przypisy