Płatek Kocha

Krzywa Kocha – krzywa fraktalna, którą można zdefiniować jako pewien atraktor IFS lub jako granicę ciągu krzywych opisanych poniżej. Krzywa ta jest nieskończenie długa, mieści się jednak na skończonej powierzchni – można więc narysować pewne jej przybliżenie

Została ona opisana po raz pierwszy w pracy Sur une courbe continue sans tangente obtenue par une construction géométrique élémentaire przez Helgego von Kocha w roku 1904^[1].

Połączenie trzech krzywych przypomina płatek śniegu i nazywane jest płatkiem Kocha (na rysunku obok).

Krok 0

Krok 1

Krok 2

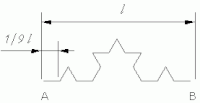
Tworzenie krzywej Kocha

Krzywa Kocha powstaje z odcinka, poprzez podzielenie go na 3 części i zastąpienie środkowej ząbkiem (o ramieniu długości równej 1/3 odcinka) takim, że wraz z usuwaną częścią tworzy trójkąt równoboczny. Krok ten jest powtarzany w nieskończoność, dla każdego fragmentu odcinka.

Krok 2

Krzywa Kocha w kroku drugim ${\displaystyle (k=2)}$ zawiera już 16 odcinków, każdy długości ${\displaystyle {\tfrac {1}{9}}l.}$ W kolejnym kroku ${\displaystyle (k=3)}$ powstanie 64 odcinków, każdy długości ${\displaystyle {\tfrac {1}{27}}l}$ itd.

7 pierwszych kroków algorytmu generującego krzywą Kocha.

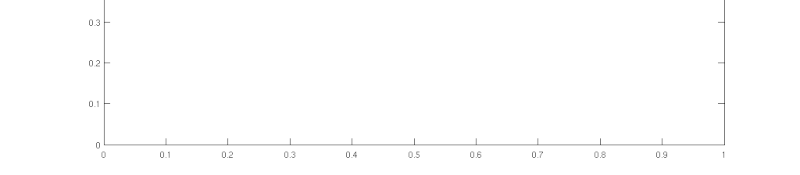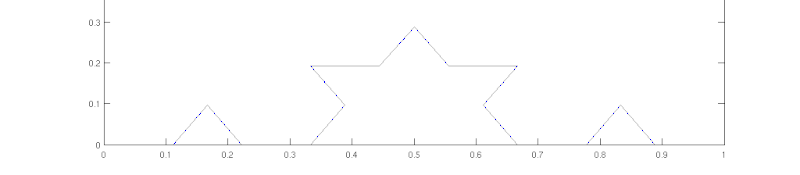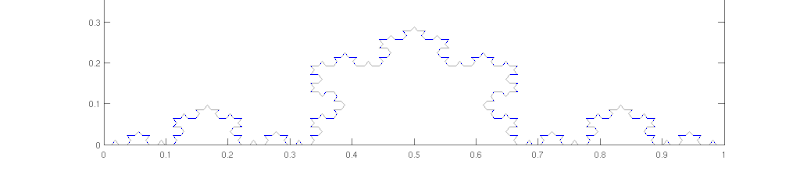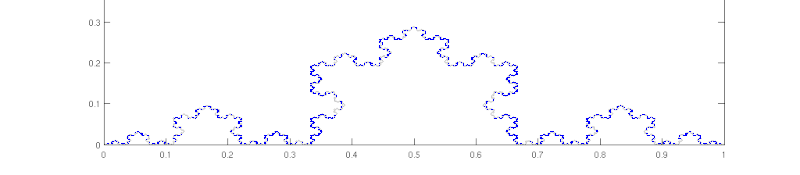
Wymiar

Aby obliczyć wymiar pojemnościowy (Kołmogorowa) krzywej Kocha, należy rozpatrzyć ${\displaystyle k}$-ty krok konstrukcji. Wtedy istnieje ${\displaystyle 4^{k}}$ odcinków, każdy długości ${\displaystyle ({\tfrac {1}{3}})^{k}=3^{-k},}$ tak więc:

${\displaystyle d=\lim \limits _{k\to \infty }{\frac {\log \left(4^{k}\right)}{\log \left({\frac {1}{3^{-k}}}\right)}}={\frac {\log(4)}{\log(3)}}\approx 1{,}26186}$

Zobacz też

• lista krzywych

Przypisy

Bibliografia

• Jacek Kudrewicz, Fraktale i chaos, WNT, Warszawa 2004.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Koch Snowflake, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).
• Płatek śniegu – konstrukcja i opis