Binegacja

Bramka NOR – jeden z funktorów zdaniowych rachunku zdań; dwuargumentowa funkcja boolowska (funktor logiczny) realizująca zaprzeczoną sumę logiczną (NOT OR) – jest prawdziwa wtedy i tylko wtedy, gdy oba składniki są fałszywe^[1]. Odpowiada wyrażeniu „ani … ani…”. Jego znaczenie przedstawia poniższa tablica prawdy:

Symbol bramki logicznej NOR

A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

Sposoby zapisu bramki NOR

$A\downarrow B$ – spójnik Sheffera^[2], przedstawiana za pomocą symbolu ↓ (pionowa kreska „|” przechodząca przez symbol alternatywy „ $\lor$ ” dwóch argumentów, co oznacza jej logiczną negację)
A NOR B
A ⊽ B – z użyciem symbolu ⊽ (U+22BD)
${\overline {A\lor B}}$ – gdzie symbol $\lor$ oznacza alternatywę (OR) natomiast kreska negację wyrażenia znajdującego się pod nią
$\neg (A\lor B)$ – jak wyżej z użyciem symbolu negacji ¬
${\overline {A+B}}$ – zanegowana suma logiczna

Wyrażanie funkcji boolowskiej w logice NOR

Jako że w bramki logiczne NAND i NOR są tańsze w produkcji niż AND i OR, a ponadto zapewniają stałość amplitudy sygnału wyjściowego, w faktycznych układach cyfrowych są one stosowane częściej niż „zwykłe” AND i OR.

Korzystając z praw de Morgana, możemy każdą funkcję boolowską przekształcić tak, aby korzystała tylko z bramek NOR.

Negacja (NOT)

Funkcja logiczna NOT przedstawiona za pomocą bramki NOR

Korzystając z jednego z aksjomatów algebry Boole’a:

a+a=a

Zapisać możemy równoważnie, że

Q={\overline {A+A}}={\overline {A}}

Co jest negacją zmiennej wejściowej.

Koniunkcja (AND)

Funkcja logiczna AND przedstawiona za pomocą bramek NOR

Skorzystamy tutaj z drugiego prawa de Morgana, które w ujęciu algebry Boole’a przyjmuje postać:

{\overline {a+b}}={\overline {a}}\cdot {\overline {b}}

Tak więc podając na wejście bramki NOR zanegowane zmienne wejściowe otrzymujemy koniunkcję tych zmiennych, co wyraża poniższe równanie:

Q={\overline {{\overline {A}}+{\overline {B}}}}={\overline {\overline {A}}}\cdot {\overline {\overline {B}}}=A\cdot B

Alternatywa (OR)

Funkcja logiczna OR przedstawiona za pomocą bramek NOR

W przypadku alternatywy jedynym wyjściem jest zanegowanie wyjścia bramki NOR, jako że podwójna negacja zmiennej daje tę samą zmienną.

Q={\overline {\overline {A+B}}}=A+B

Alternatywa wykluczająca (XOR)

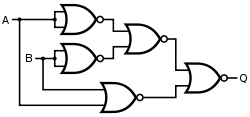
Funkcja logiczna XOR przedstawiona za pomocą bramek NOR

Układ realizujący funkcję XOR z bramek NOR budujemy w oparciu o wyjściowe równanie funkcji XOR wykorzystując przekształcenia pokazane wyżej.

Q=A\oplus B={\overline {A}}\cdot B+A\cdot {\overline {B}}=(A+B)\cdot ({\overline {A}}+{\overline {B}})={\overline {{\overline {A+B}}+{\overline {{\overline {A}}+{\overline {B}}}}}}

Zobacz też

Przypisy

↑ binegacja, [w:] Encyklopedia PWN [dostęp 2022-03-14] .
↑ Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), s. 37, ISBN 83-02-02551-8 .

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[epwn-1] binegacja, [w:] Encyklopedia PWN [dostęp 2022-03-14] .

[ES-2] Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), s. 37, ISBN 83-02-02551-8 .

[1]

[2]