Symbol ∴ (łac. „ergo”^[1][2]) stosowany jest w logice matematycznej i w dowodach matematycznych^[3]. Zazwyczaj używa się go przy wnioskowaniu, bezpośrednio przed konkluzją, na przykład przy wniosku sylogizmu^[4]. Czytany jest jako „stąd”^[5][6], „zatem”^[5] lub „w związku z tym”^[7] (ang. „therefore”^[6][8][9] lub ang. „consequently”^[9]). Symbol ten jest rzadko spotykany w Europie kontynentalnej^[10], jednak jest powszechnie używany w krajach anglosaskich^[11] i anglojęzycznej literaturze naukowej. Kodem tego symbolu w Unicode jest U+2234^[12].

Historia

Teutsche Algebra – pierwsze w historii udokumentowane użycie symbolu ∴ w kontekście wniosku logicznego

Pierwszy raz symbol ten pojawił się w druku w 1659 roku, w książce Teutsche Algebra (pol. „Niemiecka algebra”^[2]), której autorem jest Johann Rahn^[3]. W swojej pracy Rahn starał się przełożyć algebraiczny dorobek Viète’a i Kartezjusza na język niemiecki. W tym celu stosował liczne skróty notacyjne. Zdefiniował ∴ jako symbol mający nieść znaczenie łacińskiego ergo, czyli „zatem”^[1][2]. Zamiennie do niego używał również ∵, jednak później większość matematyków w tym znaczeniu używała wyłącznie pierwszego ze znaków^[10].

Przykłady użycia

Użycie w:

• sylogizmie^[13]:

• logice matematycznej^[8][14]:

${\displaystyle p\to q}$

${\displaystyle p}$

∴ ${\displaystyle q}$

• matematyce^[15]:

${\displaystyle x+y=z}$

∴ ${\displaystyle z-x=y}$

Inne zastosowania

W tradycji masońskiej symbol ∴ stosuje się jako znak abrewiatury. Stawiany po wielkich literach, bez spacji, sygnalizuje, że litery te stanowią skrót i są inicjałami tytułu masońskiego lub określenia stosowanego w wolnomularstwie^[16][17].

Alfabet Braille’a

Symbol ∴ występuje w standardzie Braille’a dla języka angielskiego (ang. „Unified English Braille”) w dwóch wersjach:

1. ^[18]
2. ^[19]

Podobnie wyglądające symbole

• ∵ (U+2235) również używany jest w logice matematycznej i czytany jest jako ponieważ lub od (ang. „because”)^[7][10];
• używany jest w meteorologii i oznacza „umiarkowany deszcz”^[20][21][22];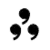
• używany jest w meteorologii i oznacza „umiarkowana mżawka”^[21][22];
• ⁂ (U+2042) używany jest w meteorologii i oznacza „umiarkowany śnieg”^[21][22];
• ஃ (U+0B83) w piśmie tamilskim jest znakiem spółgłoskowym o transliteracji ḵ^[23][24];
• ⛬ (U+26EC) jest japońskim symbolem mapowym oznaczającym miejsce historyczne^[25][26].

Przypisy

Bibliografia

• StefanS. Hugtenburg StefanS., Delftse Foundations of Computation, 2nd Edition, Minneapolis, MN 2018, ISBN 978-94-6366-598-8, OCLC 1345677665 [dostęp 2023-03-04]  (ang.).brak strony (książka)
• Johann HeinrichJ.H. Rahn Johann HeinrichJ.H., Teutsche Algebra, 1659, OCLC 166125548 [dostęp 2023-03-12] [zarchiwizowane z adresu 2023-03-12]  (niem.).brak strony (książka)