In geometry, the Yff center of congruence is a special point associated with a triangle. This special point is a triangle center and Peter Yff initiated the study of this triangle center in 1987.^[1]

Isoscelizer

An isoscelizer of an angle A in a triangle △ABC is a line through points P₁, Q₁, where P₁ lies on AB and Q₁ on AC, such that the triangle △AP₁Q₁ is an isosceles triangle. An isoscelizer of angle A is a line perpendicular to the bisector of angle A. Isoscelizers were invented by Peter Yff in 1963.^[2]

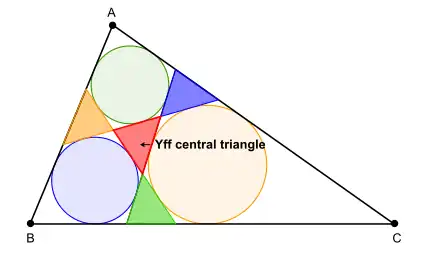
Yff central triangle

  Reference triangle △ABC

  △A'P₂Q₃ ≅   △Q₁B'P₃ ≅   △P₁Q₂C' ≅

  △A'B'C' (Yff central triangle)

Let △ABC be any triangle. Let P₁Q₁ be an isoscelizer of angle A, P₂Q₂ be an isoscelizer of angle B, and P₃Q₃ be an isoscelizer of angle C. Let △A'B'C' be the triangle formed by the three isoscelizers. The four triangles △A'P₂Q₃, △Q₁B'P₃, △P₁Q₂C', and △A'B'C' are always similar.

There is a unique set of three isoscelizers P₁Q₁, P₂Q₂, P₃Q₃ such that the four triangles △A'P₂Q₃, △Q₁B'P₃, △P₁Q₂C', and △A'B'C' are congruent. In this special case △A'B'C' formed by the three isoscelizers is called the Yff central triangle of △ABC.^[3]

The circumcircle of the Yff central triangle is called the Yff central circle of the triangle.

Yff center of congruence

Animation showing the continuous shrinking of the Yff central triangle to the Yff center of congruence. The animation also shows the continuous expansion of the Yff central triangle until the three outer triangles reduce to points on the sides of the triangle.

Let △ABC be any triangle. Let P₁Q₁, P₂Q₂, P₃Q₃ be the isoscelizers of the angles A, B, C such that the triangle △A'B'C' formed by them is the Yff central triangle of △ABC. The three isoscelizers P₁Q₁, P₂Q₂, P₃Q₃ are continuously parallel-shifted such that the three triangles △A'P₂Q₃, △Q₁B'P₃, △P₁Q₂C' are always congruent to each other until △A'B'C' formed by the intersections of the isoscelizers reduces to a point. The point to which △A'B'C' reduces to is called the Yff center of congruence of △ABC.

Properties

Any triangle △ABC is the triangle formed by the lines which are externally tangent to the three excircles of the Yff central triangle of △ABC.

• The trilinear coordinates of the Yff center of congruence are^[1]
  $${\displaystyle \sec {\frac {A}{2}}:\sec {\frac {B}{2}}:\sec {\frac {C}{2}}}$$

  
• Any triangle △ABC is the triangle formed by the lines which are externally tangent to the three excircles of the Yff central triangle of △ABC.
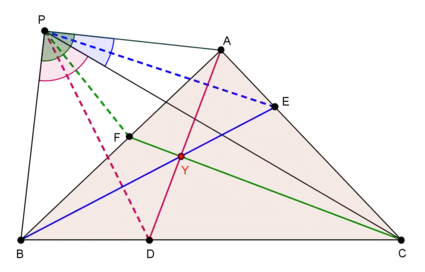
• Let I be the incenter of △ABC. Let D be the point on side BC such that ∠BID = ∠DIC, E a point on side CA such that ∠CIE = ∠EIA, and F a point on side AB such that ∠AIF = ∠FIB. Then the lines AD, BE, CF are concurrent at the Yff center of congruence. This fact gives a geometrical construction for locating the Yff center of congruence.^[4]
• A computer assisted search of the properties of the Yff central triangle has generated several interesting results relating to properties of the Yff central triangle.^[5]

Generalization of Yff centre of congruence

Generalization

The geometrical construction for locating the Yff center of congruence has an interesting generalization. The generalisation begins with an arbitrary point P in the plane of a triangle △ABC. Then points D, E, F are taken on the sides BC, CA, AB such that

$${\displaystyle \angle BPD=\angle DPC,\quad \angle CPE=\angle EPA,\quad \angle APF=\angle FPB.}$$

The generalization asserts that the lines AD, BE, CF are concurrent.^[4]

See also

• Congruent isoscelizers point
• Central triangle

References