| Set of uniform antiprismatic prisms | |
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | s{2,p}×{} |
| Coxeter diagram | |
| Cells | 2 p-gonal antiprisms, 2 p-gonal prisms and 2p triangular prisms |
| Faces | 4p {3}, 4p {4} and 4 {p} |
| Edges | 10p |
| Vertices | 4p |
| Vertex figure |  Trapezoidal pyramid |
| Symmetry group | [2p,2+,2], order 8p [(p,2)+,2], order 4p |
| Properties | convex if the base is convex |
In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a p-gonal antiprismatic prism is [2p,2+,2], order 8p.
A p-gonal antiprismatic prism or p-gonal antiduoprism has 2 p-gonal antiprism, 2 p-gonal prism, and 2p triangular prism cells. It has 4p equilateral triangle, 4p square and 4 regular p-gon faces. It has 10p edges, and 4p vertices.
 Schlegel diagram |
 Net |
Convex uniform antiprismatic prisms
There is an infinite series of convex uniform antiprismatic prisms, starting with the digonal antiprismatic prism is a tetrahedral prism, with two of the tetrahedral cells degenerated into squares. The triangular antiprismatic prism is the first nondegenerate form, which is also an octahedral prism. The remainder are unique uniform 4-polytopes.
| Name | s{2,2}×{} | s{2,3}×{} | s{2,4}×{} | s{2,5}×{} | s{2,6}×{} | s{2,7}×{} | s{2,8}×{} | s{2,p}×{} |
|---|---|---|---|---|---|---|---|---|
| Coxeter diagram |
||||||||
| Image |  |
 |
 |
 |
 |
 |
 |
 |
| Vertex figure |
 |
 |
||||||
| Cells | 2 s{2,2} (2) {2}×{}={4} 4 {3}×{} |
2 s{2,3} 2 {3}×{} 6 {3}×{} |
2 s{2,4} 2 {4}×{} 8 {3}×{} |
2 s{2,5} 2 {5}×{} 10 {3}×{} |
2 s{2,6} 2 {6}×{} 12 {3}×{} |
2 s{2,7} 2 {7}×{} 14 {3}×{} |
2 s{2,8} 2 {8}×{} 16 {3}×{} |
2 s{2,p} 2 {p}×{} 2p {3}×{} |
| Net |  |
 |
 |
 |
 |
 |
 |
 |
Star antiprismatic prisms
There are also star forms following the set of star antiprisms, starting with the pentagram {5/2}:
| Name | Coxeter diagram |
Cells | Image | Net |
|---|---|---|---|---|
| Pentagrammic antiprismatic prism 5/2 antiduoprism |
2 pentagrammic antiprisms 2 pentagrammic prisms 10 triangular prisms |  |  | |
| Pentagrammic crossed antiprismatic prism 5/3 antiduoprism |
2 pentagrammic crossed antiprisms 2 pentagrammic prisms 10 triangular prisms |  |  | |
| ... |
Square antiprismatic prism
| Square antiprismatic prism | |
|---|---|
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | s{2,4}x{} |
| Coxeter-Dynkin | |
| Cells | 2 (3.3.3.4) 8 (3.4.4) 2 4.4.4 |
| Faces | 16 {3}, 20 {4} |
| Edges | 40 |
| Vertices | 16 |
| Vertex figure | Trapezoidal pyramid |
| Symmetry group | [(4,2)+,2], order 16 [8,2+,2], order 32 |
| Properties | convex |
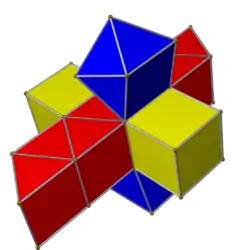
A square antiprismatic prism or square antiduoprism is a convex uniform 4-polytope. It is formed as two parallel square antiprisms connected by cubes and triangular prisms. The symmetry of a square antiprismatic prism is [8,2+,2], order 32. It has 16 triangle, 16 square and 4 square faces. It has 40 edges, and 16 vertices.
 Schlegel diagram |
 Net |
Pentagonal antiprismatic prism
| Pentagonal antiprismatic prism | |
|---|---|
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | s{2,5}x{} |
| Coxeter-Dynkin | |
| Cells | 2 (3.3.3.5) 10 (3.4.4) 2 (4.4.5) |
| Faces | 20 {3}, 20 {4}, 4 {5} |
| Edges | 50 |
| Vertices | 20 |
| Vertex figure | Trapezoidal pyramid |
| Symmetry group | [(5,2)+,2], order 20 [10,2+,2], order 40 |
| Properties | convex |
A pentagonal antiprismatic prism or pentagonal antiduoprism is a convex uniform 4-polytope. It is formed as two parallel pentagonal antiprisms connected by cubes and triangular prisms. The symmetry of a pentagonal antiprismatic prism is [10,2+,2], order 40. It has 20 triangle, 20 square and 4 pentagonal faces. It has 50 edges, and 20 vertices.
 Schlegel diagram |
 Net |
Hexagonal antiprismatic prism
| Hexagonal antiprismatic prism | |
|---|---|
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | s{2,6}x{} |
| Coxeter-Dynkin | |
| Cells | 2 (3.3.3.6) 12 (3.4.4) 2 (4.4.6) |
| Faces | 24 {3}, 24 {4}, 4 {6} |
| Edges | 60 |
| Vertices | 24 |
| Vertex figure | Trapezoidal pyramid |
| Symmetry group | [(2,6)+,2], order 24 [12,2+,2], order 48 |
| Properties | convex |
A hexagonal antiprismatic prism or hexagonal antiduoprism is a convex uniform 4-polytope. It is formed as two parallel hexagonal antiprisms connected by cubes and triangular prisms. The symmetry of a hexagonal antiprismatic prism is [12,2+,2], order 48. It has 24 triangle, 24 square and 4 hexagon faces. It has 60 edges, and 24 vertices.
 Schlegel diagram |
 Net |
Heptagonal antiprismatic prism
| Heptagonal antiprismatic prism | |
|---|---|
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | s{2,7}×{} |
| Coxeter-Dynkin | |
| Cells | 2 (3.3.3.7) 14 (3.4.4) 2 (4.4.7) |
| Faces | 28 {3}, 28 {4}, 4 {7} |
| Edges | 70 |
| Vertices | 28 |
| Vertex figure | Trapezoidal pyramid |
| Symmetry group | [(7,2)+,2], order 28 [14,2+,2], order 56 |
| Properties | convex |
A heptagonal antiprismatic prism or heptagonal antiduoprism is a convex uniform 4-polytope. It is formed as two parallel heptagonal antiprisms connected by cubes and triangular prisms. The symmetry of a heptagonal antiprismatic prism is [14,2+,2], order 56. It has 28 triangle, 28 square and 4 heptagonal faces. It has 70 edges, and 28 vertices.
 Schlegel diagram |
 Net |
Octagonal antiprismatic prism
| Octagonal antiprismatic prism | |
|---|---|
| Type | Prismatic uniform 4-polytope |
| Schläfli symbol | s{2,8}×{} |
| Coxeter-Dynkin | |
| Cells | 2 (3.3.3.8) 16 (3.4.4) 2 (4.4.8) |
| Faces | 32 {3}, 32 {4}, 4 {8} |
| Edges | 80 |
| Vertices | 32 |
| Vertex figure | Trapezoidal pyramid |
| Symmetry group | [(8,2)+,2], order 32 [16,2+,2], order 64 |
| Properties | convex |
A octagonal antiprismatic prism or octagonal antiduoprism is a convex uniform 4-polytope (four-dimensional polytope). It is formed as two parallel octagonal antiprisms connected by cubes and triangular prisms. The symmetry of an octagonal antiprismatic prism is [16,2+,2], order 64. It has 32 triangle, 32 square and 4 octagonal faces. It has 80 edges, and 32 vertices.
 Schlegel diagram |
 Net |
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
External links
- 6. Convex uniform prismatic polychora, George Olshevsky.