Sinusoidal spirals (rⁿ = –1ⁿ cos(nθ), θ = π/2) in polar coordinates and their equivalents in rectangular coordinates:

  n = −2: Equilateral hyperbola

  n = −1: Line

  n = −1/2: Parabola

  n = 1/2: Cardioid

  n = 1: Circle

  n = 2: Lemniscate of Bernoulli

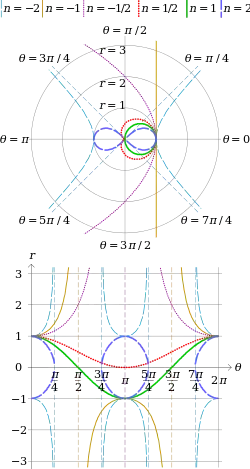
In algebraic geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

where a is a nonzero constant and n is a rational number other than 0. With a rotation about the origin, this can also be written

${\displaystyle r^{n}=a^{n}\sin(n\theta ).\,}$

The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including:

• Rectangular hyperbola (n = −2)
• Line (n = −1)
• Parabola (n = −1/2)
• Tschirnhausen cubic (n = −1/3)
• Cayley's sextet (n = 1/3)
• Cardioid (n = 1/2)
• Circle (n = 1)
• Lemniscate of Bernoulli (n = 2)

The curves were first studied by Colin Maclaurin.

Equations

Differentiating

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

and eliminating a produces a differential equation for r and θ:

${\displaystyle {\frac {dr}{d\theta }}\cos n\theta +r\sin n\theta =0}$.

Then

${\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)\cos n\theta {\frac {ds}{d\theta }}=\left(-r\sin n\theta ,\ r\cos n\theta \right)=r\left(-\sin n\theta ,\ \cos n\theta \right)}$

which implies that the polar tangential angle is

${\displaystyle \psi =n\theta \pm \pi /2}$

and so the tangential angle is

${\displaystyle \varphi =(n+1)\theta \pm \pi /2}$.

(The sign here is positive if r and cos nθ have the same sign and negative otherwise.)

The unit tangent vector,

${\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)}$,

has length one, so comparing the magnitude of the vectors on each side of the above equation gives

${\displaystyle {\frac {ds}{d\theta }}=r\cos ^{-1}n\theta =a\cos ^{-1+{\tfrac {1}{n}}}n\theta }$.

In particular, the length of a single loop when ${\displaystyle n>0}$ is:

${\displaystyle a\int _{-{\tfrac {\pi }{2n}}}^{\tfrac {\pi }{2n}}\cos ^{-1+{\tfrac {1}{n}}}n\theta \ d\theta }$

The curvature is given by

${\displaystyle {\frac {d\varphi }{ds}}=(n+1){\frac {d\theta }{ds}}={\frac {n+1}{a}}\cos ^{1-{\tfrac {1}{n}}}n\theta }$.

Properties

The inverse of a sinusoidal spiral with respect to a circle with center at the origin is another sinusoidal spiral whose value of n is the negative of the original curve's value of n. For example, the inverse of the lemniscate of Bernoulli is a rectangular hyperbola.

The isoptic, pedal and negative pedal of a sinusoidal spiral are different sinusoidal spirals.

One path of a particle moving according to a central force proportional to a power of r is a sinusoidal spiral.

When n is an integer, and n points are arranged regularly on a circle of radius a, then the set of points so that the geometric mean of the distances from the point to the n points is a sinusoidal spiral. In this case the sinusoidal spiral is a polynomial lemniscate.

Wikimedia Commons has media related to Sinusoidal spiral.

References

• Yates, R. C.: A Handbook on Curves and Their Properties, J. W. Edwards (1952), "Spiral" p. 213–214
• "Sinusoidal spiral" at www.2dcurves.com
• "Sinusoidal Spirals" at The MacTutor History of Mathematics
• Weisstein, Eric W. "Sinusoidal Spiral". MathWorld.