In enzyme kinetics, a secondary plot uses the intercept or slope from several Lineweaver–Burk plots to find additional kinetic constants.^[1][2]

For example, when a set of v by [S] curves from an enzyme with a ping–pong mechanism (varying substrate A, fixed substrate B) are plotted in a Lineweaver–Burk plot, a set of parallel lines will be produced.

The following Michaelis–Menten equation relates the initial reaction rate v₀ to the substrate concentrations [A] and [B]:

${\displaystyle {\begin{aligned}{\frac {1}{v_{0}}}&={\frac {K_{M}^{A}}{v_{\max }{[}A{]}}}+{\frac {K_{M}^{B}}{v_{\max }{[}B{]}}}+{\frac {1}{v_{\max }}}\end{aligned}}}$

The y-intercept of this equation is equal to the following:

${\displaystyle {\begin{aligned}{\mbox{y-intercept}}={\frac {K_{M}^{B}}{v_{\max }{[}B{]}}}+{\frac {1}{v_{\max }}}\end{aligned}}}$

The y-intercept is determined at several different fixed concentrations of substrate B (and varying substrate A). The y-intercept values are then plotted versus 1/[B] to determine the Michaelis constant for substrate B, ${\displaystyle K_{M}^{B}}$, as shown in the Figure to the right.^[3] The slope is equal to ${\displaystyle K_{M}^{B}}$ divided by ${\displaystyle v_{\max }}$ and the intercept is equal to 1 over ${\displaystyle v_{\max }}$.

Secondary Plot of enzyme system Horseradish Peroxidase and o-Phenylenediamine (with hydrogen peroxide as the second substrate)

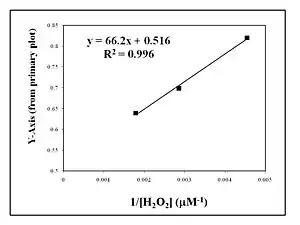
Secondary plot in inhibition studies

A secondary plot may also be used to find a specific inhibition constant, K_I.

For a competitive enzyme inhibitor, the apparent Michaelis constant is equal to the following:

${\displaystyle {\begin{aligned}{\mbox{apparent }}K_{m}=K_{m}\times \left(1+{\frac {[I]}{K_{I}}}\right)\end{aligned}}}$

The slope of the Lineweaver-Burk plot is therefore equal to:

${\displaystyle {\begin{aligned}{\mbox{slope}}={\frac {K_{m}}{v_{\max }}}\times \left(1+{\frac {[I]}{K_{I}}}\right)\end{aligned}}}$

If one creates a secondary plot consisting of the slope values from several Lineweaver-Burk plots of varying inhibitor concentration [I], the competitive inhbition constant may be found. The slope of the secondary plot divided by the intercept is equal to 1/K_I. This method allows one to find the K_I constant, even when the Michaelis constant and v_max values are not known.

References