| Computing devices in |
| Rabdology |
|---|
| Napier's bones |
| Promptuary |
| Location arithmetic |
The promptuary, also known as the card abacus is a calculating machine invented by the 16th-century Scottish mathematician John Napier and described in his book Rabdologiae[1] in which he also described Napier's bones.
It is an extension of Napier's Bones, using two sets of rods to achieve multi-digit multiplication without the need to write down intermediate results, although some mental addition is still needed to calculate the result. The rods for the multiplicand are similar to Napier's Bones, with repetitions of the values. The set of rods for the multiplier are shutters or masks for each digit placed over the multiplicand rods. The results are then tallied from the digits showing as with other lattice multiplication methods.
The final form described by Napier took advantage of symmetries to compact the rods, and used the materials of the day to hold system of metal plates, placed inside a wooden frame.[2]
Design of the Promptuary
The promptuary consists of four parts:
- a set of number strips, engraved with a large digit at one end and with many small digits along the strip
- a set of mask strips, which Napier called excised or perforated strips. Each has a single digit engraved at one end and various triangular holes cut in it
- a board on which to place the strips when performing a calculation
- a box to store the strips. In Napier's design, the top of the box was the board on which the calculations were performed.
The dimensions of the strips depends on the maximum number of digits in the numbers to be multiplied. For a device capable of multiplying two N-digit numbers together, the strips should be (N+1) times as long as they are wide, and there should be 10N number strips and 10N mask strips. So for example, for a promptuary capable of multiplying two five-digit numbers together, the strips should 6 times as long as they are wide, with 50 number strips and 50 mask strips. Napier's example specified strips 1 finger (19mm) wide and 11 fingers (209mm) long, enabling the device to multiply two 10-digits numbers to produce a 20-digit result.
Napier specified that the number strips should be a different thickness from the mask strips - one quarter of a finger (5mm) versus one eight of a finger (2.5mm). This is not necessary for the operation of the device.
The promptuary contains a lot more pieces than a set of Napier's Bones. A set of Napier's Bones with 20 rods is capable of multiplying numbers of up to 8 digits. An equivalent promptuary needs 160 strips.
In the examples and illustrations below, N is set to 5 - that is, the illustrated promptuary can multiply numbers of up to 5 digits.
Number Strips
The number strips are divided into five squares, with about half a square free at each end. A large digit, known as the simple, is marked in the space at the top of the strip. A multiplication table is placed in each of the five squares. Each of these multiplication tables is identical—it lists the multiples of the simple and is laid out in a particular way:
The square is divided into nine smaller squares in a three-by-three arrangement. Each of these is divided into two triangles by a diagonal line running from lower left to upper right. The multiples of the digit at the top of the strip, the simple, are marked in the table as in the diagram.
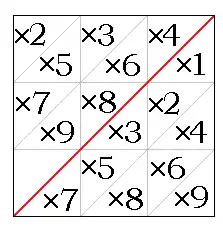
- The simple itself is marked in the triangle labelled × 1.
- The number that is two times the simple is marked in the two triangles marked × 2. If the number is two digits, the first digit is placed to the left of the main diagonal (marked in red) and the second digit to the right of the diagonal. If the number is a single digit, it is marked to the right of the diagonal
- The number that is 3 times the simple is written in the triangles marked × 3 in the same way as the multiple of 2
- The other multiplies of the simple are marked in the other triangles in the same way.
- Zeroes may be written in or left blank. This does not affect the operation of the device.
- The triangle in the bottom left of the table is always blank.
The following diagram shows the multiplication table for the simple 7:
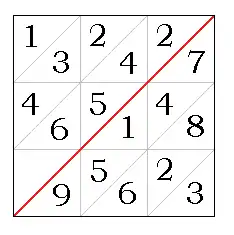
Complete number strips for the simple 7 and the simple 2 are shown in the following diagram. The lines delineating the triangles have been omitted.

The Mask Strips
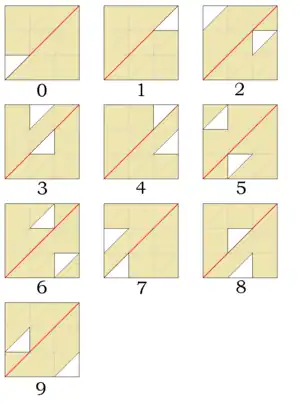
Mask strips are placed horizontally across the calculating board, that is, from left to right rather than from top to bottom. They have a large digit written in the space at one end and the rest of the strip contains five squares. Each square has triangular holes cut in it according to the patterns given in the following diagram.
So for example the mask strips for the simples 3, 6 and 9 will look as follows:
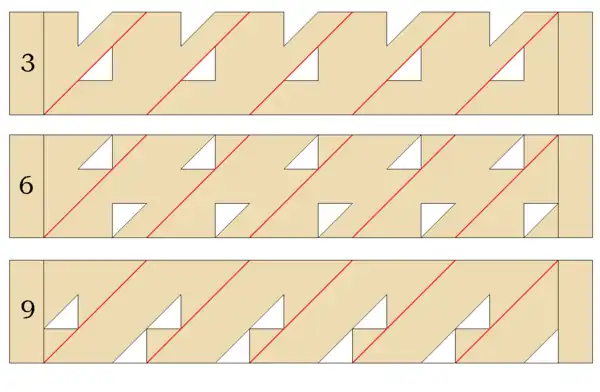
The guide lines in the patterns are for positioning the holes. They do not need to appear on the strips. The main diagonal line of each mask pattern, however, shown here in red, is marked on the mask strip. It is an important part of the device. The pattern given here for the simple 0 is from later editions of Napier's book. The version of the 0 strip in the first edition had no holes in it.
Performing a Multiplication
Number strips for the first of the numbers to be multiplied, the multiplicand, are placed on the calculating board side by side, running from top to bottom of the board. In the example shown here, the multiplicand is 772.
Mask strips for the second number, the multiplier, are placed horizontally on top of the number strips. In the example, the multiplier it 396.
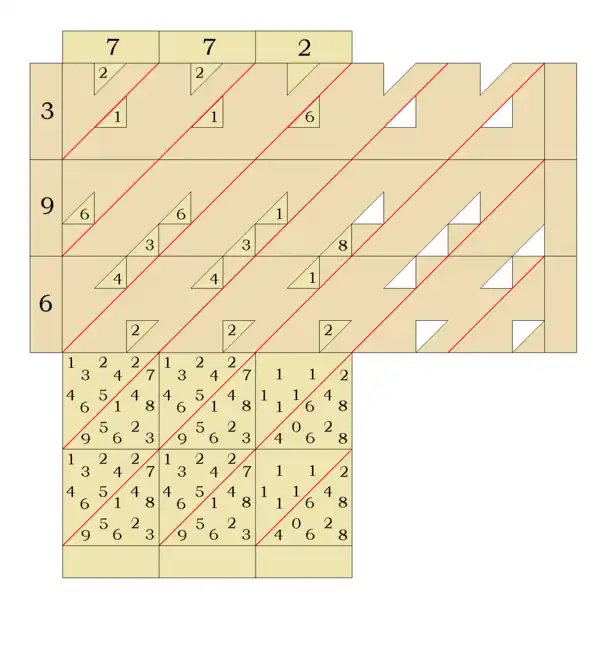
The result of the multiplication is read from the device by examining the digits visible through the triangular holes in the mask strips. Those parts of the number strips that are not covered by the mask strips are ignored. The diagonal lines on the mask strips divide the device into diagonal bands containing digits visible through the holes.
- Starting at the right, the first band with any visible digits contains just one digit, a 2. This is written down as the right-most digit of the result.
- The next band from the right has three digits, 2, 1 and 8. These are added together to get 11. The units digit of this addition, 1, is written down as the next digit of the multiplication result. The tens digit, which is 1, is carried into the next band.
- The third band from the right has five digits, 2, 4, 3, 1 and 6 plus the carried 1. These are all added to produce 17. The units digit of this, 7, is written as the next digit of the result. The tens digit, 1, is carried into the next band.
- This process is repeated for each diagonal band from right to left until all the digits have been processed.
The full result has now been written down as 305712. This is the result of multiplying 772 by 396. The multiplication process required only addition, and no intermediate results needed to be written down.
An Example of the Promptuary in the National Archaeological Museum of Spain
_01.jpg.webp)
An example of the Promptuary is in the National Archaeological Museum of Spain in Madrid. It also includes an example of Napier's bones.
The apparatus is a box of wood with inlays of bone. In the top section it contains the "bones" calculation device, and in the bottom section is the promptuary. This example consists of 300 stored cards in 30 drawers. One hundred of these cards are covered with numbers (referred to as the number cards). The remaining two hundred cards contain small triangular holes, which, when laid on top of the number cards, allow the user to see only certain numbers. By the capable positioning of these cards, multiplications can be made up to the limit of a number 10 digits in length, by another number 20 digits in length.
In addition, the doors of the box contain the first powers of the digits, the coefficients of the terms of the first powers of the binomial and the numeric data of the regular polyhedra.[3]
It is not known who was the maker of this piece, nor if it is of Spanish origin or came from a foreigner, although it is probable that it originally belonged to the Spanish Academy of Mathematics (which was created by Philip II) or was a gift from the Prince of Wales. The only thing that is sure is that it was conserved in the Palace, whence it was passed to the National library and later to the National Archaeological Museum, where it is still conserved.
In 1876, the Spanish government sent the apparatus to the exhibition of scientific instruments in Kensington, where it received so much attention that several societies consulted the Spanish representation about the origin and use of the apparatus.
References
- ↑ John Napier (1990) [1617]. Rabdologiæ [Rabdology] (in Latin). Translated by William Frank Richardson. Introduction by Robin E. Rider. MIT Press. ISBN 0-262-14046-2.
- ↑ Bradley, Michael John (2006), The Age of Genius: 1300 to 1800, Infobase Publishing, p. 36, ISBN 978-0-8160-5424-4.
- ↑ Diccionario enciclopédico hispano-americano de literatura, ciencias y artes, Mountainer y Simón Editores, Barcelona, 1887, Tomo I, pp. 19–20.