Planar tangle

A (shaded) planar tangle is the data of finitely many input disks, one output disk, non-intersecting strings giving an even number, say ${\displaystyle 2n}$, intervals per disk and one ${\displaystyle \star }$-marked interval per disk.

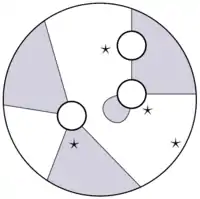
Here, the mark is shown as a ${\displaystyle \star }$-shape. On each input disk it is placed between two adjacent outgoing strings, and on the output disk it is placed between two adjacent incoming strings. A planar tangle is defined up to isotopy.

Composition

To compose two planar tangles, put the output disk of one into an input of the other, having as many intervals, same shading of marked intervals and such that the ${\displaystyle \star }$-marked intervals coincide. Finally we remove the coinciding circles. Note that two planar tangles can have zero, one or several possible compositions.

Planar operad

The planar operad is the set of all the planar tangles (up to isomorphism) with such compositions.

Planar algebra

A planar algebra is a representation of the planar operad; more precisely, it is a family of vector spaces ${\displaystyle ({\mathcal {P}}_{n,\pm })_{n\in \mathbb {N} }}$, called ${\displaystyle n}$-box spaces, on which acts the planar operad, i.e. for any tangle ${\displaystyle T}$ (with one output disk and ${\displaystyle r}$ input disks with ${\displaystyle 2n_{0}}$ and ${\displaystyle 2n_{1},\dots ,2n_{r}}$ intervals respectively) there is a multilinear map

${\displaystyle Z_{T}:{\mathcal {P}}_{n_{1},\epsilon _{1}}\otimes \cdots \otimes {\mathcal {P}}_{n_{r},\epsilon _{r}}\to {\mathcal {P}}_{n_{0},\epsilon _{0}}}$

with ${\displaystyle \epsilon _{i}\in \{+,-\}}$ according to the shading of the ${\displaystyle \star }$-marked intervals, and these maps (also called partition functions) respect the composition of tangle in such a way that all the diagrams as below commute.

Planar tangles

The family of vector spaces ${\displaystyle ({\mathcal {T}}_{n,\pm })_{n\in \mathbb {N} }}$ generated by the planar tangles having ${\displaystyle 2n}$ intervals on their output disk and a white (or black) ${\displaystyle \star }$-marked interval, admits a planar algebra structure.

Temperley–Lieb

The Temperley-Lieb planar algebra ${\displaystyle {\mathcal {TL}}(\delta )}$ is generated by the planar tangles without input disk; its ${\displaystyle 3}$-box space ${\displaystyle {\mathcal {TL}}_{3,+}(\delta )}$ is generated by

Moreover, a closed string is replaced by a multiplication by ${\displaystyle \delta }$.

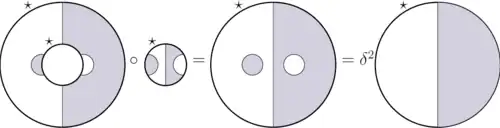
Note that the dimension of ${\displaystyle {\mathcal {TL}}_{n,\pm }(\delta )}$ is the Catalan number ${\displaystyle {\frac {1}{n+1}}{\binom {2n}{n}}}$. This planar algebra encodes the notion of Temperley–Lieb algebra.

Hopf algebra

A semisimple and cosemisimple Hopf algebra over an algebraically closed field is encoded in a planar algebra defined by generators and relations, and "corresponds" (up to isomorphism) to a connected, irreducible, spherical, non degenerate planar algebra with non zero modulus ${\displaystyle \delta }$ and of depth two.^[7]

Note that connected means ${\displaystyle \dim({\mathcal {P}}_{0,\pm })=1}$ (as for evaluable below), irreducible means ${\displaystyle \dim({\mathcal {P}}_{1,+})=1}$, spherical is defined below, and non-degenerate means that the traces (defined below) are non-degenerate.

Definition

A subfactor planar algebra is a planar ${\displaystyle \star }$-algebra ${\displaystyle ({\mathcal {P}}_{n,\pm })_{n\in \mathbb {N} }}$ which is:

(1) Finite-dimensional: ${\displaystyle \dim({\mathcal {P}}_{n,\pm })<\infty }$

(2) Evaluable: ${\displaystyle {\mathcal {P}}_{0,\pm }=\mathbb {C} }$

(3) Spherical: ${\displaystyle tr:=tr_{r}=tr_{l}}$

(4) Positive: ${\displaystyle \langle a\vert b\rangle =tr(b^{\star }a)}$ defines an inner product.

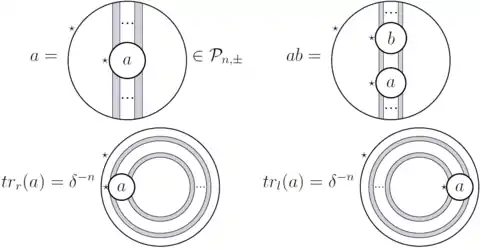
Note that by (2) and (3), any closed string (shaded or not) counts for the same constant ${\displaystyle \delta }$.

The tangle action deals with the adjoint by:

${\displaystyle Z_{T}(a_{1}\otimes a_{2}\otimes \cdots \otimes a_{r})^{\star }=Z_{T^{\star }}(a_{1}^{\star }\otimes a_{2}^{\star }\otimes \cdots \otimes a_{r}^{\star })}$

with ${\displaystyle T^{\star }}$ the mirror image of ${\displaystyle T}$ and ${\displaystyle a_{i}^{\star }}$ the adjoint of ${\displaystyle a_{i}}$ in ${\displaystyle {\mathcal {P}}_{n_{i},\epsilon _{i}}}$.

Examples and results

No-ghost theorem: The planar algebra ${\displaystyle {\mathcal {TL}}(\delta )}$ has no ghost (i.e. element ${\displaystyle a}$ with ${\displaystyle \langle a\vert a\rangle <0}$) if and only if

${\displaystyle \delta \in \{2\cos(\pi /n)|n=3,4,5,...\}\cup [2,+\infty ]}$

For ${\displaystyle \delta }$ as above, let ${\displaystyle {\mathcal {I}}}$ be the null ideal (generated by elements ${\displaystyle a}$ with ${\displaystyle \langle a\vert a\rangle =0}$). Then the quotient ${\displaystyle {\mathcal {TL}}(\delta )/{\mathcal {I}}}$ is a subfactor planar algebra, called the Temperley–Lieb-Jones subfactor planar algebra ${\displaystyle {\mathcal {TLJ}}(\delta )}$. Any subfactor planar algebra with constant ${\displaystyle \delta }$ admits ${\displaystyle {\mathcal {TLJ}}(\delta )}$ as planar subalgebra.

A planar algebra ${\displaystyle ({\mathcal {P}}_{n,\pm })}$ is a subfactor planar algebra if and only if it is the standard invariant of an extremal subfactor ${\displaystyle N\subseteq M}$ of index ${\displaystyle [M:N]=\delta ^{2}}$, with ${\displaystyle {\mathcal {P}}_{n,+}=N'\cap M_{n-1}}$ and ${\displaystyle {\mathcal {P}}_{n,-}=M'\cap M_{n}}$.^[8][9][10] A finite depth or irreducible subfactor is extremal (${\displaystyle tr_{N'}=tr_{M}}$ on ${\displaystyle N'\cap M}$).

There is a subfactor planar algebra encoding any finite group (and more generally, any finite dimensional Hopf ${\displaystyle {\rm {C}}^{\star }}$-algebra, called Kac algebra), defined by generators and relations. A (finite dimensional) Kac algebra "corresponds" (up to isomorphism) to an irreducible subfactor planar algebra of depth two.^[11][12]

The subfactor planar algebra associated to an inclusion of finite groups,^[13] does not always remember the (core-free) inclusion.^[14][15]

A Bisch-Jones subfactor planar algebra ${\displaystyle {\mathcal {BJ}}(\delta _{1},\delta _{2})}$ (sometimes called Fuss-Catalan) is defined as for ${\displaystyle {\mathcal {TLJ}}(\delta )}$ but by allowing two colors of string with their own constant ${\displaystyle \delta _{1}}$ and ${\displaystyle \delta _{2}}$, with ${\displaystyle \delta _{i}}$ as above. It is a planar subalgebra of any subfactor planar algebra with an intermediate such that ${\displaystyle [K:N]=\delta _{1}^{2}}$ and ${\displaystyle [M:K]=\delta _{2}^{2}}$.^[16][17]

The first finite depth subfactor planar algebra of index ${\displaystyle \delta ^{2}>4}$ is called the Haagerup subfactor planar algebra.^[18] It has index ${\displaystyle (5+{\sqrt {13}})/2\sim 4.303}$.

The subfactor planar algebras are completely classified for index at most ${\displaystyle 5}$^[19] and a bit beyond.^[20] This classification was initiated by Uffe Haagerup.^[21] It uses (among other things) a listing of possible principal graphs, together with the embedding theorem^[22] and the jellyfish algorithm.^[23]

A subfactor planar algebra remembers the subfactor (i.e. its standard invariant is complete) if it is amenable.^[24] A finite depth hyperfinite subfactor is amenable.

About the non-amenable case: there are unclassifiably many irreducible hyperfinite subfactors of index 6 that all have the same standard invariant.^[25]

Fourier transform and biprojections

Let ${\displaystyle N\subset M}$ be a finite index subfactor, and ${\displaystyle {\mathcal {P}}}$ the corresponding subfactor planar algebra. Assume that ${\displaystyle {\mathcal {P}}}$ is irreducible (i.e. ${\displaystyle {\mathcal {P}}_{1,+}=N'\cap M_{1}=\mathbb {C} }$). Let ${\displaystyle N\subset K\subset M}$ be an intermediate subfactor. Let the Jones projection ${\displaystyle e_{K}^{M}:L^{2}(M)\to L^{2}(K)}$. Note that ${\displaystyle e_{K}^{M}\in {\mathcal {P}}_{2,+}}$. Let ${\displaystyle id:=e_{M}^{M}}$ and ${\displaystyle e_{1}:=e_{N}^{M}}$.

Note that ${\displaystyle tr(e_{1})=\delta ^{-2}=[M:N]^{-1}}$ and ${\displaystyle tr(id)=1}$.

Let the bijective linear map ${\displaystyle {\mathcal {F}}:{\mathcal {P}}_{2,\pm }\to {\mathcal {P}}_{2,\mp }}$ be the Fourier transform, also called ${\displaystyle 1}$-click (of the outer star) or ${\displaystyle 90^{\circ }}$ rotation; and let ${\displaystyle a*b}$ be the coproduct of ${\displaystyle a}$ and ${\displaystyle b}$.

Note that the word coproduct is a diminutive of convolution product. It is a binary operation.

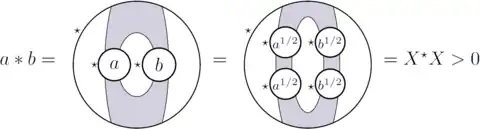
The coproduct satisfies the equality ${\displaystyle a*b={\mathcal {F}}({\mathcal {F}}^{-1}(a){\mathcal {F}}^{-1}(b)).}$

For any positive operators ${\displaystyle a,b}$, the coproduct ${\displaystyle a*b}$ is also positive; this can be seen diagrammatically:^[26]

Let ${\displaystyle {\overline {a}}:={\mathcal {F}}({\mathcal {F}}(a))}$ be the contragredient ${\displaystyle a}$ (also called ${\displaystyle 180^{\circ }}$ rotation). The map ${\displaystyle {\mathcal {F}}^{4}}$ corresponds to four ${\displaystyle 1}$-clicks of the outer star, so it's the identity map, and then ${\displaystyle {\overline {\overline {a}}}=a}$.

In the Kac algebra case, the contragredient is exactly the antipode,^[12] which, for a finite group, correspond to the inverse.

A biprojection is a projection ${\displaystyle b\in {\mathcal {P}}_{2,+}\setminus \{0\}}$ with ${\displaystyle {\mathcal {F}}(b)}$ a multiple of a projection. Note that ${\displaystyle e_{1}=e_{N}^{M}}$ and ${\displaystyle id=e_{M}^{M}}$ are biprojections; this can be seen as follows:

A projection ${\displaystyle b}$ is a biprojection iff it is the Jones projection ${\displaystyle e_{K}^{M}}$ of an intermediate subfactor ${\displaystyle N\subset K\subset M}$,^[27] iff ${\displaystyle e_{1}\leq b={\overline {b}}=\lambda b*b,{\text{ with }}\lambda ^{-1}=\delta tr(b)}$.^[28][26]

Galois correspondence:^[29] in the Kac algebra case, the biprojections are 1-1 with the left coideal subalgebras, which, for a finite group, correspond to the subgroups.

For any irreducible subfactor planar algebra, the set of biprojections is a finite lattice,^[30] of the form ${\displaystyle [e_{1},id]}$, as for an interval of finite groups ${\displaystyle [H,G]}$.

Using the biprojections, we can make the intermediate subfactor planar algebras.^[31][32]

The uncertainty principle extends to any irreducible subfactor planar algebra ${\displaystyle {\mathcal {P}}}$:

Let ${\displaystyle {\mathcal {S}}(x)=Tr(R(x))}$ with ${\displaystyle R(x)}$ the range projection of ${\displaystyle x}$ and ${\displaystyle Tr}$ the unnormalized trace (i.e. ${\displaystyle Tr=\delta ^{n}tr}$ on ${\displaystyle {\mathcal {P}}_{n,\pm }}$).

Noncommutative uncertainty principle:^[33] Let ${\displaystyle x\in {\mathcal {P}}_{2,\pm }}$, nonzero. Then

${\displaystyle {\mathcal {S}}(x){\mathcal {S}}({\mathcal {F}}(x))\geq \delta ^{2}}$

Assuming ${\displaystyle x}$ and ${\displaystyle {\mathcal {F}}(x)}$ positive, the equality holds if and only if ${\displaystyle x}$ is a biprojection. More generally, the equality holds if and only if ${\displaystyle x}$ is the bi-shift of a biprojection.