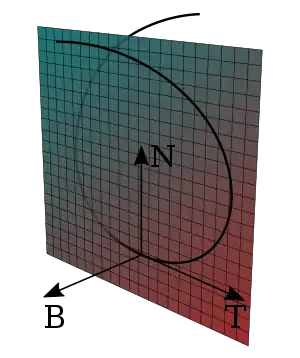
A space curve, Frenet–Serret frame, and the osculating plane (spanned by T and N).

In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a second order of contact at the point. The word osculate is from the Latin osculatus which is a past participle of osculari, meaning to kiss. An osculating plane is thus a plane which "kisses" a submanifold.

The osculating plane in the geometry of Euclidean space curves can be described in terms of the Frenet-Serret formulas as the linear span of the tangent and normal vectors.[1]

See also

References

  1. ↑ Do Carmo, Manfredo. Differential Geometry of Curves and Surfaces (2nd ed.). p. 18. ISBN 978-0486806990.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.