In mathematics, orthogonality is the generalization of the geometric notion of perpendicularity to the linear algebra of bilinear forms.

Two elements u and v of a vector space with bilinear form B are orthogonal when B(u, v) = 0. Depending on the bilinear form, the vector space may contain nonzero self-orthogonal vectors. In the case of function spaces, families of orthogonal functions are used to form a basis.

The concept has been used in the context of orthogonal functions, orthogonal polynomials, and combinatorics.

Orthogonality and rotation of coordinate systems compared between left: Euclidean space through circular angle ϕ, right: in Minkowski spacetime through hyperbolic angle ϕ (red lines labelled c denote the worldlines of a light signal, a vector is orthogonal to itself if it lies on this line).^[1]

Definitions

• In geometry, two Euclidean vectors are orthogonal if they are perpendicular, i.e., they form a right angle.
• Two vectors x and y in an inner product space V are orthogonal if their inner product ${\displaystyle \langle x,y\rangle }$ is zero.^[2] This relationship is denoted ${\displaystyle x\perp y}$.
• An orthogonal matrix is a matrix whose column vectors are orthonormal to each other.
• An orthonormal basis is a basis whose vectors are both orthogonal and normalized (they are unit vectors).
• A conformal linear transformation preserves angles and distance ratios, meaning that transforming orthogonal vectors by the same conformal linear transformation will keep those vectors orthogonal.
• Two vector subspaces A and B of an inner product space V are called orthogonal subspaces if each vector in A is orthogonal to each vector in B. The largest subspace of V that is orthogonal to a given subspace is its orthogonal complement.
• Given a module M and its dual M^∗, an element m′ of M^∗ and an element m of M are orthogonal if their natural pairing is zero, i.e., ⟨m′, m⟩ = 0. Two sets S′ ⊆ M^∗ and S ⊆ M are orthogonal if each element of S′ is orthogonal to each element of S.^[3]
• A term rewriting system is said to be orthogonal if it is left-linear and is non-ambiguous. Orthogonal term rewriting systems are confluent.

A set of vectors in an inner product space is called pairwise orthogonal if each pairing of them is orthogonal. Such a set is called an orthogonal set.

In certain cases, the word normal is used to mean orthogonal, particularly in the geometric sense as in the normal to a surface. For example, the y-axis is normal to the curve y = x² at the origin. However, normal may also refer to the magnitude of a vector. In particular, a set is called orthonormal (orthogonal plus normal) if it is an orthogonal set of unit vectors. As a result, use of the term normal to mean "orthogonal" is often avoided. The word "normal" also has a different meaning in probability and statistics.

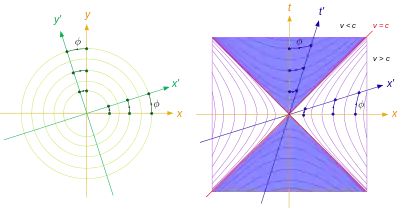
A vector space with a bilinear form generalizes the case of an inner product. When the bilinear form applied to two vectors results in zero, then they are orthogonal. The case of a pseudo-Euclidean plane uses the term hyperbolic orthogonality. In the diagram, axes x′ and t′ are hyperbolic-orthogonal for any given ϕ.

Euclidean vector spaces

In Euclidean space, two vectors are orthogonal if and only if their dot product is zero, i.e. they make an angle of 90° (π/2 radians), or one of the vectors is zero.^[4] Hence orthogonality of vectors is an extension of the concept of perpendicular vectors to spaces of any dimension.

The orthogonal complement of a subspace is the space of all vectors that are orthogonal to every vector in the subspace. In a three-dimensional Euclidean vector space, the orthogonal complement of a line through the origin is the plane through the origin perpendicular to it, and vice versa.^[5]

Note that the geometric concept of two planes being perpendicular does not correspond to the orthogonal complement, since in three dimensions a pair of vectors, one from each of a pair of perpendicular planes, might meet at any angle.

In four-dimensional Euclidean space, the orthogonal complement of a line is a hyperplane and vice versa, and that of a plane is a plane.^[5]

Orthogonal functions

By using integral calculus, it is common to use the following to define the inner product of two functions f and g with respect to a nonnegative weight function w over an interval [a, b]:

${\displaystyle \langle f,g\rangle _{w}=\int _{a}^{b}f(x)g(x)w(x)\,dx.}$

In simple cases, w(x) = 1.

We say that functions f and g are orthogonal if their inner product (equivalently, the value of this integral) is zero:

${\displaystyle \langle f,g\rangle _{w}=0.}$

Orthogonality of two functions with respect to one inner product does not imply orthogonality with respect to another inner product.

We write the norm with respect to this inner product as

${\displaystyle \|f\|_{w}={\sqrt {\langle f,f\rangle _{w}}}}$

The members of a set of functions {f_i : i = 1, 2, 3, ...} are orthogonal with respect to w on the interval [a, b] if

${\displaystyle \langle f_{i},f_{j}\rangle _{w}=0\quad i\neq j.}$

The members of such a set of functions are orthonormal with respect to w on the interval [a, b] if

${\displaystyle \langle f_{i},f_{j}\rangle _{w}=\delta _{i,j},}$

where

${\displaystyle \delta _{i,j}=\left\{{\begin{matrix}1,&&i=j\\0,&&i\neq j\end{matrix}}\right.}$

is the Kronecker delta. In other words, every pair of them (excluding pairing of a function with itself) is orthogonal, and the norm of each is 1. See in particular the orthogonal polynomials.

Examples

• The vectors (1, 3, 2)^T, (3, −1, 0)^T, (1, 3, −5)^T are orthogonal to each other, since (1)(3) + (3)(−1) + (2)(0) = 0, (3)(1) + (−1)(3) + (0)(−5) = 0, and (1)(1) + (3)(3) + (2)(−5) = 0.
• The vectors (1, 0, 1, 0, ...)^T and (0, 1, 0, 1, ...)^T are orthogonal to each other. The dot product of these vectors is 0. We can then make the generalization to consider the vectors in Z₂ⁿ:
  $${\displaystyle \mathbf {v} _{k}=\sum _{i=0 \atop ai+k<n}^{n/a}\mathbf {e} _{i}}$$

  
  for some positive integer a, and for 1 ≤ k ≤ a − 1, these vectors are orthogonal, for example ${\displaystyle {\begin{bmatrix}1&0&0&1&0&0&1&0\end{bmatrix}}}$, ${\displaystyle {\begin{bmatrix}0&1&0&0&1&0&0&1\end{bmatrix}}}$, ${\displaystyle {\begin{bmatrix}0&0&1&0&0&1&0&0\end{bmatrix}}}$ are orthogonal.
• The functions 2t + 3 and 45t² + 9t − 17 are orthogonal with respect to a unit weight function on the interval from −1 to 1:
  $${\displaystyle \int _{-1}^{1}\left(2t+3\right)\left(45t^{2}+9t-17\right)\,dt=0}$$

  
• The functions 1, sin(nx), cos(nx) : n = 1, 2, 3, ... are orthogonal with respect to Riemann integration on the intervals [0, 2π], [−π, π], or any other closed interval of length 2π. This fact is a central one in Fourier series.

Combinatorics

In combinatorics, two n×n Latin squares are said to be orthogonal if their superimposition yields all possible n² combinations of entries.^[6]

See also

Look up orthogonal in Wiktionary, the free dictionary.

• Imaginary number
• Isogonal
• Isogonal trajectory
• Orthogonal complement
• Orthogonal group
• Orthogonal matrix
• Orthogonal polynomials
• Orthogonalization
  • Gram–Schmidt process
• Orthonormal basis
• Orthonormality
• Orthogonal transform
• Pan-orthogonality occurs in coquaternions

References