an open set covering of the sierpinski triangle along with one of its mappings ψ_i.

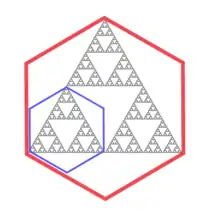
In fractal geometry, the open set condition (OSC) is a commonly imposed condition on self-similar fractals. In some sense, the condition imposes restrictions on the overlap in a fractal construction.^[1] Specifically, given an iterated function system of contractive mappings ${\displaystyle \psi _{1},\ldots ,\psi _{m}}$, the open set condition requires that there exists a nonempty, open set V satisfying two conditions:

1. ${\displaystyle \bigcup _{i=1}^{m}\psi _{i}(V)\subseteq V,}$
2. The sets ${\displaystyle \psi _{1}(V),\ldots ,\psi _{m}(V)}$ are pairwise disjoint.

Introduced in 1946 by P.A.P Moran,^[2] the open set condition is used to compute the dimensions of certain self-similar fractals, notably the Sierpinski Gasket. It is also used to simplify computation of the packing measure.^[3]

An equivalent statement of the open set condition is to require that the s-dimensional Hausdorff measure of the set is greater than zero.^[4]

Computing Hausdorff dimension

When the open set condition holds and each ${\displaystyle \psi _{i}}$ is a similitude (that is, a composition of an isometry and a dilation around some point), then the unique fixed point of ${\displaystyle \psi }$ is a set whose Hausdorff dimension is the unique solution for s of the following:^[5]

${\displaystyle \sum _{i=1}^{m}r_{i}^{s}=1.}$

where r_i is the magnitude of the dilation of the similitude.

With this theorem, the Hausdorff dimension of the Sierpinski gasket can be calculated. Consider three non-collinear points a₁, a₂, a₃ in the plane R² and let ${\displaystyle \psi _{i}}$ be the dilation of ratio 1/2 around a_i. The unique non-empty fixed point of the corresponding mapping ${\displaystyle \psi }$ is a Sierpinski gasket, and the dimension s is the unique solution of

${\displaystyle \left({\frac {1}{2}}\right)^{s}+\left({\frac {1}{2}}\right)^{s}+\left({\frac {1}{2}}\right)^{s}=3\left({\frac {1}{2}}\right)^{s}=1.}$

Taking natural logarithms of both sides of the above equation, we can solve for s, that is: s = ln(3)/ln(2). The Sierpinski gasket is self-similar and satisfies the OSC.

Strong open set condition

The strong open set condition (SOSC) is an extension of the open set condition. A fractal F satisfies the SOSC if, in addition to satisfying the OSC, the intersection between F and the open set V is nonempty.^[6] The two conditions are equivalent for self-similar and self-conformal sets, but not for certain classes of other sets, such as function systems with infinite mappings and in non-euclidean metric spaces.^[7][8] In these cases, SOCS is indeed a stronger condition.

See also

• Cantor set
• List of fractals by Hausdorff dimension
• Minkowski–Bouligand dimension
• Packing dimension

References