Multicritical points are special points in the parameter space of thermodynamic or other systems with a continuous phase transition. At least two thermodynamic or other parameters must be adjusted to reach a multicritical point. At a multicritical point the system belongs to a universality class different from the "normal" universality class.

A more detailed definition requires concepts from the theory of critical phenomena, a branch of physics that reached a very satisfying state in the 1970s.

Definition

The union of all the points of the parameter space for which the system is critical is called a critical manifold.

A critical curve terminating at a multicritical point (schematic).

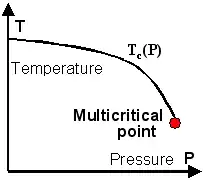
As an example consider a substance ferromagnetic below a transition temperature ${\displaystyle T_{c}}$, and paramagnetic above ${\displaystyle T_{c}}$. The parameter space here is the temperature axis, and the critical manifold consists of the point ${\displaystyle T_{c}}$. Now add hydrostatic pressure ${\displaystyle P}$ to the parameter space. Under hydrostatic pressure the substance normally still becomes ferromagnetic below a temperature ${\displaystyle T_{c}}$(${\displaystyle P}$).

This leads to a critical curve in the (${\displaystyle T,P}$) plane - a ${\displaystyle 1}$-dimensional critical manifold. Also taking into account shear stress ${\displaystyle K}$ as a thermodynamic parameter leads to a critical surface ${\displaystyle T_{c}}$(${\displaystyle P,K}$) in the (${\displaystyle T,P,K}$) parameter space - a ${\displaystyle 2}$-dimensional critical manifold. Critical manifolds of dimension ${\displaystyle d>1}$ and ${\displaystyle d>2}$ may have physically reachable borders of dimension ${\displaystyle d-1}$ which in turn may have borders of dimension ${\displaystyle d-2}$. The system still is critical at these borders. However, criticality terminates for good reason, and the points on the borders normally belong to another universality class than the universality class realized within the critical manifold. All the points on the border of a critical manifold are multicritical points. Instead of terminating somewhere critical manifolds also may branch or intersect. The points on the intersections or branch lines also are multicritical points.

At least two parameters must be adjusted to reach a multicritical point. A ${\displaystyle 2}$-dimensional critical manifold may have two ${\displaystyle 1}$-dimensional borders intersecting at a point. Two parameters must be adjusted to reach such a border, three parameters must be adjusted to reach the intersection of the two borders. A system of this type represents up to four universality classes: one within the critical manifold, two on the borders and one on the intersection of the borders.

The gas-liquid critical point is not multicritical, because the phase transition at the vapour pressure curve ${\displaystyle P}$(${\displaystyle T}$) is discontinuous and the critical manifold thus consists of a single point.

Examples

Lee-Yang edge singularity

The critical point of the Ising model with critical temperature ${\displaystyle T_{c}}$ ramifies into the two branches of the Lee-Yang critical manifold in an imaginary magnetic field ${\displaystyle H}$ for ${\displaystyle T>T_{c}}$ (schematic).

The critical manifold of an Ising model with zero external magnetic field consists of the point at the critical temperature ${\displaystyle T_{c}}$ on the temperature axis ${\displaystyle T}$. In a purely imaginary external magnetic field ${\displaystyle H}$ this critical manifold ramifies into the two branches of the Lee-Yang type, belonging to a different universality class.^[1] The Ising critical point plays the role of a multicritical point in this situation (there are no imaginary magnetic fields, but there are equivalent physical situations).

References