Logarithmic

Probability mass function 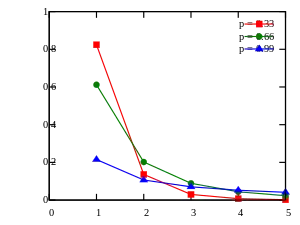Plot of the logarithmic PMF The function is only defined at integer values. The connecting lines are merely guides for the eye.
Cumulative distribution function 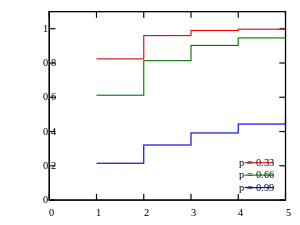Plot of the logarithmic CDF
Parameters	${\displaystyle 0<p<1}$
Support	${\displaystyle k\in \{1,2,3,\ldots \}}$
PMF	${\displaystyle {\frac {-1}{\ln(1-p)}}{\frac {p^{k}}{k}}}$
CDF	${\displaystyle 1+{\frac {\mathrm {B} (p;k+1,0)}{\ln(1-p)}}}$
Mean	${\displaystyle {\frac {-1}{\ln(1-p)}}{\frac {p}{1-p}}}$
Mode	${\displaystyle 1}$
Variance	${\displaystyle -{\frac {p^{2}+p\ln(1-p)}{(1-p)^{2}(\ln(1-p))^{2}}}}$
MGF	${\displaystyle {\frac {\ln(1-pe^{t})}{\ln(1-p)}}{\text{ for }}t<-\ln p}$
CF	${\displaystyle {\frac {\ln(1-pe^{it})}{\ln(1-p)}}}$
PGF	${\displaystyle {\frac {\ln(1-pz)}{\ln(1-p)}}{\text{ for }}|z|<{\frac {1}{p}}}$

In probability and statistics, the logarithmic distribution (also known as the logarithmic series distribution or the log-series distribution) is a discrete probability distribution derived from the Maclaurin series expansion

${\displaystyle -\ln(1-p)=p+{\frac {p^{2}}{2}}+{\frac {p^{3}}{3}}+\cdots .}$

From this we obtain the identity

${\displaystyle \sum _{k=1}^{\infty }{\frac {-1}{\ln(1-p)}}\;{\frac {p^{k}}{k}}=1.}$

This leads directly to the probability mass function of a Log(p)-distributed random variable:

${\displaystyle f(k)={\frac {-1}{\ln(1-p)}}\;{\frac {p^{k}}{k}}}$

for k ≥ 1, and where 0 < p < 1. Because of the identity above, the distribution is properly normalized.

The cumulative distribution function is

${\displaystyle F(k)=1+{\frac {\mathrm {B} (p;k+1,0)}{\ln(1-p)}}}$

where B is the incomplete beta function.

A Poisson compounded with Log(p)-distributed random variables has a negative binomial distribution. In other words, if N is a random variable with a Poisson distribution, and X_i, i = 1, 2, 3, ... is an infinite sequence of independent identically distributed random variables each having a Log(p) distribution, then

${\displaystyle \sum _{i=1}^{N}X_{i}}$

has a negative binomial distribution. In this way, the negative binomial distribution is seen to be a compound Poisson distribution.

R. A. Fisher described the logarithmic distribution in a paper that used it to model relative species abundance.^[1]

See also

• Poisson distribution (also derived from a Maclaurin series)

References

Further reading

• Johnson, Norman Lloyd; Kemp, Adrienne W; Kotz, Samuel (2005). "Chapter 7: Logarithmic and Lagrangian distributions". Univariate discrete distributions (3 ed.). John Wiley & Sons. ISBN 978-0-471-27246-5.
• Weisstein, Eric W. "Log-Series Distribution". MathWorld.