|
Probability density function 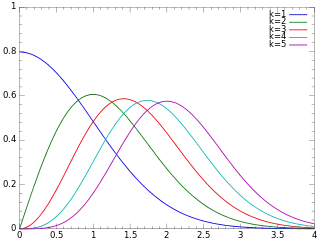 | |||
|
Cumulative distribution function 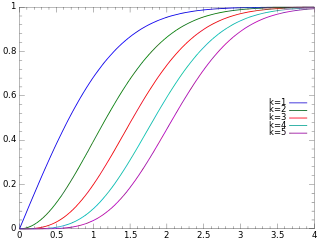 | |||
| Parameters | (degrees of freedom) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | for | ||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy |
| ||
| MGF | Complicated (see text) | ||
| CF | Complicated (see text) | ||
In probability theory and statistics, the chi distribution is a continuous probability distribution over the non-negative real line. It is the distribution of the positive square root of a sum of squared independent Gaussian random variables. Equivalently, it is the distribution of the Euclidean distance between a multivariate Gaussian random variable and the origin. It is thus related to the chi-squared distribution by describing the distribution of the positive square roots of a variable obeying a chi-squared distribution.
If are independent, normally distributed random variables with mean 0 and standard deviation 1, then the statistic
is distributed according to the chi distribution. The chi distribution has one positive integer parameter , which specifies the degrees of freedom (i.e. the number of random variables ).
The most familiar examples are the Rayleigh distribution (chi distribution with two degrees of freedom) and the Maxwell–Boltzmann distribution of the molecular speeds in an ideal gas (chi distribution with three degrees of freedom).
Definitions
Probability density function
The probability density function (pdf) of the chi-distribution is
where is the gamma function.
Cumulative distribution function
The cumulative distribution function is given by:
where is the regularized gamma function.
Generating functions
The moment-generating function is given by:
where is Kummer's confluent hypergeometric function. The characteristic function is given by:
Properties
Moments
The raw moments are then given by:
where is the gamma function. Thus the first few raw moments are:
where the rightmost expressions are derived using the recurrence relationship for the gamma function:
From these expressions we may derive the following relationships:
Mean: which is close to for large k.
Variance: which approaches as k increases.
Skewness:
Kurtosis excess:
Entropy
The entropy is given by:
where is the polygamma function.
Large n approximation
We find the large n=k+1 approximation of the mean and variance of chi distribution. This has application e.g. in finding the distribution of standard deviation of a sample of normally distributed population, where n is the sample size.
The mean is then:
We use the Legendre duplication formula to write:
- ,
so that:
Using Stirling's approximation for Gamma function, we get the following expression for the mean:
And thus the variance is:
Related distributions
- If then (chi-squared distribution)
- (Normal distribution)
- If then
- If then (half-normal distribution) for any
- (Rayleigh distribution)
- (Maxwell distribution)
- , the Euclidean norm of a standard normal random vector of with dimensions, is distributed according to a chi distribution with degrees of freedom
- chi distribution is a special case of the generalized gamma distribution or the Nakagami distribution or the noncentral chi distribution
- The mean of the chi distribution (scaled by the square root of ) yields the correction factor in the unbiased estimation of the standard deviation of the normal distribution.
| Name | Statistic |
|---|---|
| chi-squared distribution | |
| noncentral chi-squared distribution | |
| chi distribution | |
| noncentral chi distribution |