Kinematics of the cuboctahedron

The skeleton of a cuboctahedron, considering its edges as rigid beams connected at flexible joints at its vertices but omitting its faces, does not have structural rigidity and consequently its vertices can be repositioned by folding (changing the dihedral angle) at edges and face diagonals. The cuboctahedron's kinematics is noteworthy in that its vertices can be repositioned to the vertex positions of the regular icosahedron, the Jessen's icosahedron, and the regular octahedron, in accordance with the pyritohedral symmetry of the icosahedron.^[1]^[2]

Kinematic cuboctahedra

	Cuboctahedron	Regular icosahedron	Jessen's icosahedron	Regular octahedron
Coxeter mirrors
Mirror dihedrals	𝝅/4 𝝅/3 𝝅/2	𝝅/3 𝝅/5 𝝅/2	𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/4 𝝅/2

Rigid and kinematic cuboctahedra

Progressions between an octahedron, pseudoicosahedron, and cuboctahedron. The cuboctahedron can flex this way even if its edges (but not its faces) are rigid.

When interpreted as a framework of rigid flat faces, connected along the edges by hinges, the cuboctahedron is a rigid structure, as are all convex polyhedra, by Cauchy's theorem. However, when the faces are removed, leaving only rigid edges connected by flexible joints at the vertices, the result is not a rigid system (unlike polyhedra whose faces are all triangles, to which Cauchy's theorem applies despite the missing faces).

Adding a central vertex, connected by rigid edges to all the other vertices, subdivides the cuboctahedron into square pyramids and tetrahedra, meeting at the central vertex. Unlike the cuboctahedron itself, the resulting system of edges and joints is rigid, and forms part of the infinite octet truss structure.

Cyclical cuboctahedron transformations

The cuboctahedron can be transformed cyclically through four polyhedra, repeating the cycle endlessly. Topologically the transformation follows a Möbius loop: it is an orientable double cover of the octahedron.

In their spatial relationships the cuboctahedron, icosahedron, Jessen's icosahedron, and octahedron nest like Russian dolls and are related by a helical contraction.^{[lower-alpha 1]} The contraction^{[lower-alpha 2]} begins with the square faces of the cuboctahedron folding inward along their diagonals to form pairs of triangles.^{[lower-alpha 3]} The 12 vertices of the cuboctahedron spiral inward (toward the center) and move closer together until they reach the points where they form a regular icosahedron; they move slightly closer together until they form a Jessen's icosahedron; and they continue to spiral toward each other until they coincide in pairs as the 6 vertices of the octahedron.^[3]

The general cuboctahedron transformation can be parameterized along a continuum of special-case transformations with two limit-cases: one in which the edges of the cuboctahedron are rigid, and one in which they are elastic.

Rigid-edge transformation

Continuous transformation between the cuboctahedron and the octahedron pausing at the vertex position of the regular icosahedron. The vertex position of the Jessen's icosahedron lies between the regular icosahedron and the octahedron (but the animation does not pause there). This is an animation of the rigid-edge cuboctahedron transformation, not of the elastic-edge transformation: it does not illustrate the Jessen's icosahedron's long edges at all, and the short edges do not lengthen (as they do by 15% at the elastic-edge transformation's cuboctahedron and octahedron limit positions); instead, the (invisible) long edges shorten by 15% at the limit positions (in the elastic-edge transformation they are rigid). The passage of the Jessen's icosahedron point (important in the elastic-edge transformation because the short edges reach their minimum size and begin to lengthen again) is not visible at all. The helical contraction of the cuboctahedron into successively smaller-radius polyhedra is visible as it occurs in the rigid-edge cuboctahedron transformation (and in the elastic-edge transformation it would be quite similar).

The rigid-edge cuboctahedron transformation symmetrically transforms the cuboctahedron into a regular icosahedron, a Jessen's icosahedron, and a regular octahedron, in the sense that the polyhedron's vertices take on the vertex positions of those polyhedra successively.

The cuboctahedron does not actually become those other polyhedra, and they cannot transform into each other (if they have rigid edges), because unlike the cuboctahedron they do have structural rigidity as a consequence of having only triangular faces.

What the cuboctahedron with rigid edges actually can transform into (and through) is a regular icosahedron from which 6 edges are missing (a pseudoicosahedron),^[4] a Jessen's icosahedron in which the 6 reflex edges are missing or elastic,^{[lower-alpha 4]} and a double cover of the octahedron that has two coincident rigid edges connecting each pair of vertices (formed by making pairs of cuboctahedron vertices coincide).

Rigid-edge kinematic cuboctahedra

	Cuboctahedron	Regular icosahedron	Jessen's icosahedron	Regular octahedron
Edge	${\sqrt {6}}$	${\sqrt {6}}$	${\sqrt {6}}$	${\sqrt {6}}$
Chord	$2{\sqrt {3}}\approx 3.464$	$\left({\tfrac {1+{\sqrt {5}}}{2}}\right){\sqrt {6}}\approx 3.963$	$4$	$2{\sqrt {3}}\approx 3.464$
Chord radius	${\sqrt {3}}\approx 1.732$	${\tfrac {\sqrt {6}}{2}}\approx 1.225$	$1$	$0$
Long radius	${\sqrt {6}}\approx 2.449$	$\left({\tfrac {\sqrt {10+2{\sqrt {5}}}}{4}}\right){\sqrt {6}}\approx 2.330$	${\sqrt {5}}\approx 2.236$	${\sqrt {3}}\approx 1.732$

Elastic-edge transformation

There is a tensegrity polyhedron which embodies and enforces the closely related elastic-edge cuboctahedron transformation. The tensegrity icosahedron has a dynamic structural rigidity called infinitesimal mobility and can only be deformed into symmetrical polyhedra along that spectrum from cuboctahedron to octahedron.^[5] It is called the tensegrity icosahedron because its median stable form is the Jessen's icosahedron.

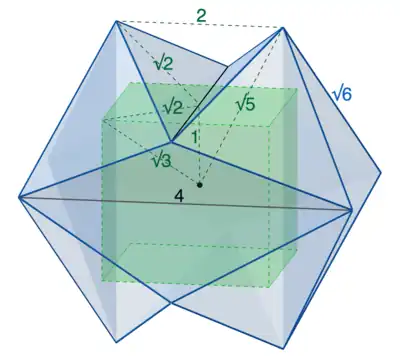
Jessen's icosahedron. All dihedral angles are 90°. The vertices of the inscribed cube are the centers of the equilateral triangle faces. The polyhedron is a construct of the lengths √1 √2 √3 √4 √5 √6 and the angles 𝝅2 𝝅3 𝝅4.

Although the transformation is described above as a contraction of the cuboctahedron, the stable equilibrium point of the tensegrity is the Jessen's icosahedron;^[6] the tensegrity icosahedron resists being deformed from that shape and can only be forced to expand or contract from it to the extent that its edges are elastic (able to lengthen under tension). Forcing the polyhedron away from its stable resting shape (in either direction) involves stretching its 24 short edges slightly and equally.^{[lower-alpha 5]} Force applied to any pair of parallel long edges, to move them closer together or farther apart, is transferred automatically to stretch all the short edges uniformly,^{[lower-alpha 6]} shrinking the polyhedron from its medium-size Jessen's icosahedron toward the smaller octahedron, or expanding it toward the larger regular icosahedron and still larger cuboctahedron, respectively.^{[lower-alpha 7]} Releasing the force causes the polyhedron to spring back to its Jessen's icosahedron resting shape.^{[lower-alpha 8]}

In the elastic-edge transformation the cuboctahedron edges are not rigid (though the Jessen's icosahedron's 6 long edges are).^{[lower-alpha 9]} What the cuboctahedron actually transforms into is a regular icosahedron of shorter radius and shorter edge length, a Jessen's icosahedron of still shorter radius and (minimum) edge length, and finally an octahedron of still shorter radius but the same (maximum) edge length as the cuboctahedron (but only after the edges have shortened and lengthened again, and come together in coincident pairs).

Elastic-edge kinematic cuboctahedra

	Cuboctahedron	Regular icosahedron	Jessen's icosahedron	Regular octahedron
Edge	$2{\sqrt {2}}\approx 2.828$	${\tfrac {8}{1+{\sqrt {5}}}}\approx 2.472$	${\sqrt {6}}\approx 2.449$	$2{\sqrt {2}}\approx 2.828$
Chord	$4$	$4$	$4$	$4$
Chord radius	$2$	${\tfrac {4}{1+{\sqrt {5}}}}\approx 1.236$	$1$	$0$
Long radius	$2{\sqrt {2}}\approx 2.828$	${\tfrac {2{\sqrt {10+2{\sqrt {5}}}}}{1+{\sqrt {5}}}}\approx 2.351$	${\sqrt {5}}\approx 2.236$	$2$

Duality of the rigid-edge and elastic-edge transformations

The rigid-edge and elastic-edge cuboctahedron transformations differ only in having reciprocal parameters: in the elastic-edge transformation the Jessen's icosahedron's short edges stretch and its long edges are rigid, and in the rigid-edge transformation its long edges compress and its short edges are rigid. Everything in the descriptions above except the metrics applies to all cuboctahedron transformations. In particular, the vertices always move in helices toward the center as the cuboctahedron transforms into the octahedron,^[9]^[10] and the Jessen's icosahedron (with 90° dihedral angles) is always the median point, stable to the extent that there is resistance to the stretching or compressing.^[11]

The elastic-edge cuboctahedron transformation is usually given as the mathematics of the tensegrity icosahedron^[12] because it comes closest to modeling how most actual tensegrity icosahedron structures behave. However, one could certainly construct a tensegrity icosahedron in which the short edges (cables) were perfectly inelastic, and the long edges (struts) were compressable springs. Such a tensegrity would perform the rigid-edge cuboctahedron transformation.

Finally, both transformations are pure abstractions, the two limit cases of an infinite family of cuboctahedron transformations in which there are two elasticity parameters and no requirement that one of them be 0. Neither limit case is apt to apply perfectly to most real tensegrity structures, which usually have some elasticity in both the cables and the struts, giving their actual behavior metrics which are non-trivial to calculate.^[13] In engineering practice, only a tiny amount of elasticity is required to allow a significant degree of motion, so most tensegrity structures are constructed to be "drum-tight" using nearly inelastic struts and cables. A tensegrity icosahedron transformation is a kinematic cuboctahedron transformation with reciprocal small elasticity parameters.

Jitterbug transformations

The twisting, expansive-contractive transformations between these polyhedra were named Jitterbug transformations by Buckminster Fuller. Fuller did not give any mathematics;^[14]^[15] like many great geometers before him (Alicia Boole Stott for example) he did not have any mathematics to give. But he was the first to stress the importance of the cuboctahedron's radial equilateral symmetry which he applied structurally (and patented) as the octet truss, intuiting that it plays a fundamental role not only in structural integrity but in the dimensional relationships between polytopes. He discovered the kinematic transformation of the cuboctahedron, understood its relationship to the tensegrity icosahedron, and even gave demonstrations of the rigid-edge cuboctahedron transformation before audiences (in the days before computer-rendered animations). His demonstration with commentary of the "vector equilibrium",^[16] as he called the cuboctahedron, is still far more illuminating than the animations in this article.

Notes

↑ A static instance of this nesting of these polyhedra occurs in the 600-cell regular 4-polytope.
↑ The cuboctahedron radius is √2 times the octahedron radius.
↑ Notice that the contraction is chiral, since there are two choices of diagonal on which to begin folding the square faces. The red-and-yellow animation in this article cycles endlessly through the same chiral form of the rigid-edge cuboctahedron transformation. It could (but does not) cycle through both chiral forms of the rigid-edge transformation alternately, departing from the cuboctahedron by folding the opposite set of square face diagonals each time. This would take it all the way around the topological Mobius loop each time it traversed both chiral forms. But instead, it reverses at the limit cases (cuboctahedron and octahedron), and endlessly shuffles back and forth along the same half of the Mobius loop, never setting foot on the other half of it. Watch the blue-and-white animation carefully and see if you can tell if it is doing the same thing, or if it is performing the entire rigid-edge cuboctahedron transformation.
↑ The Jessen's icosahedron's long reflex edges have length 4d where d is their mid-edge-to-center distance. In the rigid-edge cuboctahedron transformation the rigid-edge length is √6d, and the reflex edge chords shorten from 4d to 2√3d at both the cuboctahedron limit (where they are the diagonals of the square faces) and at the regular octahedron limit (where they are the long diameter).
↑ The Jessen's icosahedron has only 8 of the regular icosahedron's 20 equilateral triangle faces and 24 of its 30 edges, but it also has 12 isosceles triangle faces that meet in pairs at 6 longer edges (its reflex edges which lie in concave troughs). The 6 long edges occur as 3 orthogonal pairs of parallel edges on opposite sides of the polyhedron, and in their resting state each parallel pair is exactly as far apart as 1/2 their length; each resting long edge lies 1/4 its length from the center, defined as the unit short radius (so the long edge length is 4, and their distance apart at rest is 2). In the resting state the short edge length is √6 ≈ 2.449, and the long radius (center to vertex) is √5 ≈ 2.236. The altitude of the isosceles triangles at rest is √2 ≈ 1.414, and the long radius of the polyhedron expands by the product of √2: in the elastic-edge transformation from 2 at the octahedron limit of contraction to 2√2 at the cuboctahedron limit of expansion, where the cuboctahedron's radius is also its edge length (it is radially equilateral).
↑ The force places the long edges under compression load like columns, not tension load like the short edges. Unlike the elastic short edges which stretch and lengthen slightly, the long edges must resist compression perfectly and not shorten.
↑ Forcing any pair of parallel long edges slightly apart expands the polyhedron, forcing all 3 pairs apart similarly until they become chords of the regular icosahedron, at which point the √6 ≈ 2.449 short edges have stretched only ~1% to a length of 4/ϕ ≈ 2.472. If the short edges are elastic enough that they can be stretched ~15% to 2√2 ≈ 2.828 the long edges will become the square face diagonals of the cuboctahedron (at the limit of expansion).
↑ Forcing any pair of parallel long edges toward each other contracts the polyhedron, forcing all 3 pairs toward each other similarly until they coincide and become the 3 orthogonal axes of the regular octahedron. At that point (the limit of contraction) the √6 ≈ 2.449 short edges have also stretched (not contracted!) to their limit length of 2√2 ≈ 2.828, and now coincide in pairs as the 12 edges of the regular octahedron.
↑ The vertices of the regular icosahedron form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings. In a Jessen's icosahedron of unit short radius one set of these three rectangles (the set in which the Jessen's icosahedron's long edges are the rectangles' long edges) measures $2\times 4$ . These three rectangles are the shortest possible representation of the Borromean rings using only edges of the integer lattice.^[7]

References

↑ Gunn & Sullivan 2008, §3. Pyritohedral Symmetry; "The pyritohedral 3D symmetry group is the unique polyhedral point group that is neither a rotation group nor a reflection group."
↑ Koca et al. 2016, p. 145, 4. Pyritohedral Group and Related Polyhedra; see Table 1.
↑ Coxeter 1973, pp. 50–52, §3.7: Coordinates for the vertices of the regular and quasi-regular solids; describes the cuboctahedron transformation in Euclidean 3-space; separately (pp=150-152, §8 Truncations) Coxeter also describes its 4-dimensional analogue, in which the cuboctahedron transforms in the curved 3-space of the 3-sphere embedded in Euclidean 4-space; that kinematics is beyond the scope of this article, except to note that it includes a further stage of the cuboctahedron transformation (which is not reached in the tensegrity icosahedron transformations described in this article): from the octahedron the vertices continue moving along the same helical paths, separating again into the 12 vertices of the snub octahedron (a smaller regular icosahedron nested inside the octahedron).
↑ Koca et al. 2016, 4.1 Construction of the vertices of the pseudoicosahedron.
↑ Kenner 1976, pp. 11–19, §2. Spherical tensegrities.
↑ Fuller 1975, cuboctahedron as vector equilibrium, a completely unstable condition; as Buckminster Fuller was the first to realize, the cuboctahedron is the antipodal unstable equilibrium point of the cycle. At that point, as at an airplane's stall point, multiple kinematics can happen: the polyhedron can depart the cuboctahedron in either direction along the cycle, folding on either set of square diagonals to select either of two chiral subcycles (connected in a single Möbius loop). In an actual tensegrity structure this nondeterministic choice does not occur, often because the cuboctahedron limit position is never actually reached; even when it is, the structure is constrained by the struts to one chiral form.
↑ Uberti, R.; Janse van Rensburg, E. J.; Orlandini, E.; Tesi, M. C.; Whittington, S. G. (1998), "Minimal links in the cubic lattice", in Whittington, Stuart G.; Sumners, Witt De; Lodge, Timothy (eds.), Topology and Geometry in Polymer Science, IMA Volumes in Mathematics and its Applications, vol. 103, New York: Springer, pp. 89–100, doi:10.1007/978-1-4612-1712-1_9, MR 1655039; see Table 2, p. 97
↑ Clinton, J.D. (1971). "A geometric transformation concept for expanding rigid structures". NASA Report: Advanced structural geometry studies, Part 2. Vol. CR-1735. Washington, D.C.: Southern Ill. Univ.
↑ Verheyen 1989, p. 203; "As Clinton observed in his paper on expanding rigid structures^[8], each triangle is subject to a translation-rotation along its symmetry axis. When starting from the position in the octahedron, these axes are the four triangular symmetry axes of the octahedron. When describing cylinders about the triangles along the axes, each vertex common to two triangles moves along the intersecting [helical] curve of the two cylinders."
↑ Itoh & Nara 2021, p. 13, §4. From the 24-cell onto an octahedron; "Lemma 4.2. There is a continuous motion of Q (the cuboctahedron without square faces) shown in Fig. 5a onto the octahedron W⁰ satisfying the following conditions for each face F of Q, e.g. F = 𝚫a₁a₂a₃. (1) F is rotated and moved toward along the line l joining the centroids of F and 𝚫v₁v₂v₃. (2) F always touches the cylinder T(F), that is, F is always orthogonal to l."
↑ Kenner 1976, p. 14, Equilibrium.
↑ Kenner 1976, pp. 16–17, Elasticity Multiplication.
↑ Kenner 1976, p. 12, Equilibrium.
↑ Verheyen 1989.
↑ Itoh & Nara 2021, Abstract; "This article addresses the 24-cell and gives a continuous flattening motion for its 2-skeleton [the cuboctahedron], which is related to the Jitterbug by Buckminster Fuller."
↑ Fuller 1975, Fuller carefully folds a model of the cuboctahedron made of rigid struts with flexible joints through the entire rigid-edge transformation cycle; in this film, he does not demonstrate the elastic-edge transformation (which he observed in the tensegrity icosahedron), but he does show how a rigid regular icosahedron can be rotated inside an inscribing "vector edge cube" (a cube with an octahedron inscribed in it), keeping the 12 vertices on the surface of the cube (and on the edges of the octahedron inscribed in the cube) at all times; actually, Fuller could have rotated any of the kinematic polyhedra in an inscribing cube in this way: the entire cuboctahedron transformation cycle takes place inside an inscribing cube of varying edge length, with the 12 vertices always on the surface of the cube.

Bibliography

Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
Fuller, R. Buckminster (1975). "Vector Equilibrium". Everything I Know Sessions. Philadelphia.
Kenner, Hugh (1976). Geodesic Math and How to Use It. University of California Press. ISBN 978-0520029248.
Verheyen, H. F. (1989). "The complete set of Jitterbug transformers and the analysis of their motion". Computers and Mathematics with Applications. 17 (1–3): 203–250. doi:10.1016/0898-1221(89)90160-0. MR 0994201.
Itoh, Jin-ichi; Nara, Chie (2021). "Continuous flattening of the 2-dimensional skeleton of a regular 24-cell". Journal of Geometry. 112 (13). doi:10.1007/s00022-021-00575-6.
Gunn, Charles; Sullivan, John M. (2008), "The Borromean Rings: A video about the New IMU logo", in Sarhangi, Reza; Séquin, Carlo H. (eds.), Bridges Leeuwarden: Mathematics, Music, Art, Architecture, Culture, London: Tarquin Publications, pp. 63–70, ISBN 978-0-9665201-9-4; see the video itself at "The Borromean Rings: A new logo for the IMU", International Mathematical Union
Koca, Nazife; Al-Mukhaini, Aida; Koca, Mehmet; Al Qanobi, Amal (2016-12-01). "Symmetry of the Pyritohedron and Lattices". Sultan Qaboos University Journal for Science [SQUJS]. 21: 139. doi:10.24200/squjs.vol21iss2pp139-149.

External links

"Borromean Rings". International Mathematical Union.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[3] A static instance of this nesting of these polyhedra occurs in the 600-cell regular 4-polytope.

[4] The cuboctahedron radius is √2 times the octahedron radius.

[5] Notice that the contraction is chiral, since there are two choices of diagonal on which to begin folding the square faces. The red-and-yellow animation in this article cycles endlessly through the same chiral form of the rigid-edge cuboctahedron transformation. It could (but does not) cycle through both chiral forms of the rigid-edge transformation alternately, departing from the cuboctahedron by folding the opposite set of square face diagonals each time. This would take it all the way around the topological Mobius loop each time it traversed both chiral forms. But instead, it reverses at the limit cases (cuboctahedron and octahedron), and endlessly shuffles back and forth along the same half of the Mobius loop, never setting foot on the other half of it. Watch the blue-and-white animation carefully and see if you can tell if it is doing the same thing, or if it is performing the entire rigid-edge cuboctahedron transformation.

[8] The Jessen's icosahedron's long reflex edges have length 4d where d is their mid-edge-to-center distance. In the rigid-edge cuboctahedron transformation the rigid-edge length is √6d, and the reflex edge chords shorten from 4d to 2√3d at both the cuboctahedron limit (where they are the diagonals of the square faces) and at the regular octahedron limit (where they are the long diameter).

[11] The Jessen's icosahedron has only 8 of the regular icosahedron's 20 equilateral triangle faces and 24 of its 30 edges, but it also has 12 isosceles triangle faces that meet in pairs at 6 longer edges (its reflex edges which lie in concave troughs). The 6 long edges occur as 3 orthogonal pairs of parallel edges on opposite sides of the polyhedron, and in their resting state each parallel pair is exactly as far apart as 1/2 their length; each resting long edge lies 1/4 its length from the center, defined as the unit short radius (so the long edge length is 4, and their distance apart at rest is 2). In the resting state the short edge length is √6 ≈ 2.449, and the long radius (center to vertex) is √5 ≈ 2.236. The altitude of the isosceles triangles at rest is √2 ≈ 1.414, and the long radius of the polyhedron expands by the product of √2: in the elastic-edge transformation from 2 at the octahedron limit of contraction to 2√2 at the cuboctahedron limit of expansion, where the cuboctahedron's radius is also its edge length (it is radially equilateral).

[12] The force places the long edges under compression load like columns, not tension load like the short edges. Unlike the elastic short edges which stretch and lengthen slightly, the long edges must resist compression perfectly and not shorten.

[13] Forcing any pair of parallel long edges slightly apart expands the polyhedron, forcing all 3 pairs apart similarly until they become chords of the regular icosahedron, at which point the √6 ≈ 2.449 short edges have stretched only ~1% to a length of 4/ϕ ≈ 2.472. If the short edges are elastic enough that they can be stretched ~15% to 2√2 ≈ 2.828 the long edges will become the square face diagonals of the cuboctahedron (at the limit of expansion).

[14] Forcing any pair of parallel long edges toward each other contracts the polyhedron, forcing all 3 pairs toward each other similarly until they coincide and become the 3 orthogonal axes of the regular octahedron. At that point (the limit of contraction) the √6 ≈ 2.449 short edges have also stretched (not contracted!) to their limit length of 2√2 ≈ 2.828, and now coincide in pairs as the 12 edges of the regular octahedron.

[16] The vertices of the regular icosahedron form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings. In a Jessen's icosahedron of unit short radius one set of these three rectangles (the set in which the Jessen's icosahedron's long edges are the rectangles' long edges) measures $2\times 4$ . These three rectangles are the shortest possible representation of the Borromean rings using only edges of the integer lattice.^[7]

[FOOTNOTEGunnSullivan2008§3._Pyritohedral_Symmetry-1] Gunn & Sullivan 2008, §3. Pyritohedral Symmetry; "The pyritohedral 3D symmetry group is the unique polyhedral point group that is neither a rotation group nor a reflection group."

[FOOTNOTEKocaAl-MukhainiKocaAl_Qanobi20161454._Pyritohedral_Group_and_Related_Polyhedra-2] Koca et al. 2016, p. 145, 4. Pyritohedral Group and Related Polyhedra; see Table 1.

[FOOTNOTECoxeter197350–52§3.7:_Coordinates_for_the_vertices_of_the_regular_and_quasi-regular_solids-6] Coxeter 1973, pp. 50–52, §3.7: Coordinates for the vertices of the regular and quasi-regular solids; describes the cuboctahedron transformation in Euclidean 3-space; separately (pp=150-152, §8 Truncations) Coxeter also describes its 4-dimensional analogue, in which the cuboctahedron transforms in the curved 3-space of the 3-sphere embedded in Euclidean 4-space; that kinematics is beyond the scope of this article, except to note that it includes a further stage of the cuboctahedron transformation (which is not reached in the tensegrity icosahedron transformations described in this article): from the octahedron the vertices continue moving along the same helical paths, separating again into the 12 vertices of the snub octahedron (a smaller regular icosahedron nested inside the octahedron).

[FOOTNOTEKocaAl-MukhainiKocaAl_Qanobi20164.1_Construction_of_the_vertices_of_the_pseudoicosahedron-7] Koca et al. 2016, 4.1 Construction of the vertices of the pseudoicosahedron.

[FOOTNOTEKenner197611–19§2._Spherical_tensegrities-9] Kenner 1976, pp. 11–19, §2. Spherical tensegrities.

[FOOTNOTEFuller1975cuboctahedron_as_vector_equilibrium,_a_completely_unstable_condition-10] Fuller 1975, cuboctahedron as vector equilibrium, a completely unstable condition; as Buckminster Fuller was the first to realize, the cuboctahedron is the antipodal unstable equilibrium point of the cycle. At that point, as at an airplane's stall point, multiple kinematics can happen: the polyhedron can depart the cuboctahedron in either direction along the cycle, folding on either set of square diagonals to select either of two chiral subcycles (connected in a single Möbius loop). In an actual tensegrity structure this nondeterministic choice does not occur, often because the cuboctahedron limit position is never actually reached; even when it is, the structure is constrained by the struts to one chiral form.

[lattice-15] Uberti, R.; Janse van Rensburg, E. J.; Orlandini, E.; Tesi, M. C.; Whittington, S. G. (1998), "Minimal links in the cubic lattice", in Whittington, Stuart G.; Sumners, Witt De; Lodge, Timothy (eds.), Topology and Geometry in Polymer Science, IMA Volumes in Mathematics and its Applications, vol. 103, New York: Springer, pp. 89–100, doi:10.1007/978-1-4612-1712-1_9, MR 1655039; see Table 2, p. 97

[17] Clinton, J.D. (1971). "A geometric transformation concept for expanding rigid structures". NASA Report: Advanced structural geometry studies, Part 2. Vol. CR-1735. Washington, D.C.: Southern Ill. Univ.

[FOOTNOTEVerheyen1989203-18] Verheyen 1989, p. 203; "As Clinton observed in his paper on expanding rigid structures^[8], each triangle is subject to a translation-rotation along its symmetry axis. When starting from the position in the octahedron, these axes are the four triangular symmetry axes of the octahedron. When describing cylinders about the triangles along the axes, each vertex common to two triangles moves along the intersecting [helical] curve of the two cylinders."

[FOOTNOTEItohNara202113§4._From_the_24-cell_onto_an_octahedron;_"Lemma_4.2-19] Itoh & Nara 2021, p. 13, §4. From the 24-cell onto an octahedron; "Lemma 4.2. There is a continuous motion of Q (the cuboctahedron without square faces) shown in Fig. 5a onto the octahedron W⁰ satisfying the following conditions for each face F of Q, e.g. F = 𝚫a₁a₂a₃. (1) F is rotated and moved toward along the line l joining the centroids of F and 𝚫v₁v₂v₃. (2) F always touches the cylinder T(F), that is, F is always orthogonal to l."

[FOOTNOTEKenner197614Equilibrium-20] Kenner 1976, p. 14, Equilibrium.

[FOOTNOTEKenner197616–17Elasticity_Multiplication-21] Kenner 1976, pp. 16–17, Elasticity Multiplication.

[FOOTNOTEKenner197612Equilibrium-22] Kenner 1976, p. 12, Equilibrium.

[FOOTNOTEVerheyen1989-23] Verheyen 1989.

[FOOTNOTEItohNara2021Abstract-24] Itoh & Nara 2021, Abstract; "This article addresses the 24-cell and gives a continuous flattening motion for its 2-skeleton [the cuboctahedron], which is related to the Jitterbug by Buckminster Fuller."

[FOOTNOTEFuller1975Fuller_carefully_folds_a_model_of_the_cuboctahedron_made_of_rigid_struts_with_flexible_joints_through_the_entire_''rigid-edge''_transformation_cycle-25] Fuller 1975, Fuller carefully folds a model of the cuboctahedron made of rigid struts with flexible joints through the entire rigid-edge transformation cycle; in this film, he does not demonstrate the elastic-edge transformation (which he observed in the tensegrity icosahedron), but he does show how a rigid regular icosahedron can be rotated inside an inscribing "vector edge cube" (a cube with an octahedron inscribed in it), keeping the 12 vertices on the surface of the cube (and on the edges of the octahedron inscribed in the cube) at all times; actually, Fuller could have rotated any of the kinematic polyhedra in an inscribing cube in this way: the entire cuboctahedron transformation cycle takes place inside an inscribing cube of varying edge length, with the 12 vertices always on the surface of the cube.

[1]

[2]

[lower-alpha 1]

[lower-alpha 2]

[lower-alpha 3]

[3]

[4]

[lower-alpha 4]

[5]

[6]

[lower-alpha 5]

[lower-alpha 6]

[lower-alpha 7]

[lower-alpha 8]

[lower-alpha 9]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[7]

[8]