The astroid, constructed as an envelope of lines. The corresponding support function ranges from a minimum of 0 for the points on the horizontal and vertical axes to a maximum at the four diagonal points on the unit circle.

A hypocycloid that forms a self-crossing hedgehog

In differential geometry, a hedgehog or plane hedgehog is a type of plane curve, the envelope of a family of lines determined by a support function. More intuitively, sufficiently well-behaved hedgehogs are plane curves with one tangent line in each oriented direction. A projective hedgehog is a restricted type of hedgehog, defined from an anti-symmetric support function, and (again when sufficiently well-behaved) forms a curve with one tangent line in each direction, regardless of orientation.

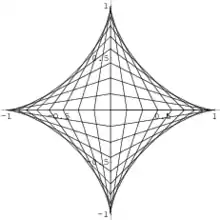
Every closed strictly convex curve, the envelope of its supporting lines. The astroid forms a non-convex hedgehog, and the deltoid curve forms a projective hedgehog.

Hedgehogs can also be defined from support functions of hyperplanes in higher dimensions.

Definitions

Formally, a planar support function can be defined as a continuously differentiable function ${\displaystyle h}$ from the unit circle in the plane to real numbers, or equivalently as a function ${\displaystyle f(\theta )=h{\bigl (}(\cos \theta ,\sin \theta ){\bigr )}}$ from angles to real numbers. For each point ${\displaystyle q}$ on the unit circle, it defines a line, the set of points ${\displaystyle p}$ for which ${\displaystyle p\cdot q=h(q)}$. This line is perpendicular to vector ${\displaystyle q}$, passes through the point ${\displaystyle qh(q)}$, and is at distance ${\displaystyle |h(q)|}$ from the origin. A support function is anti-symmetric when, for all ${\displaystyle q}$, ${\displaystyle h(-q)=-h(q)}$, or equivalently in terms of angles ${\displaystyle f(\theta )=-f(\theta +\pi )}$, so that ${\displaystyle q}$ and ${\displaystyle -q}$ define the same line as each other.^[1]

Given any support function ${\displaystyle h}$, its hedgehog is denoted ${\displaystyle {\mathcal {H}}_{h}}$. In terms of the function ${\displaystyle f}$ and the angle ${\displaystyle \theta }$ it has the parametric equations^[1]

${\displaystyle {\begin{aligned}x&=f(\theta )\cos \theta -f'(\theta )\sin \theta \\y&=f(\theta )\sin \theta +f'(\theta )\cos \theta \end{aligned}}}$

A hedgehog is non-singular when it has a tangent line at each of its points. A projective hedgehog is defined by an anti-symmetric support function. Hedgehogs can also be defined in the same way in higher dimensions, as envelopes of hyperplanes defined by support functions.^[2][3]

Examples

The support function describing the supporting lines for a convex set ${\displaystyle K}$ is defined by ${\displaystyle h(q)=\max\{p\cdot q\mid p\in K\}}$. The hedgehog of the support function of any strictly convex set is its boundary, parameterized by the angle of its supporting lines.^[4] When a convex set is not strictly convex (it has a line segment in its boundary), its support function is continuous but not continuously differentiable, and the parametric equations above jump discontinuously across the line segment instead of defining a continuous curve, so it is not defined as a hedgehog. The astroid provides an example of a non-convex hedgehog.^[5]

The deltoid, an example of a projective hedgehog, showing line segments rotating through the family of lines whose envelope is the deltoid

An example of a projective hedgehog, defined from an anti-symmetric support function, is given by the deltoid curve. The deltoid is a simple closed curve but other hedgehogs may self-intersect, or otherwise behave badly. In particular, there exist anti-symmetric support functions based on the Weierstrass function whose corresponding projective hedgehogs are fractal curves that are continuous but nowhere differentiable and have infinite length.^[4]

A Reuleaux triangle and its middle hedgehog, the locus of midpoints of its diameter segments. Although this hedgehog resembles a deltoid, it is not one; instead, it is formed from three circular arcs with half the radius of the outer arcs of the Reuleaux triangle.

Every strictly convex body in the plane defines a projective hedgehog, its middle hedgehog, the envelope of lines halfway between each pair of parallel supporting lines. Although triangles are not strictly convex, the envelope defined in this way for a triangle is its medial triangle. The points of the middle hedgehog are the midpoints of line segments connecting the pairs of points where each pair of parallel supporting lines contact the body. It has finite length, equal to half the perimeter of the given body. Each extreme point of the convex hull of the middle hedgehog is a convexity point, a point such that the union of the body with its reflection through this point is convex. There are always at least three such points, and the triangles and Reuleaux triangle provide examples where there are exactly three.^[6]

Properties

A non-singular hedgehog has a unique tangent line in each oriented direction, belonging to its defining family of lines. Correspondingly, any sufficiently well-behaved projective hedgehog has a unique tangent line in each direction without respect to orientation.

Pairs of hedgehogs can be combined by the pointwise sum of their support functions. This operation extends Minkowski addition of convex bodies and is analogous to Minkowski addition in multiple ways.^[7] It can be used to characterize curves of constant width: a convex hedgehog has constant width ${\displaystyle w}$ if and only if its support function is formed by adding ${\displaystyle w/2}$ to the support function of a projective hedgehog. That is, the curves of constant width are exactly the convex hedgehogs formed as sums of projective hedgehogs and circles.^[1]

Every projective hedgehog has at least three singularities (typically, cusps). When a projective hedgehog has finite length, a construction of Leonhard Euler shows that its involutes of sufficiently high radius are curves of constant width.^[8]

Generalization

More generally, hedgehogs are the natural geometrical objects that represent the formal differences of convex bodies: given (K,L) an ordered pair of convex bodies in the Euclidean vector space ℝⁿ⁺¹, there exists one, and only one, hedgehog that represents the formal difference K – L in ℝⁿ⁺¹.

Polygonal case in the plane:

Case of smooth convex bodies with positive Gauss curvature:

Subtracting two convex hypersurfaces (with positive Gauss curvature) by subtracting the points corresponding to a same outer unit normal to obtain a (possibly singular and self-intersecting) hypersurface:

The idea of using Minkowski differences of convex bodies may be traced back to a couple of papers by A.D. Alexandrov and H. Geppert^[9] in the 1930s. Many classical notions for convex bodies extend to hedgehogs and quite a number of classical results find their counterparts. Of course, a few adaptations are necessary. In particular, volumes have to be replaced by their algebraic versions.^[10]

In a long series of papers, hedgehogs and their extensions were studied by Y. Martinez-Maure under various aspects.^[11] The most striking result of this hedgehog theory was the construction of counterexamples to an old conjectured characterization of the 2-sphere.^{[12][13][14][15][10]}

References