| Crossed square cupola | |
|---|---|
 | |
| Type | Johnson isomorph Cupola |
| Faces | 4 triangles 1+4 squares 1 octagram |
| Edges | 20 |
| Vertices | 12 |
| Vertex configuration | 4+4(3.4.8/3) 4(3/2.43) |
| Schläfli symbol | {4/3} || t{4/3} |
| Symmetry group | C4v, [4], (*44) |
| Rotation group | C4, [4]+, (44) |
| Dual polyhedron | - |
In geometry, the crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.
It may be seen as a cupola with a retrograde square base, so that the squares and triangles connect across the bases in the opposite way to the square cupola, hence intersecting each other.
Related polyhedra
| {n/d} | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |  {4/3} Crossed square cupola |
 {5/3} Crossed pentragrammic cupola |
 {7/3} Heptagrammic cupola |
 {8/3} Octagrammic cupola |
| 5 | — | — |  {7/5} Crossed heptagrammic cupola |
 {8/5} Crossed octogrammic cupola |
The crossed square cupola may be seen as a part of some uniform polyhedra. For example, the great cubicuboctahedron may be seen as six crossed square cupolae connected at their triangular faces, while the nonconvex great rhombicuboctahedron may be seen as a blend of six cupolae. Additionally, the nonconvex great rhombicuboctahedron may be seen as an octagrammic prism with the octagrams excavated with crossed square cupolae, similarly to how the rhombicuboctahedron may be seen as an octagonal prism with the octagons augmented with square cupolae. Rotating one of the cupolae in this construction results in the pseudo-great rhombicuboctahedron. To this may be added the great rhombihexahedron, as the exclusive or of all three of these octagrammic prisms which may be used to construct the nonconvex great rhombicuboctahedron.
 Crossed square cupola |
 Nonconvex great rhombicuboctahedron |
 Pseudo-great rhombicuboctahedron |
 Great cubicuboctahedron |
 Great rhombihexahedron |
The pictures below show the excavation of the octagrammic prism with crossed square cupolae taking place one step at a time. The crossed square cupolae are always red, while the square sides of the octagrammic prism are in the other colours. All images are oriented approximately the same way for clarity.
 The octagrammic prism (coloured with D8h symmetry)... |
 ...with one of the octagrams (here, the top one) excavated with a crossed square cupola. This may be termed the retroelongated crossed square cupola or augmented octagrammic prism, and is isomorphic to the Johnson elongated square cupola. |
 There are two choices on the orientation of the other crossed square cupola. One aligns corresponding faces (triangles with triangles, squares with squares) and produces the nonconvex great rhombicuboctahedron. This construction has D4h symmetry, although the nonconvex great rhombicuboctahedron has full octahedral symmetry. |
 The other choice aligns noncorresponding faces (triangles with squares) and produces the pseudo-great rhombicuboctahedron (or pseudoquasirhombicuboctahedron). This construction has D4d symmetry. |
This series of excavations may be easily compared to the corresponding series of augmentations of the octagonal prism:
 The octagonal prism (coloured with D8h symmetry)... |
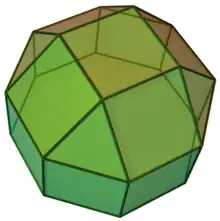 ...with one of the octagons augmented with a square cupola. |
 There are two choices on the orientation of the other crossed square cupola. One aligns corresponding faces (triangles with triangles, squares with squares) and produces the rhombicuboctahedron. This construction has D4h symmetry, although the rhombicuboctahedron has full octahedral symmetry. |
 The other choice aligns noncorresponding faces (triangles with squares) and produces the pseudorhombicuboctahedron. This construction has D4d symmetry. |
Dual polyhedron
The dual of the crossed square cupola has 8 triangular and 4 kite faces:

Due to faces of the crossed square cupola passing close to its centre, this dual is very spiky in appearance. This also occurs for the dual uniform polyhedra known as the great pentakis dodecahedron (DU58) and medial inverted pentagonal hexecontahedron (DU60).
References
- Jim McNeill, Cupola OR Semicupola
- Jim McNeill, Relation of Cupolas to Uniform Polyhedra