Bicorn

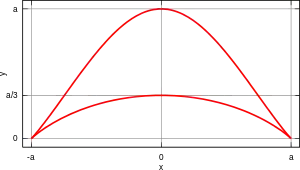
In geometry, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne, is a rational quartic curve defined by the equation^[1]

$${\displaystyle y^{2}\left(a^{2}-x^{2}\right)=\left(x^{2}+2ay-a^{2}\right)^{2}.}$$

It has two cusps and is symmetric about the y-axis.^[2]

History

In 1864, James Joseph Sylvester studied the curve

$${\displaystyle y^{4}-xy^{3}-8xy^{2}+36x^{2}y+16x^{2}-27x^{3}=0}$$

in connection with the classification of quintic equations; he named the curve a bicorn because it has two cusps. This curve was further studied by Arthur Cayley in 1867.^[3]

Properties

A transformed bicorn with a = 1

The bicorn is a plane algebraic curve of degree four and genus zero. It has two cusp singularities in the real plane, and a double point in the complex projective plane at x=0, z=0. If we move x=0 and z=0 to the origin substituting and perform an imaginary rotation on x bu substituting ix/z for x and 1/z for y in the bicorn curve, we obtain

$${\displaystyle \left(x^{2}-2az+a^{2}z^{2}\right)^{2}=x^{2}+a^{2}z^{2}.}$$

This curve, a limaçon, has an ordinary double point at the origin, and two nodes in the complex plane, at x = ± i and z = 1.^[4]

The parametric equations of a bicorn curve are

$${\displaystyle x=a\sin(\theta )}$$

and

$${\displaystyle y=a{\frac {\cos ^{2}(\theta )\left(2+\cos(\theta )\right)}{3+\sin ^{2}(\theta )}}}$$

with ${\displaystyle -\pi \leq \theta \leq \pi }$.

See also

• List of curves

References

External links

• Weisstein, Eric W. "Bicorn". MathWorld.