Twierdzenie Brianchona, Sześciokąt opisany na elipsie

Twierdzenie Brianchona (czyt. Briãszona) – twierdzenie opisujące pewną własność sześciokąta opisanego na krzywej stożkowej. Udowodnił je francuski matematyk Charles Julien Brianchon. Twierdzenie jest prawdziwe w geometrii afinicznej i rzutowej. Jest ono dualne do twierdzenia Pascala, co oznacza, że twierdzenia te są równoważne.

Treść

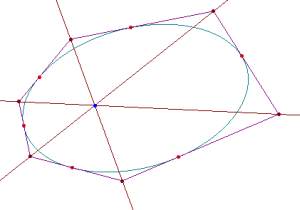
Dla każdego sześciokąta opisanego na dowolnej krzywej stożkowej trzy odcinki łączące ich przeciwległe wierzchołki przecinają się w jednym punkcie.

Twierdzenie zachodzi też, gdy wierzchołki sześciokąta połączymy innymi prostymi tak, żeby każdy z nich należał do dokładnie jednej z trzech prostych.

Dowód

Ponieważ twierdzenie dotyczy geometrii rzutowej, przypadki sześciokątów opisanych na innych niż okrąg krzywych stożkowych można sprowadzić rzutowo do przypadku z okręgiem. Pozostaje udowodnić ten przypadek.

Rys. 1. – Czerwone i zielone odcinki mają odpowiednio te same długości.

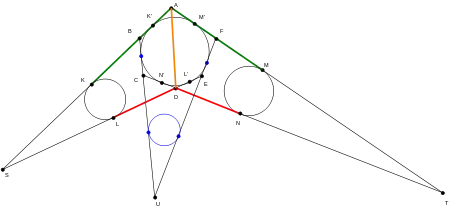
Przedłużamy boki sześciokąta jak na rys. 1.

Weźmy dowolny okrąg styczny do ${\displaystyle l_{DE}}$ i ${\displaystyle l_{AB}.}$

Oznaczmy punkty styczności przez ${\displaystyle K,L,}$ zaś przecięcie prostych przez ${\displaystyle S.}$

Niech ${\displaystyle K',\ L'}$ będą punktami styczności boków ${\displaystyle DE,\ AB}$ sześciokąta z okręgiem wpisanym.

${\displaystyle SK=SL}$ oraz ${\displaystyle SK'=SL',}$ bo są to styczne poprowadzone parami z tego samego punktu do tego samego okręgu.

Stąd ${\displaystyle KK'=LL'.}$

Zatem możemy skonstruować taki okrąg styczny do ${\displaystyle l_{CD}}$ i ${\displaystyle l_{FA}}$ w punktach ${\displaystyle M,\ N,}$ że ${\displaystyle MM'=NN'=KK'=LL'.}$

Ponieważ ${\displaystyle DN'=DL'}$ oraz ${\displaystyle AK'=AM',}$ to ${\displaystyle LD=DN}$ (czerwone na rysunku) oraz ${\displaystyle KA=AM}$ (zielone).

Rys. 2. – Niebieskie odcinki mają równe długości. Każda przekątna jest prostą potęgową tych dwóch z kolorowych okręgów, które są innego koloru niż ona.

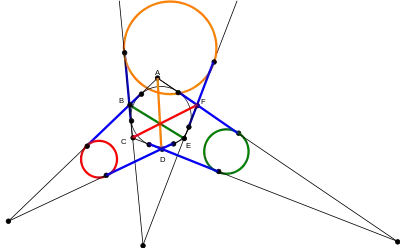
Zatem ${\displaystyle l_{AD}}$ jest prostą potęgową dwóch okręgów.

Podobnie pokazujemy, że pozostałe przekątne sześciokąta są prostymi potęgowymi odpowiednich okręgów (rys. 2).

Okręgi ustawiamy tak, żeby niebieskie odcinki (łączące ich punkty styczności z przedłużeniami boków sześciokąta oraz punkty styczności boków sześciokąta z okręgiem wpisanym) miały równe długości, oraz żeby do niebieskich odcinków należały wierzchołki ${\displaystyle B,\ D,\ F,}$ zaś nie należały wierzchołki ${\displaystyle A,\ C,\ E.}$ Wtedy długości odpowiednich stycznych są sumami lub różnicami odpowiednich odcinków tak, że faktycznie przekątne są prostymi potęgowymi.

Dla trzech okręgów proste potęgowe par okręgów są współpękowe, więc teza twierdzenia została udowodniona.

Zobacz też

• twierdzenie Pascala