Paproć Barnsleya

Paproć Barnsleya

Przekształcenia IFS

Paproć Barnsleya (paprotka Barnsleya, fraktal liść paproci) – fraktal znany ze względu na uderzające podobieństwo do liści paproci występujących w naturze, spopularyzowany przez Michaela F. Barnsleya. Jest to przykład złożonego obiektu, który może być opisany za pomocą zaledwie czterech przekształceń afinicznych (zob. Barnsley (1993), s. 86) jako atraktor następującego systemu funkcji zwężających (IFS – system funkcji iterowanych):

${\displaystyle f_{1}(x,y)=(0.85x+0.04y,-0.04x+0.85y+1.6)}$

${\displaystyle f_{2}(x,y)=(-0.15x+0.28y,0.26x+0.24y+0.44)}$

${\displaystyle f_{3}(x,y)=(0.20x-0.26y,0.23x+0.22y+1.6)}$

${\displaystyle f_{4}(x,y)=(0,0.16y).}$

Aby wygenerować fraktal, należy użyć powyższych przekształceń w sposób losowy w następujących proporcjach: 85:7:7:1.

Algorytm

Algorytm generowania tego fraktala polega na procesie iteracji (wielokrotnego przekształcania) współrzędnych rysowanego punktu. Początkowo losowo wybiera się współrzędne punktu, a następnie również losowo wybiera się jedno z przekształceń afinicznych z odpowiednim prawdopodobieństwem. Po obliczeniu nowych współrzędnych punktu, proces powtarza się określoną liczbę razy.

Przykładowy programy (Matlab)

Animacja przedstawiająca paproć Barnsleya dla różnej liczby powtórzeń algorytmu IFS

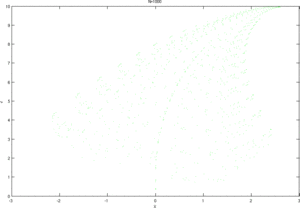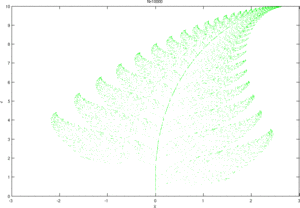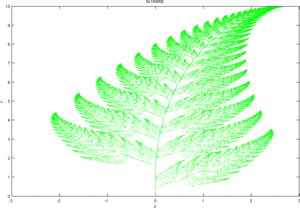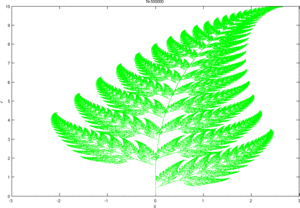
Program napisany w Matlabie generujący paproć widoczną na animacji obok:

for max_step=[1000 10000 50000  100000  500000];
    x=zeros(1,max_step);
    y=zeros(1,max_step);
    for n=1:max_step
        r=rand();
        if r<=0.01
            x(n+1)=0;
            y(n+1)=0.16*y(n);
        elseif r<=0.08
            x(n+1)=0.2*x(n)-0.26*y(n);
            y(n+1)=0.23*x(n)+0.22*y(n)+1.6;
        elseif r<=0.15
            x(n+1)=-0.15*x(n)+0.28*y(n);
            y(n+1)=0.26*x(n)+0.24*y(n)+0.44;
        else
            x(n+1)=0.85*x(n)+0.04*y(n);
            y(n+1)=-0.04*x(n)+ 0.85*y(n)+1.6;
        end
    end
    plot(x,y,'.','Color', 'g', 'MarkerSize',1)
    title(['N = ' num2str(max_step)])
    drawnow
    pause(0.5)
end

Literatura

• Barnsley, Michael F., and Hawley Rising. Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0.

Zobacz też

• fraktal
• grafika fraktalna
• przekształcenie afiniczne

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Barnsley's Fern, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).