Ruch paczki trojańskiej – gęstość prawdopodobieństwa elektronu w czasie

Paczka trojańska lub trojańska paczka falowa (ang. Trojan wave packet lub Trojan Wavepackets) – w mechanice kwantowej stan stacjonarny hamiltonianu Starka-Zeemana, który jest również pakietem falowym w układzie współrzędnych nie poruszającym się względem obserwatora. Źródło silnego promieniowania cyklotronowego o częstotliwości optycznej lub mikrofalowej.

Paczka trojańska jest generowana podczas wzbudzania rozrzedzonego gazu wodorowego w silnym polu lasera lub mikrofal. Obserwacja paczki trojańskiej wiąże się z obserwacją przewidywań atomu Bohra w laboratorium fizycznym. Jest ona także przykładem poprawności twierdzenia Ehrenfesta, wyjaśniającego tzw. zasadę korespondencji pomiędzy mechaniką klasyczną i kwantową, tzn. dlaczego normalnie niewidzialna mechanika kwantowa posiada granicę klasyczną postrzeganą na co dzień. Paczka trojańska została po raz pierwszy zaobserwowana w eksperymencie w 2004 na Uniwersytecie Wirginii w USA na wysoce ekscentrycznej orbicie eliptycznej, a w 2009 w oryginalnej konfiguracji na orbicie kołowej poprzez rozszerzanie tej orbity eliptycznej adiabatyczną zmianą polaryzacji mikrofal z liniowej do kołowej.

Paczka trojańska jest również przykładem kwantowego stanu Glaubera lub inaczej stanu koherentnego, dla elektronu, a nie dla pola elektromagnetycznego, za którego odkrycie i znaczenie w teorii światła spójnego przyznano w 2005 roku nagrodę Nobla z fizyki. Ściślej odpowiada ona światłu spójnemu w ściśniętym stanie koherentnym spolaryzowanemu kołowo.

Podstawy modelu

Symulacja klasyczna paczki trojańskiej na komputerze ZX Spectrum. Funkcja falowa paczki przybliżona jest przez zbiór (100) punktów rozrzuconych początkowo wewnątrz elipsy przypominającej kształtem paczkę (maksymalny region lokalizacji) i poruszających się zgodnie z równaniami Hamiltona (Newtona). Mechanika kwantowa wprowadzona jest do symulacji we współrzędnych skalowanych jedynie w postaci wielkości początkowej elipsy rozmycia warunków początkowych (im mniejsze tym wyższa liczba kwantowa). Rozmycie w chwili zero odpowiada średniej liczbie kwantowej paczki około n=400. Dla zademonstrowania znaczenia rotującego pola potrzebnego do lokalizacji po pięciu okresach obiegu paczki następuje wyświetlenie symulacji pięciu okresów bez pola kiedy to „paczka” złożona z punktów rozpływa się całkowicie po okręgu dookoła jądra. Film pokazuje symulację w znacznie przyśpieszonym tempie, w rzeczywistości trwa około 15 godzin. Kolory punktów nie mają znaczenia.

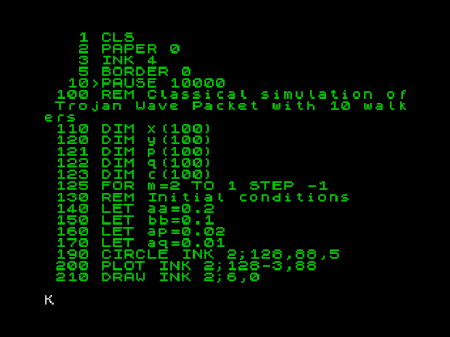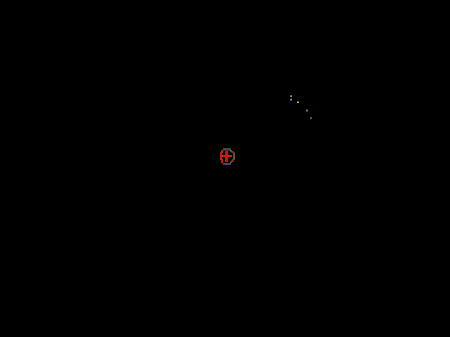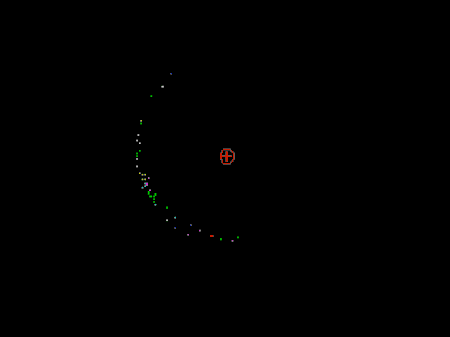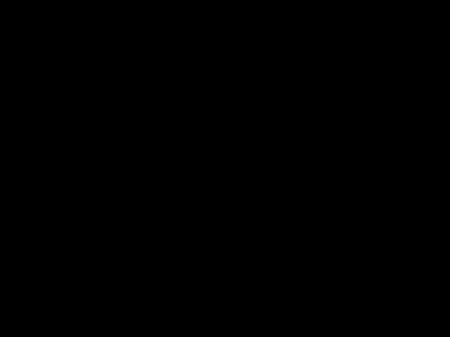
Ponieważ paczka trojańska jest przybliżonym stanem własnym hamiltonianu jej poszukiwanie zaczyna się od równania Schrödingera dla atomu wodoru w polu fali spolaryzowanej kołowo w układzie współrzędnych obracającym się z częstością fali

${\displaystyle {\hat {H}}\Psi =E\Psi ,}$

gdzie:

${\displaystyle {\hat {H}}={\frac {\hat {\boldsymbol {p}}}{2}}^{2}-{\frac {1}{r}}-\epsilon {\hat {x}}-\omega {\hat {L}}_{z}}$

i ${\displaystyle L_{z}}$ jest operatorem z-towej składowej momentu pędu.

Dla uproszczenia można ograniczyć się tylko do dwóch wymiarów przestrzennych. Równanie to po pominięciu członów krzywizny laplasjanu i założeniu wolnoznozmienności, a stałości niektórych członów przybiera wtedy we współrzędnych biegunowych uproszczoną, odseparowaną postać

${\displaystyle \left[-{\frac {\partial ^{2}}{2\partial r^{2}}}+{\frac {l^{2}}{2r^{2}}}-{\frac {1}{r}}-\epsilon r-{\frac {\partial ^{2}}{2r_{0}^{2}\partial \phi ^{2}}}-\epsilon r_{0}\cos \phi +\epsilon r_{0}\right]\chi =E\chi ,}$

${\displaystyle \chi =\mathrm {e} ^{\mathrm {i} l\phi }\Psi ,l=\omega ^{2}r_{0},}$

gdzie ${\displaystyle \hbar =1,m_{\mathrm {e} }=1,}$ a ${\displaystyle r_{0}}$ jest punktem minimum potencjału części hamiltonianu zależnej od współrzędnej radialnej i dlatego promieniem orbity klasycznej. Ponieważ potencjał radialny ma minimum paczka trojańska jest w tej teorii iloczynem dobrze zlokalizowanej radialnej funkcji Gaussa i dobrze zlokalizowanego wzbudzonego stanu wahadła matematycznego, odpowiadającej stanowi wahadła odwróconego do góry będącego funkcją Mathieu o wartości charakterystycznej (i energii) równej w dobrym przybliżeniu ${\displaystyle r_{0}\epsilon .}$ Bardziej dokładna teoria pokazuje, że jest to wahadło o ujemnej masie równej –1/3 masy elektronu i dlatego jest to jego stan podstawowy o takiej samej energii w odwróconym spektrum.

Aby to zauważyć zatrzymajmy jeszcze poprawkę z rozwinięcia członu odśrodkowego

${\displaystyle \Delta {\hat {H}}=-2\mathrm {i} {\frac {l}{r_{0}^{3}}}{\frac {\partial }{\partial \phi }}(r-r_{0})}$

i rozważmy jej działanie na składową Fouriera ${\displaystyle \chi }$ np. ${\displaystyle \mathrm {e} ^{\mathrm {i} k}.}$

Dodatkowy potencjał odśrodkowy będzie równy wtedy:

${\displaystyle \Delta V=2\mathrm {i} {\frac {l}{r_{0}^{3}}}k(r-r_{0}).}$

Wywoła on przesunięcie minimum i obniżenie energii radialnego oscylatora harmonicznego o:

${\displaystyle \Delta E=-{\frac {2}{r_{0}^{2}}}k^{2}.}$

Zastępując z powrotem ${\displaystyle k^{2}}$ operatorem z-towej składowej momentu pędu, otrzymujemy:

${\displaystyle \Delta {\hat {H}}={\frac {2\partial ^{2}}{r_{0}^{2}\partial \phi ^{2}}}.}$

Dodając tę poprawkę w równaniu Schrödingera, otrzymujemy równanie z ujemną i ułamkową masą elektronu –1/3 ${\displaystyle (m_{\mathrm {e} }){:}}$

${\displaystyle \left[-{\frac {\partial ^{2}}{2\partial r^{2}}}+{\frac {l^{2}}{2r^{2}}}-{\frac {1}{r}}-{\epsilon }r+{\frac {3\partial ^{2}}{2r_{0}^{2}\partial \phi ^{2}}}-\epsilon r_{0}\cos \phi +\epsilon r_{0}\right]\chi =E\chi ,}$

umożliwiającą gaussowską lokalizacje elektronu w maksimum, a nie w minimum potencjału w kierunku kątowym.

Paczka trojańska w modelu atomu dwupoziomowego

Ruch paczki trojańskiej – Gęstość prawdopodobieństwa elektronu w czasie dla paczki trojańskiej zlożonej ze stanu podstawowego i pierwszego stanu wzbudzonego atomu wodoru o głównej liczbie kwantowej ${\displaystyle n=2}$ i maksymalnym, zgodnym z polaryzacją pola momencie pędu, ${\displaystyle l=m=1.}$

Zjawisko paczki trojańskiej można wyjaśnić już w najbardziej znanym w optyce kwantowej przybliżeniu dwóch poziomów kwantowych. Widoczne zarzewie ruchu po orbicie kołowej jest wynikiem interferencji dwóch funkcji trygonometrycznych: sinus i cosinus będących czynnikiem stanu wzbudzonego. Jej dalsza lokalizacja względem wielkości orbity jest efektem małości odwrotności głównej liczby kwantowej atomu wodoru ${\displaystyle n,}$ tzn. ${\displaystyle 1/n.}$ Równanie Schrödingera w bazie dwóch poziomów kwantowych, tzn. stanu podstawowego n=1 i pierwszego wzbudzonego ${\displaystyle n=2=l+1=m+1}$ przybiera prostą postać macierzową ${\displaystyle 2\times 2{:}}$

${\displaystyle {\begin{bmatrix}E_{1}&\epsilon d\\\epsilon d&E_{1}\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}=E{\begin{bmatrix}a\\b\end{bmatrix}},}$

gdzie:

${\displaystyle d={\frac {128}{243}}a_{0}}$

z rozwiązaniami

${\displaystyle |\chi 1\rangle =(|0,0,0\rangle +|2,1,1\rangle )/{\sqrt {2}}}$

${\displaystyle E(1)=E_{1}+d\epsilon }$

${\displaystyle |\chi 2\rangle =(|0,0,0\rangle -|2,1,1\rangle )/{\sqrt {2}}}$

${\displaystyle E(2)=E_{1}-d\epsilon .}$

Stałość elementów diagonalnych macierzy jest wynikiem dokładnego rezonansu z polem, tzn. ${\displaystyle E_{2}-E_{1}=\omega .}$ Równanie to ma dwa rozwiązania z których stan o wyższej energii to paczka trojańska, a o niższej tzw. paczka antytrojańska. Energie w funkcji pola są liniami prostymi o przeciwnym współczynniku kierunkowym. W odróżnieniu od limitu dużych liczb kwantowych kształt stanu kwantowego nie zależy od wielkości pola, tzn. wodór w tych stanach ma stały rotujący moment dipolowy nawet dla pola znikającego podobnie jak w zwykłym statycznym efekcie Starka.

Ponieważ rozwiązanie to jest stacjonarne w układzie współrzędnych obracającym się, a funkcja falowa stanu wzbudzonego ${\displaystyle n=2}$ zawiera wykładnik kąta azymutalnego elektronu, wektory Blocha paczki trojańskiej i anty trojańskiej w układzie laboratoryjnym poruszają się z przesunięciem fazowym ${\displaystyle \pi }$ też po okręgu będącym równikiem sfery Blocha, tzn. dla paczki trojańskiej jego współrzędne są

${\displaystyle x=\cos \omega t}$

${\displaystyle y=\sin \omega t}$

${\displaystyle z=0}$

a

${\displaystyle x=-\cos \omega t}$

${\displaystyle y=-\sin \omega t}$

${\displaystyle z=0}$

dla paczki antytrojańskiej.

Planetoidy trojańskie

Paczka trojańska z punktu widzenia mechaniki klasycznej jest przeskalowaną wersją planetoid trojańskich, kiedy to pole fali elektromagnetycznej odpowiada Jowiszowi, proton wodoru Słońcu, a asteroidy gęstości prawdopodobieństwa elektronu. Z powodu braku krzywizny stałego pola elektrycznego w porównaniu z polem grawitacyjnym dwie grupy asteroid redukują się do jednej paczki.

Paczka trojańska i stany Landaua

Warto zauważyć, że podobne paczki falowe można uzyskać w dwóch wymiarach przestrzennych już w samym jednorodnym polu magnetycznym poprzez rozpędzenie tzw. stanu Landaua, stanu własnego elektronu odpowiadającego za kwantowy efekt Halla tak, aby poruszał się on po cyklotronowym okręgu. Najniższy stan Landaua jako stan własny oscylatora harmonicznego o częstości cyklotronowej odpowiada symetrycznemu, zlokalizowanemu stanowi Gaussa.

Ściśle równanie Schrödingera z Hamiltonianem Landaua elektronu w polu magnetycznym ${\displaystyle B}$

${\displaystyle {\hat {H}}={\frac {1}{2m}}{{\hat {p}}_{x}}^{2}+{\frac {1}{2m}}{{\hat {p}}_{y}}^{2}-{\frac {\omega _{\mathrm {c} }}{2}}{\hat {L}}_{z}+{\frac {\omega _{\mathrm {c} }^{2}}{8}}({\hat {x}}^{2}+{\hat {y}}^{2}),}$

${\displaystyle \omega _{\mathrm {c} }=eB/m,}$

może być zinterpretowane jako równanie dla oscylatora harmonicznego o częstości ${\displaystyle \omega _{\mathrm {c} }/2}$ i w układzie obracającym się z częstością ${\displaystyle \omega _{\mathrm {c} }/2}$ z powodu członu z ${\displaystyle L_{z}.}$ Stany koherentne tego oscylatora które są przesuniętym stanem podstawowym i które mogą poruszać się też po okręgu z częstością oscylatora ${\displaystyle \omega _{\mathrm {c} }/2}$ są nierozpływającymi się paczkami falowymi w układzie stacjonarnym poruszającymi się z częstością cyklotronową ${\displaystyle \omega _{\mathrm {c} }{:}}$

${\displaystyle \Psi (x,y,t)=C(t)\mathrm {e} ^{\mathrm {i} mr_{\mathrm {c} }\omega _{\mathrm {c} }/2\hbar (-x\sin \omega _{\mathrm {c} }t+y\cos \omega _{\mathrm {c} }t)}\mathrm {e} ^{-\beta ^{2}[(x-r_{c}\cos \omega _{\mathrm {c} }t)^{2}+(y-r_{\mathrm {c} }\sin \omega _{\mathrm {c} }t)^{2}]/2},}$

${\displaystyle \beta ^{2}=m\omega _{\mathrm {c} }/2\hbar .}$

Rozpędzony „trojański” stan Landaua. Podobnie jak paczka trojańska stan ten porusza się po orbicie kołowej o promieniu cyklotronowym ${\displaystyle r_{\mathrm {c} }}$ z częstością cyklotronową ${\displaystyle \omega _{\mathrm {c} }}$ i może być dowolnie wąsko zlokalizowany względem promienia orbity proporcjonalnie do natężenia pola magnetycznego. W odróżnieniu od paczki trojańskiej stan ten istnieje tylko w dwóch wymiarach przestrzennych, nie wymaga pola fali spolaryzowanej kołowo oraz jest symetryczny wokoło środka lokalizacji.

Dodanie potencjału kulombowskiego atomu wodoru w środku okręgu spowoduje wtedy dodatkową lokalizację w trzecim wymiarze w kierunku osi ${\displaystyle z}$ a dodanie pola fali spolaryzowanej kołowo zmieni jeszcze bardziej promień orbity i częstość obiegu. Zgodnie z twierdzeniem Ehrenfesta centrum takiego „Gausonu” będzie poruszać się po orbicie klasycznej po okręgu pod działaniem siły Lorentza, siły Coulomba i siły od rotującego pola. Paczka trojańska odpowiada wtedy granicy znikającego do zera stałego pola magnetycznego prostopadłego do płaszczyzny ruchu.

Paczka trojańska i kwantowy efekt Halla

Paczka trojańska umożliwia obserwacje efektu analogicznego do kwantowego efekt Halla, płynnie zmieniając częstość pola spolaryzowanego kołowo zamiast pola magnetycznego. Ruch pojedynczego elektronu po okręgu można interpretować jako prąd Halla podczas kiedy napięcie pomiędzy jądrem wodoru a elektronem jako wyindukowane napięcie Halla ponieważ jest ono prostopadłe do tego prądu. I rzeczywiście definiując

${\displaystyle I=\omega e/2\pi ,}$

${\displaystyle U=\epsilon r_{0},}$

otrzymamy w punktach dokładnego rezonansu

${\displaystyle r_{0n}=n^{2}a_{0},}$

${\displaystyle \omega _{n}=2R_{\infty }/n^{3}\hbar ,}$

kwantowanie oporu przy pomocy oporu podstawowego

${\displaystyle R_{n}=U/I=\epsilon _{\mathrm {sc} }{\frac {h}{e^{2}}}n^{5}=\epsilon _{\mathrm {sc} }n^{5}\;25812,807557\;\Omega ,}$

gdzie zdefiniowaliśmy bezwymiarowe pole elektryczne jako współczynnik proporcjonalności do pola w odległości promienia Bohra:

${\displaystyle \epsilon ={\frac {1}{4\pi \epsilon _{0}}}{\frac {e}{a_{0}^{2}}}\epsilon _{\mathrm {sc} }.}$

W odróżnieniu od normalnego kwantowego efektu Halla opór podstawowy jest dowolnie strojony polem.

Alternatywnie napięcie Halla można zdefiniować względem potencjału Coulomba, a nie pola zewnętrznego jako różnice potencjałów Coulomba pochodzących od jądra na orbicie paczki Trojańskiej i w nieskończoności, tzn.

${\displaystyle U=V_{\mathrm {C} }(\infty )-V_{\mathrm {C} }(r_{0})=0-V_{\mathrm {C} }(r_{0})={\frac {e}{4\pi \epsilon _{0}r_{0}}}.}$

Wtedy w punktach dokładnego rezonansu otrzymujemy kwantowanie oporu bez żadnych stałych proporcjonalności podobnie jak w oryginalnym eksperymencie Klausa von Klitzinga jedynie z tą różnicą, że jest on proporcjonalny, a nie odwrotnie proporcjonalny do ${\displaystyle n,}$ tzn.

${\displaystyle R_{n}=U/I={\frac {h}{e^{2}}}n=n\;25812,807557\;\Omega .}$

Jest to także kwantowanie tego oporu zdefiniowanego tak samo dla oryginalnego modelu atomu Bohra, tzn. gdyby elektron klasyczny definiujący prąd jednoelektronowy poruszał się po skwantowanych orbitach kołowych pod prostopadłym do niego napięciem jądrowym względem nieskończoności kompensującym siłę odśrodkowa, tzn. tu mechaniczną siłę Lorentza. Stała von Klitzinga ${\displaystyle {h}/{e^{2}}=25812,807557\;\Omega }$ jest więc wartością tak zdefiniowanego oporu dla pierwszej orbity Bohra.

Zobacz też

• cykloatom

Bibliografia

• M. Kalinski, J.H. Eberly, Trojan wave packets: Mathieu theory and generation from circular states, Phys. Rev. A 53, s. 1715–1724 (1996).
• L. Sirko, P.M. Koch, The pendulum approximation for the main quantal resonance in periodically driven Hydrogen atoms, Appl. Phys. B 60, s. S195–S202 (1995).
• H. Klar, Periodic orbits in atomic hydrogen exposed to circularly polarised laser light, Z. Phys. D 11, s. 45–52 (1989).
• Z. Białynicka-Birula, Trojańskie paczki falowe, Postępy Fizyki 49, a. 164–170, 1998.
• H. Maeda, T.F. Gallagher, Nondispersing wave packets, Physical Review A 75, 033410-1-11 (2007).
• H. Maeda, J.H. Gurian, and T.F. Gallagher, Nondispersing Bohr Wave Packets, Phys. Rev. Lett. 102, 103001-1-4 (2009).
• C.R. Stroud, Jr., An astronomical solution to an old quantum problem, Physics 2, 19 (2009)
• K. Urbański, Elektron jak planetoida trojańska, „Rzeczpospolita”, 11.02.2010
• J.H. Eberly, L. Allen, Optical Resonance and Two-Level Atoms (Dover, 1987).
• G.A. Smith, Apparatus And Method For Long-term Storage Of Antimatter, US Patent #7709819, 2010
• M. Kalinski, Quantum Theory of a Hydrogen Atom in a Circularly Polarized Electromagnetic Field Near the Principal Resonance, PhD Thesis, University of Rochester 1997.
• B. Wyker, S. Ye, F.B. Dunning, S. Yoshida, C.O. Reinhold, and J. Burgdörfer, Creating and Transporting Trojan Wave Packets, Phys. Rev. Lett. 108, 043001 (2012).
• F. Aigner, Jupiter’s „Trojans” on an Atomic Scale, TU Wien News, 24.01.2012
• C. Cerjan, E. Lee, D. Farrelly, and T. Uzer, Coherent States in a Rydberg atom: Quantum mechanics, Phys. Rev. A 55, s. 2222–2231 (1997)
• Lambert M. Surhone, Miriam T. Timpledon, Susan F. Marseken, Trojan Wave Packet, Betascript Publishing 2010 ISBN 978-6130460662.

Linki zewnętrzne

• Ewolucja czasowa stanu koherentnego (symulator Java). web.ift.uib.no. [zarchiwizowane z tego adresu (2019-08-02)].
• Kwantowa natura paczek trojańskich w eksperymencie Aharonowa-Bohma (filmy)
• Gigantyczne podwójne paczki trojańskie z asteroid w Układzie Słonecznym – asteroidy trojańskie – symulacja. sajri.astronomy.cz. [zarchiwizowane z tego adresu (2010-06-22)].
• Paczka trojańska dla dowolnej wartości parametrów (symulator Java3D)
• Krótki wykład odkrywcy Paczek Trojańskich Matta Kalinskiego o ich teorii kwantowej jako stanów Starka-Zeemana i możliwych rozszerzeniach na atomy wieloelektronowe – film na youtube
• Zjawisko odwrotne – cykloatomy (Prezentacja PPT Roberta Wagnera) – przyspieszone przeciw intuicyjne relatywistyczne rozpływanie się w pierścień przypominającej stan podstawowy wąskiej gausowskiej paczki falowej w atomie wodoru w super-silnych polu magnetycznym i lasera (trudno je intuicyjnie zrozumieć ponieważ relatywistyczna dyspersja energii Diraca i Kleina-Gordona względem pędu przy dużych energiach staje się liniowa, tzn. charakterystyczna dla równania falowego fotonu które zawsze przewiduje dowolne rozwiązania o niezmiennym kształcie poruszającym się z prędkością światła, a na dodatek paczka jest w potencjale harmonicznym pola magnetycznego, czyli jest pochodna stanu koherentnego) (animacja)