Tensor algebras

Let ${\displaystyle {\mathcal {C}}}$ be the category of vector spaces ${\displaystyle K}$-Vect over a field ${\displaystyle K}$ and let ${\displaystyle {\mathcal {D}}}$ be the category of algebras ${\displaystyle K}$-Alg over ${\displaystyle K}$ (assumed to be unital and associative). Let

${\displaystyle U}$ : ${\displaystyle K}$-Alg → ${\displaystyle K}$-Vect

be the forgetful functor which assigns to each algebra its underlying vector space.

Given any vector space ${\displaystyle V}$ over ${\displaystyle K}$ we can construct the tensor algebra ${\displaystyle T(V)}$. The tensor algebra is characterized by the fact:

“Any linear map from ${\displaystyle V}$ to an algebra ${\displaystyle A}$ can be uniquely extended to an algebra homomorphism from ${\displaystyle T(V)}$ to ${\displaystyle A}$.”

This statement is an initial property of the tensor algebra since it expresses the fact that the pair ${\displaystyle (T(V),i)}$, where ${\displaystyle i:V\to U(T(V))}$ is the inclusion map, is a universal morphism from the vector space ${\displaystyle V}$ to the functor ${\displaystyle U}$.

Since this construction works for any vector space ${\displaystyle V}$, we conclude that ${\displaystyle T}$ is a functor from ${\displaystyle K}$-Vect to ${\displaystyle K}$-Alg. This means that ${\displaystyle T}$ is left adjoint to the forgetful functor ${\displaystyle U}$ (see the section below on relation to adjoint functors).

Products

A categorical product can be characterized by a universal construction. For concreteness, one may consider the Cartesian product in Set, the direct product in Grp, or the product topology in Top, where products exist.

Let ${\displaystyle X}$ and ${\displaystyle Y}$ be objects of a category ${\displaystyle {\mathcal {C}}}$ with finite products. The product of ${\displaystyle X}$ and ${\displaystyle Y}$ is an object ${\displaystyle X}$ × ${\displaystyle Y}$ together with two morphisms

${\displaystyle \pi _{1}}$ : ${\displaystyle X\times Y\to X}$

${\displaystyle \pi _{2}}$ : ${\displaystyle X\times Y\to Y}$

such that for any other object ${\displaystyle Z}$ of ${\displaystyle {\mathcal {C}}}$ and morphisms ${\displaystyle f:Z\to X}$ and ${\displaystyle g:Z\to Y}$ there exists a unique morphism ${\displaystyle h:Z\to X\times Y}$ such that ${\displaystyle f=\pi _{1}\circ h}$ and ${\displaystyle g=\pi _{2}\circ h}$.

To understand this characterization as a universal property, take the category ${\displaystyle {\mathcal {D}}}$ to be the product category ${\displaystyle {\mathcal {C}}\times {\mathcal {C}}}$ and define the diagonal functor

${\displaystyle \Delta$ :{\mathcal {C}}\to {\mathcal {C}}\times {\mathcal {C}}}

by ${\displaystyle \Delta (X)=(X,X)}$ and ${\displaystyle \Delta (f:X\to Y)=(f,f)}$. Then ${\displaystyle (X\times Y,(\pi _{1},\pi _{2}))}$ is a universal morphism from ${\displaystyle \Delta }$ to the object ${\displaystyle (X,Y)}$ of ${\displaystyle {\mathcal {C}}\times {\mathcal {C}}}$: if ${\displaystyle (f,g)}$ is any morphism from ${\displaystyle (Z,Z)}$ to ${\displaystyle (X,Y)}$, then it must equal a morphism ${\displaystyle \Delta (h:Z\to X\times Y)=(h,h)}$ from ${\displaystyle \Delta (Z)=(Z,Z)}$ to ${\displaystyle \Delta (X\times Y)=(X\times Y,X\times Y)}$ followed by ${\displaystyle (\pi _{1},\pi _{2})}$. As a commutative diagram:

Commutative diagram showing how products have a universal property.

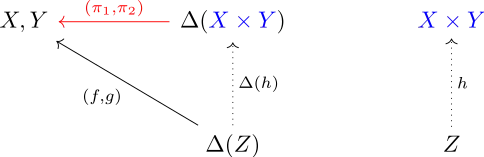
For the example of the Cartesian product in Set, the morphism ${\displaystyle (\pi _{1},\pi _{2})}$ comprises the two projections ${\displaystyle \pi _{1}(x,y)=x}$ and ${\displaystyle \pi _{2}(x,y)=y}$. Given any set ${\displaystyle Z}$ and functions ${\displaystyle f,g}$ the unique map such that the required diagram commutes is given by ${\displaystyle h=\langle x,y\rangle (z)=(f(z),g(z))}$.^[3]

Limits and colimits

Categorical products are a particular kind of limit in category theory. One can generalize the above example to arbitrary limits and colimits.

Let ${\displaystyle {\mathcal {J}}}$ and ${\displaystyle {\mathcal {C}}}$ be categories with ${\displaystyle {\mathcal {J}}}$ a small index category and let ${\displaystyle {\mathcal {C}}^{\mathcal {J}}}$ be the corresponding functor category. The diagonal functor

${\displaystyle \Delta$ :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}}

is the functor that maps each object ${\displaystyle N}$ in ${\displaystyle {\mathcal {C}}}$ to the constant functor ${\displaystyle \Delta (N):{\mathcal {J}}\to {\mathcal {C}}}$ (i.e. ${\displaystyle \Delta (N)(X)=N}$ for each ${\displaystyle X}$ in ${\displaystyle {\mathcal {J}}}$ and ${\displaystyle \Delta (N)(f)=1_{N}}$ for each ${\displaystyle f:X\to Y}$ in ${\displaystyle {\mathcal {J}}}$) and each morphism ${\displaystyle f:N\to M}$ in ${\displaystyle {\mathcal {C}}}$ to the natural transformation ${\displaystyle \Delta (f):\Delta (N)\to \Delta (M)}$ in ${\displaystyle {\mathcal {C}}^{\mathcal {J}}}$ defined as, for every object ${\displaystyle X}$ of ${\displaystyle {\mathcal {J}}}$, the component

$${\displaystyle \Delta (f)(X):\Delta (N)(X)\to \Delta (M)(X)=f:N\to M}$$

at ${\displaystyle X}$. In other words, the natural transformation is the one defined by having constant component ${\displaystyle f:N\to M}$ for every object of ${\displaystyle {\mathcal {J}}}$.

Given a functor ${\displaystyle F:{\mathcal {J}}\to {\mathcal {C}}}$ (thought of as an object in ${\displaystyle {\mathcal {C}}^{\mathcal {J}}}$), the limit of ${\displaystyle F}$, if it exists, is nothing but a universal morphism from ${\displaystyle \Delta }$ to ${\displaystyle F}$. Dually, the colimit of ${\displaystyle F}$ is a universal morphism from ${\displaystyle F}$ to ${\displaystyle \Delta }$.

Existence and uniqueness

Defining a quantity does not guarantee its existence. Given a functor ${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$ and an object ${\displaystyle X}$ of ${\displaystyle {\mathcal {D}}}$, there may or may not exist a universal morphism from ${\displaystyle X}$ to ${\displaystyle F}$. If, however, a universal morphism ${\displaystyle (A,u)}$ does exist, then it is essentially unique. Specifically, it is unique up to a unique isomorphism: if ${\displaystyle (A',u')}$ is another pair, then there exists a unique isomorphism ${\displaystyle k:A\to A'}$ such that ${\displaystyle u'=F(k)\circ u}$. This is easily seen by substituting ${\displaystyle (A,u')}$ in the definition of a universal morphism.

It is the pair ${\displaystyle (A,u)}$ which is essentially unique in this fashion. The object ${\displaystyle A}$ itself is only unique up to isomorphism. Indeed, if ${\displaystyle (A,u)}$ is a universal morphism and ${\displaystyle k:A\to A'}$ is any isomorphism then the pair ${\displaystyle (A',u')}$, where ${\displaystyle u'=F(k)\circ u}$ is also a universal morphism.

Equivalent formulations

The definition of a universal morphism can be rephrased in a variety of ways. Let ${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$ be a functor and let ${\displaystyle X}$ be an object of ${\displaystyle {\mathcal {D}}}$. Then the following statements are equivalent:

• ${\displaystyle (A,u)}$ is a universal morphism from ${\displaystyle X}$ to ${\displaystyle F}$
• ${\displaystyle (A,u)}$ is an initial object of the comma category ${\displaystyle (X\downarrow F)}$
• ${\displaystyle (A,F(\bullet )\circ u)}$ is a representation of ${\displaystyle {\text{Hom}}_{\mathcal {D}}(X,F(-))}$, where its components ${\displaystyle (F(\bullet )\circ u)_{B}:{\text{Hom}}_{\mathcal {C}}(A,B)\to {\text{Hom}}_{\mathcal {D}}(X,F(B))}$ are defined by

$${\displaystyle (F(\bullet )\circ u)_{B}(f:A\to B):X\to F(B)=F(f)\circ u:X\to F(B)}$$

for each object ${\displaystyle B}$ in ${\displaystyle {\mathcal {C}}.}$

The dual statements are also equivalent:

• ${\displaystyle (A,u)}$ is a universal morphism from ${\displaystyle F}$ to ${\displaystyle X}$
• ${\displaystyle (A,u)}$ is a terminal object of the comma category ${\displaystyle (F\downarrow X)}$
• ${\displaystyle (A,u\circ F(\bullet ))}$ is a representation of ${\displaystyle {\text{Hom}}_{\mathcal {D}}(F(-),X)}$, where its components ${\displaystyle (u\circ F(\bullet ))_{B}:{\text{Hom}}_{\mathcal {C}}(B,A)\to {\text{Hom}}_{\mathcal {D}}(F(B),X)}$ are defined by

$${\displaystyle (u\circ F(\bullet ))_{B}(f:B\to A):F(B)\to X=u\circ F(f):F(B)\to X}$$

for each object ${\displaystyle B}$ in ${\displaystyle {\mathcal {C}}.}$

Relation to adjoint functors

Suppose ${\displaystyle (A_{1},u_{1})}$ is a universal morphism from ${\displaystyle X_{1}}$ to ${\displaystyle F}$ and ${\displaystyle (A_{2},u_{2})}$ is a universal morphism from ${\displaystyle X_{2}}$ to ${\displaystyle F}$. By the universal property of universal morphisms, given any morphism ${\displaystyle h:X_{1}\to X_{2}}$ there exists a unique morphism ${\displaystyle g:A_{1}\to A_{2}}$ such that the following diagram commutes:

Universal morphisms can behave like a natural transformation between functors under suitable conditions.

If every object ${\displaystyle X_{i}}$ of ${\displaystyle {\mathcal {D}}}$ admits a universal morphism to ${\displaystyle F}$, then the assignment ${\displaystyle X_{i}\mapsto A_{i}}$ and ${\displaystyle h\mapsto g}$ defines a functor ${\displaystyle G:{\mathcal {D}}\to {\mathcal {C}}}$. The maps ${\displaystyle u_{i}}$ then define a natural transformation from ${\displaystyle 1_{\mathcal {D}}}$ (the identity functor on ${\displaystyle {\mathcal {D}}}$) to ${\displaystyle F\circ G}$. The functors ${\displaystyle (F,G)}$ are then a pair of adjoint functors, with ${\displaystyle G}$ left-adjoint to ${\displaystyle F}$ and ${\displaystyle F}$ right-adjoint to ${\displaystyle G}$.

Similar statements apply to the dual situation of terminal morphisms from ${\displaystyle F}$. If such morphisms exist for every ${\displaystyle X}$ in ${\displaystyle {\mathcal {C}}}$ one obtains a functor ${\displaystyle G:{\mathcal {C}}\to {\mathcal {D}}}$ which is right-adjoint to ${\displaystyle F}$ (so ${\displaystyle F}$ is left-adjoint to ${\displaystyle G}$).

Indeed, all pairs of adjoint functors arise from universal constructions in this manner. Let ${\displaystyle F}$ and ${\displaystyle G}$ be a pair of adjoint functors with unit ${\displaystyle \eta }$ and co-unit ${\displaystyle \epsilon }$ (see the article on adjoint functors for the definitions). Then we have a universal morphism for each object in ${\displaystyle {\mathcal {C}}}$ and ${\displaystyle {\mathcal {D}}}$:

• For each object ${\displaystyle X}$ in ${\displaystyle {\mathcal {C}}}$, ${\displaystyle (F(X),\eta _{X})}$ is a universal morphism from ${\displaystyle X}$ to ${\displaystyle G}$. That is, for all ${\displaystyle f:X\to G(Y)}$ there exists a unique ${\displaystyle g:F(X)\to Y}$ for which the following diagrams commute.
• For each object ${\displaystyle Y}$ in ${\displaystyle {\mathcal {D}}}$, ${\displaystyle (G(Y),\epsilon _{Y})}$ is a universal morphism from ${\displaystyle F}$ to ${\displaystyle Y}$. That is, for all ${\displaystyle g:F(X)\to Y}$ there exists a unique ${\displaystyle f:X\to G(Y)}$ for which the following diagrams commute.

The unit and counit of an adjunction, which are natural transformations between functors, are an important example of universal morphisms.

Universal constructions are more general than adjoint functor pairs: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of ${\displaystyle {\mathcal {C}}}$ (equivalently, every object of ${\displaystyle {\mathcal {D}}}$).