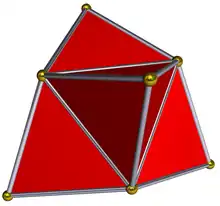
| Triakis tetrahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kT |
| Face type | V3.6.6 isosceles triangle |
| Faces | 12 |
| Edges | 18 |
| Vertices | 8 |
| Vertices by type | 4{3}+4{6} |
| Symmetry group | Td, A3, [3,3], (*332) |
| Rotation group | T, [3,3]+, (332) |
| Dihedral angle | 129°31′16″ arccos(−7/11) |
| Properties | convex, face-transitive |
 Truncated tetrahedron (dual polyhedron) |
 Net |

In geometry, a triakis tetrahedron (or kistetrahedron[1]) is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron.
The triakis tetrahedron can be seen as a tetrahedron with a triangular pyramid added to each face; that is, it is the Kleetope of the tetrahedron. It is very similar to the net for the 5-cell, as the net for a tetrahedron is a triangle with other triangles added to each edge, the net for the 5-cell a tetrahedron with pyramids attached to each face. This interpretation is expressed in the name.
The length of the shorter edges is 3/5 that of the longer edges.[2] If the triakis tetrahedron has shorter edge length 1, it has area 5/3√11 and volume 25/36√2.
Cartesian coordinates
Cartesian coordinates for the 8 vertices of a triakis tetrahedron centered at the origin, are the points (±5/3, ±5/3, ±5/3) with an even number of minus signs, along with the points (±1, ±1, ±1) with an odd number of minus signs:
- (5/3, 5/3, 5/3), (5/3, −5/3, −5/3), (−5/3, 5/3, −5/3), (−5/3, −5/3, 5/3)
- (−1, 1, 1), (1, −1, 1), (1, 1, −1), (−1, −1, −1)
The length of the shorter edges of this triakis tetrahedron equals 2√2. The faces are isosceles triangles with one obtuse and two acute angles. The obtuse angle equals arccos(–7/18) ≈ 112.88538047616° and the acute ones equal arccos(5/6) ≈ 33.55730976192°.
Tetartoid symmetry
The triakis tetrahedron can be made as a degenerate limit of a tetartoid:
 |
 |
 |
 |
 |
 |
 |
 |
Orthogonal projections
| Orthogonal projections (graphs) | ||||
|---|---|---|---|---|
| Centered by | Short edge | Face | Vertex | Long edge |
| Triakis tetrahedron |
 |
 |
 |
 |
| (Dual) Truncated tetrahedron |
 |
 |
 |
 |
| Projective symmetry |
[1] | [3] | [4] | |
| Orthogonal projections (solids) | ||||
|---|---|---|---|---|
| Triakis tetrahedron |
 |
 |
 |
 |
| Dual compound |
 |
 |
 |
 |
| (Dual) Truncated tetrahedron |
 |
 |
 |
 |
| Projective symmetry |
[1] | [2] | [3] | |
Variations
A triakis tetrahedron with equilateral triangle faces represents a net of the four-dimensional regular polytope known as the 5-cell.
If the triangles are right-angled isosceles, the faces will be coplanar and form a cubic volume. This can be seen by adding the 6 edges of tetrahedron inside of a cube.
In modular origami, this is the result to connecting six Sonobe modules to form a triakis tetrahedron.
Stellations
This chiral figure is one of thirteen stellations allowed by Miller's rules.
Related polyhedra

The triakis tetrahedron is a part of a sequence of polyhedra and tilings, extending into the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.
| *n32 symmetry mutation of truncated tilings: t{n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
| Truncated figures |
 |
 |
 |
 |
 |
 |
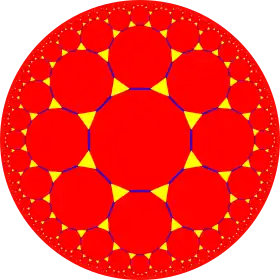 |
 |
 |
 |
 |
| Symbol | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{∞,3} | t{12i,3} | t{9i,3} | t{6i,3} |
| Triakis figures |
 |
 |
 |
 |
 |
 |
 |
 |
|||
| Config. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
| Family of uniform tetrahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [3,3], (*332) | [3,3]+, (332) | ||||||
 |
 |
 |
 |
||||
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
See also
References
- ↑ Conway, Symmetries of things, p.284
- ↑ "Triakis Tetrahedron - Geometry Calculator".
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, Page 14, Triakistetrahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis tetrahedron )
External links