Tresca yield surface

The Tresca yield criterion is taken to be the work of Henri Tresca.^[11] It is also known as the maximum shear stress theory (MSST) and the Tresca–Guest^[12] (TG) criterion. In terms of the principal stresses the Tresca criterion is expressed as

${\displaystyle {\tfrac {1}{2}}{\max(|\sigma _{1}-\sigma _{2}|,|\sigma _{2}-\sigma _{3}|,|\sigma _{3}-\sigma _{1}|)=S_{sy}={\tfrac {1}{2}}S_{y}}\!}$

Where ${\displaystyle S_{sy}}$ is the yield strength in shear, and ${\displaystyle S_{y}}$ is the tensile yield strength.

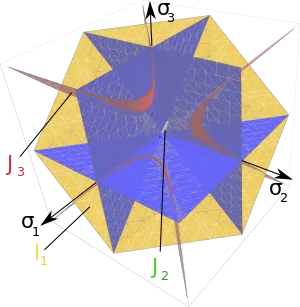
Figure 1 shows the Tresca–Guest yield surface in the three-dimensional space of principal stresses. It is a prism of six sides and having infinite length. This means that the material remains elastic when all three principal stresses are roughly equivalent (a hydrostatic pressure), no matter how much it is compressed or stretched. However, when one of the principal stresses becomes smaller (or larger) than the others the material is subject to shearing. In such situations, if the shear stress reaches the yield limit then the material enters the plastic domain. Figure 2 shows the Tresca–Guest yield surface in two-dimensional stress space, it is a cross section of the prism along the ${\displaystyle \sigma _{1},\sigma _{2}}$ plane.

Figure 1: View of Tresca–Guest yield surface in 3D space of principal stresses

Figure 2: Tresca–Guest yield surface in 2D space (${\displaystyle \sigma _{1},\sigma _{2}}$)

von Mises yield surface

The von Mises yield criterion is expressed in the principal stresses as

${\displaystyle {(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}=2{S_{y}}^{2}}\!}$

where ${\displaystyle S_{y}}$ is the yield strength in uniaxial tension.

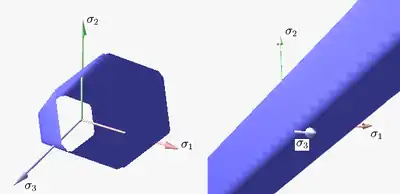
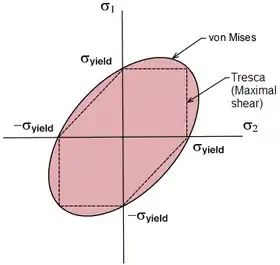
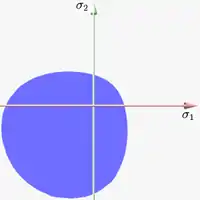
Figure 3 shows the von Mises yield surface in the three-dimensional space of principal stresses. It is a circular cylinder of infinite length with its axis inclined at equal angles to the three principal stresses. Figure 4 shows the von Mises yield surface in two-dimensional space compared with Tresca–Guest criterion. A cross section of the von Mises cylinder on the plane of ${\displaystyle \sigma _{1},\sigma _{2}}$ produces the elliptical shape of the yield surface.

Figure 3: View of Huber–Mises–Hencky yield surface in 3D space of principal stresses

Figure 4: Comparison of Tresca–Guest and Huber–Mises–Hencky criteria in 2D space (${\displaystyle \sigma _{1},\sigma _{2}}$)

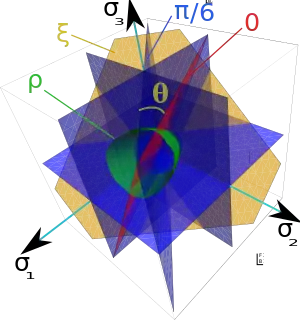
Burzyński-Yagn criterion

This criterion^[13][14]

${\displaystyle 3I_{2}'={\frac {\sigma _{\mathrm {eq} }-\gamma _{1}I_{1}}{1-\gamma _{1}}}{\frac {\sigma _{\mathrm {eq} }-\gamma _{2}I_{1}}{1-\gamma _{2}}}}$

represents the general equation of a second order surface of revolution about the hydrostatic axis. Some special case are:^[15]

• cylinder ${\displaystyle \gamma _{1}=\gamma _{2}=0}$ (Maxwell (1865), Huber (1904), von Mises (1913), Hencky (1924)),
• cone ${\displaystyle \gamma _{1}=\gamma _{2}\in ]0,1[}$ (Botkin (1940), Drucker-Prager (1952), Mirolyubov (1953)),
• paraboloid ${\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}=0}$ (Burzyński (1928), Balandin (1937), Torre (1947)),
• ellipsoid centered of symmetry plane ${\displaystyle I_{1}=0}$, ${\displaystyle \gamma _{1}=-\gamma _{2}\in ]0,1[}$ (Beltrami (1885)),
• ellipsoid centered of symmetry plane ${\displaystyle I_{1}={\frac {1}{2}}\,{\bigg (}{\frac {1}{\gamma _{1}}}+{\frac {1}{\gamma _{2}}}{\bigg )}}$ with ${\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}<0}$ (Schleicher (1926)),
• hyperboloid of two sheets ${\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}\in ]0,\gamma _{1}[}$ (Burzynski (1928), Yagn (1931)),
• hyperboloid of one sheet centered of symmetry plane ${\displaystyle I_{1}=0}$, ${\displaystyle \gamma _{1}=-\gamma _{2}=a\,i}$, ${\displaystyle i={\sqrt {-1}}}$ (Kuhn (1980))
• hyperboloid of one sheet ${\displaystyle \gamma _{1,2}=b\pm a\,i}$, ${\displaystyle i={\sqrt {-1}}}$ (Filonenko-Boroditsch (1960), Gol’denblat-Kopnov (1968), Filin (1975)).

The relations compression-tension and torsion-tension can be computed to

${\displaystyle {\frac {\sigma _{-}}{\sigma _{+}}}={\frac {1}{1-\gamma _{1}-\gamma _{2}}},\qquad {\bigg (}{\sqrt {3}}\,{\frac {\tau _{*}}{\sigma _{+}}}{\bigg )}^{2}={\frac {1}{(1-\gamma _{1})(1-\gamma _{2})}}}$

The Poisson's ratios at tension and compression are obtained using

${\displaystyle \nu _{+}^{\mathrm {in} }={\frac {-1+2(\gamma _{1}+\gamma _{2})-3\gamma _{1}\gamma _{2}}{-2+\gamma _{1}+\gamma _{2}}}}$

${\displaystyle \nu _{-}^{\mathrm {in} }=-{\frac {-1+\gamma _{1}^{2}+\gamma _{2}^{2}-\gamma _{1}\,\gamma _{2}}{(-2+\gamma _{1}+\gamma _{2})\,(-1+\gamma _{1}+\gamma _{2})}}}$

For ductile materials the restriction

${\displaystyle \nu _{+}^{\mathrm {in} }\in {\bigg [}\,0.48,\,{\frac {1}{2}}\,{\bigg ]}}$

is important. The application of rotationally symmetric criteria for brittle failure with

${\displaystyle \nu _{+}^{\mathrm {in} }\in ]-1,~\nu _{+}^{\mathrm {el} }\,]}$

has not been studied sufficiently.^[16]

The Burzyński-Yagn criterion is well suited for academic purposes. For practical applications, the third invariant of the deviator in the odd and even power should be introduced in the equation, e.g.:^[17]

${\displaystyle 3I_{2}'{\frac {1+c_{3}\cos 3\theta +c_{6}\cos ^{2}3\theta }{1+c_{3}+c_{6}}}={\frac {\sigma _{\mathrm {eq} }-\gamma _{1}I_{1}}{1-\gamma _{1}}}{\frac {\sigma _{\mathrm {eq} }-\gamma _{2}I_{1}}{1-\gamma _{2}}}}$

Huber criterion

The Huber criterion consists of the Beltrami ellipsoid and a scaled von Mises cylinder in the principal stress space,^{[18][19][20][21]} see also^[22][23]

${\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll}\displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\,I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }+\gamma _{1}\,I_{1}}{1+\gamma _{1}}},&I_{1}>0\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} }}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }}{1+\gamma _{1}}},&I_{1}\leq 0\end{array}}\right.}$

with ${\displaystyle \gamma _{1}\in [0,1[}$. The transition between the surfaces in the cross section ${\displaystyle I_{1}=0}$ is continuously differentiable. The criterion represents the "classical view" with respect to inelastic material behavior:

• pressure-sensitive material behavior for ${\displaystyle I_{1}>0}$ with ${\displaystyle \nu _{+}^{\mathrm {in} }\in \left]-1,\,1/2\right]}$ and
• pressure-insensitive material behavior for ${\displaystyle I_{1}<0}$ with ${\displaystyle \nu _{-}^{\mathrm {in} }=1/2}$

The Huber criterion can be used as a yield surface with an empirical restriction for Poisson's ratio at tension ${\displaystyle \nu _{+}^{\mathrm {in} }\in [0.48,1/2]}$, which leads to ${\displaystyle \gamma _{1}\in [0,0.1155]}$.

Huber criterion with ${\displaystyle \gamma _{1}=1/{\sqrt {3}}}$ and modified Huber criterion with ${\displaystyle \gamma _{1}=(1+{\sqrt {5}})/6}$ and ${\displaystyle \gamma _{2}=(1-{\sqrt {5}})/6}$ in the Burzyński-plane: setting according the normal stress hypothesis (${\displaystyle \nu _{+}^{\mathrm {in} }=0}$). The von Mises criterion (${\displaystyle \nu _{-}^{\mathrm {in} }=\nu _{+}^{\mathrm {in} }=1/2}$) is shown for comparison.

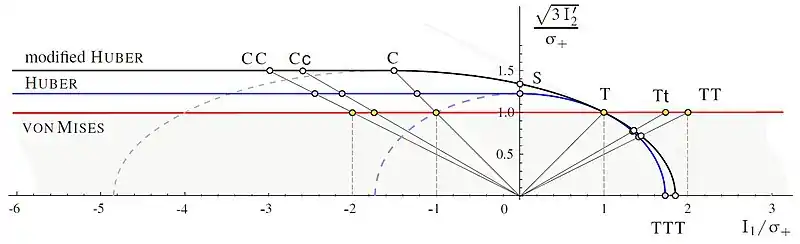
The modified Huber criterion,^[24][23] see also,^[25] cf. ^[26]

${\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll}\displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\,I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }-\gamma _{2}\,I_{1}}{1-\gamma _{2}}},&I_{1}>-d\,\sigma _{\mathrm {+} }\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} }^{2}}{(1-\gamma _{1}-\gamma _{2})^{2}}},&I_{1}\leq -d\,\sigma _{\mathrm {+} }\end{array}}\right.}$

consists of the Schleicher ellipsoid with the restriction of Poisson's ratio at compression

${\displaystyle \nu _{-}^{\mathrm {in} }=-{\frac {-1+\gamma _{1}^{2}+\gamma _{2}^{2}-\gamma _{1}\,\gamma _{2}}{(-2+\gamma _{1}+\gamma _{2})\,(-1+\gamma _{1}+\gamma _{2})}}={\frac {1}{2}}}$

and a cylinder with the ${\displaystyle C^{1}}$-transition in the cross section ${\displaystyle I_{1}=-d\,\sigma _{\mathrm {+} }}$. The second setting for the parameters ${\displaystyle \gamma _{1}\in [0,1[}$ and ${\displaystyle \gamma _{2}<0}$ follows with the compression / tension relation

${\displaystyle d={\frac {\sigma _{-}}{\sigma _{+}}}={\frac {1}{1-\gamma _{1}-\gamma _{2}}}\geq 1}$

The modified Huber criterion can be better fitted to the measured data as the Huber criterion. For setting ${\displaystyle \nu _{+}^{\mathrm {in} }=0.48}$ it follows ${\displaystyle \gamma _{1}=0.0880}$ and ${\displaystyle \gamma _{2}=-0.0747}$.

The Huber criterion and the modified Huber criterion should be preferred to the von Mises criterion since one obtains safer results in the region ${\displaystyle I_{1}>\sigma _{\mathrm {+} }}$. For practical applications the third invariant of the deviator ${\displaystyle I_{3}'}$ should be considered in these criteria.^[23]

Mohr–Coulomb yield surface

The Mohr–Coulomb yield (failure) criterion is similar to the Tresca criterion, with additional provisions for materials with different tensile and compressive yield strengths. This model is often used to model concrete, soil or granular materials. The Mohr–Coulomb yield criterion may be expressed as:

${\displaystyle {\frac {m+1}{2}}\max {\Big (}|\sigma _{1}-\sigma _{2}|+K(\sigma _{1}+\sigma _{2})~,~~|\sigma _{1}-\sigma _{3}|+K(\sigma _{1}+\sigma _{3})~,~~|\sigma _{2}-\sigma _{3}|+K(\sigma _{2}+\sigma _{3}){\Big )}=S_{yc}}$

where

${\displaystyle m={\frac {S_{yc}}{S_{yt}}};K={\frac {m-1}{m+1}}}$

and the parameters ${\displaystyle S_{yc}}$ and ${\displaystyle S_{yt}}$ are the yield (failure) stresses of the material in uniaxial compression and tension, respectively. The formula reduces to the Tresca criterion if ${\displaystyle S_{yc}=S_{yt}}$.

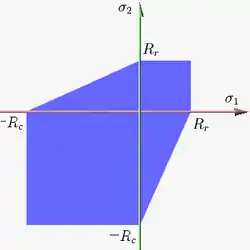
Figure 5 shows Mohr–Coulomb yield surface in the three-dimensional space of principal stresses. It is a conical prism and ${\displaystyle K}$ determines the inclination angle of conical surface. Figure 6 shows Mohr–Coulomb yield surface in two-dimensional stress space. In Figure 6 ${\displaystyle R_{r}}$ and ${\displaystyle R_{c}}$ is used for ${\displaystyle S_{yt}}$ and ${\displaystyle S_{yc}}$, respectively, in the formula. It is a cross section of this conical prism on the plane of ${\displaystyle \sigma _{1},\sigma _{2}}$. In Figure 6 Rr and Rc are used for Syc and Syt, respectively, in the formula.

Figure 5: View of Mohr–Coulomb yield surface in 3D space of principal stresses

Figure 6: Mohr–Coulomb yield surface in 2D space (${\displaystyle \sigma _{1},\sigma _{2}}$)

Drucker–Prager yield surface

The Drucker–Prager yield criterion is similar to the von Mises yield criterion, with provisions for handling materials with differing tensile and compressive yield strengths. This criterion is most often used for concrete where both normal and shear stresses can determine failure. The Drucker–Prager yield criterion may be expressed as

${\displaystyle {\bigg (}{\frac {m-1}{2}}{\bigg )}(\sigma _{1}+\sigma _{2}+\sigma _{3})+{\bigg (}{\frac {m+1}{2}}{\bigg )}{\sqrt {\frac {(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}}{2}}}=S_{yc}}$

where

${\displaystyle m={\frac {S_{yc}}{S_{yt}}}}$

and ${\displaystyle S_{yc}}$, ${\displaystyle S_{yt}}$ are the uniaxial yield stresses in compression and tension respectively. The formula reduces to the von Mises equation if ${\displaystyle S_{yc}=S_{yt}}$.

Figure 7 shows Drucker–Prager yield surface in the three-dimensional space of principal stresses. It is a regular cone. Figure 8 shows Drucker–Prager yield surface in two-dimensional space. The elliptical elastic domain is a cross section of the cone on the plane of ${\displaystyle \sigma _{1},\sigma _{2}}$; it can be chosen to intersect the Mohr–Coulomb yield surface in different number of vertices. One choice is to intersect the Mohr–Coulomb yield surface at three vertices on either side of the ${\displaystyle \sigma _{1}=-\sigma _{2}}$ line, but usually selected by convention to be those in the compression regime.^[27] Another choice is to intersect the Mohr–Coulomb yield surface at four vertices on both axes (uniaxial fit) or at two vertices on the diagonal ${\displaystyle \sigma _{1}=\sigma _{2}}$ (biaxial fit).^[28] The Drucker-Prager yield criterion is also commonly expressed in terms of the material cohesion and friction angle.

Figure 7: View of Drucker–Prager yield surface in 3D space of principal stresses

Figure 8: View of Drucker–Prager yield surface in 2D space of principal stresses

Bresler–Pister yield surface

The Bresler–Pister yield criterion is an extension of the Drucker Prager yield criterion that uses three parameters, and has additional terms for materials that yield under hydrostatic compression. In terms of the principal stresses, this yield criterion may be expressed as

${\displaystyle S_{yc}={\tfrac {1}{\sqrt {2}}}\left[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}\right]^{1/2}-c_{0}-c_{1}~(\sigma _{1}+\sigma _{2}+\sigma _{3})-c_{2}~(\sigma _{1}+\sigma _{2}+\sigma _{3})^{2}}$

where ${\displaystyle c_{0},c_{1},c_{2}}$ are material constants. The additional parameter ${\displaystyle c_{2}}$ gives the yield surface an ellipsoidal cross section when viewed from a direction perpendicular to its axis. If ${\displaystyle \sigma _{c}}$ is the yield stress in uniaxial compression, ${\displaystyle \sigma _{t}}$ is the yield stress in uniaxial tension, and ${\displaystyle \sigma _{b}}$ is the yield stress in biaxial compression, the parameters can be expressed as

${\displaystyle {\begin{aligned}c_{1}=&\left({\cfrac {\sigma _{t}-\sigma _{c}}{(\sigma _{t}+\sigma _{c})}}\right)\left({\cfrac {4\sigma _{b}^{2}-\sigma _{b}(\sigma _{c}+\sigma _{t})+\sigma _{c}\sigma _{t}}{4\sigma _{b}^{2}+2\sigma _{b}(\sigma _{t}-\sigma _{c})-\sigma _{c}\sigma _{t}}}\right)\\c_{2}=&\left({\cfrac {1}{(\sigma _{t}+\sigma _{c})}}\right)\left({\cfrac {\sigma _{b}(3\sigma _{t}-\sigma _{c})-2\sigma _{c}\sigma _{t}}{4\sigma _{b}^{2}+2\sigma _{b}(\sigma _{t}-\sigma _{c})-\sigma _{c}\sigma _{t}}}\right)\\c_{0}=&c_{1}\sigma _{c}-c_{2}\sigma _{c}^{2}\end{aligned}}}$

Figure 9: View of Bresler–Pister yield surface in 3D space of principal stresses

Figure 10: Bresler–Pister yield surface in 2D space (${\displaystyle \sigma _{1},\sigma _{2}}$)

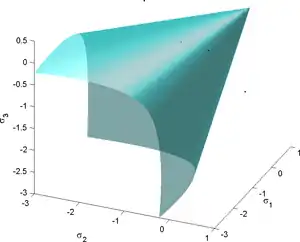
Willam–Warnke yield surface

The Willam–Warnke yield criterion is a three-parameter smoothed version of the Mohr–Coulomb yield criterion that has similarities in form to the Drucker–Prager and Bresler–Pister yield criteria.

The yield criterion has the functional form

${\displaystyle f(I_{1},J_{2},J_{3})=0~.}$

However, it is more commonly expressed in Haigh–Westergaard coordinates as

${\displaystyle f(\xi ,\rho ,\theta )=0~.}$

The cross-section of the surface when viewed along its axis is a smoothed triangle (unlike Mohr–Coulomb). The Willam–Warnke yield surface is convex and has unique and well defined first and second derivatives on every point of its surface. Therefore, the Willam–Warnke model is computationally robust and has been used for a variety of cohesive-frictional materials.

Figure 11: View of Willam–Warnke yield surface in 3D space of principal stresses

Figure 12: Willam–Warnke yield surface in the ${\displaystyle \pi }$-plane

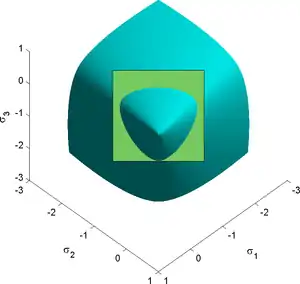
Podgórski and Rosendahl trigonometric yield surfaces

Normalized with respect to the uniaxial tensile stress ${\displaystyle \sigma _{\mathrm {eq} }=\sigma _{+}}$, the Podgórski criterion ^[29] as function of the stress angle ${\displaystyle \theta }$ reads

${\displaystyle \sigma _{\mathrm {eq} }={\sqrt {3\,I_{2}'}}\,{\frac {\Omega _{3}(\theta ,\beta _{3},\chi _{3})}{\Omega _{3}(0,\beta _{3},\chi _{3})}},}$

with the shape function of trigonal symmetry in the ${\displaystyle \pi }$-plane

${\displaystyle \Omega _{3}(\theta ,\beta _{3},\chi _{3})=\cos \left[\displaystyle {\frac {1}{3}}\left(\pi \beta _{3}-\arccos[\,\sin(\chi _{3}\,{\frac {\pi }{2}})\,\!\cos 3\,\theta \,]\right)\right],\qquad \beta _{3}\in [0,\,1],\quad \chi _{3}\in [-1,\,1].}$

It contains the criteria of von Mises (circle in the ${\displaystyle \pi }$-plane, ${\displaystyle \beta _{3}=[0,\,1]}$, ${\displaystyle \chi _{3}=0}$), Tresca (regular hexagon, ${\displaystyle \beta _{3}=1/2}$, ${\displaystyle \chi _{3}=\{1,-1\}}$), Mariotte (regular triangle, ${\displaystyle \beta _{3}=\{0,1\}}$, ${\displaystyle \chi _{3}=\{1,-1\}}$), Ivlev ^[30] (regular triangle, ${\displaystyle \beta _{3}=\{1,0\}}$, ${\displaystyle \chi _{3}=\{1,-1\}}$) and also the cubic criterion of Sayir ^[31] (the Ottosen criterion ^[32]) with ${\displaystyle \beta _{3}=\{0,1\}}$ and the isotoxal (equilateral) hexagons of the Capurso criterion^[30][31][33] with ${\displaystyle \chi _{3}=\{1,-1\}}$. The von Mises - Tresca transition ^[34] follows with ${\displaystyle \beta _{3}=1/2}$, ${\displaystyle \chi _{3}=[0,1]}$. The isogonal (equiangular) hexagons of the Haythornthwaite criterion ^[23][35][36] containing the Schmidt-Ishlinsky criterion (regular hexagon) cannot be described with the Podgórski ctiterion.

The Rosendahl criterion ^[37][38] reads

${\displaystyle \sigma _{\mathrm {eq} }={\sqrt {3\,I_{2}'}}\,{\frac {\Omega _{6}(\theta ,\beta _{6},\chi _{6})}{\Omega _{6}(0,\beta _{6},\chi _{6})}},}$

with the shape function of hexagonal symmetry in the ${\displaystyle \pi }$-plane

${\displaystyle \Omega _{6}(\theta ,\beta _{6},\chi _{6})=\cos \left[\displaystyle {\frac {1}{6}}\left(\pi \beta _{6}-\arccos[\,\sin(\chi _{6}\,{\frac {\pi }{2}})\,\!\cos 6\,\theta \,]\right)\right],\qquad \beta _{6}\in [0,\,1],\quad \chi _{6}\in [-1,\,1].}$

It contains the criteria of von Mises (circle, ${\displaystyle \beta _{6}=[0,\,1]}$, ${\displaystyle \chi _{6}=0}$), Tresca (regular hexagon, ${\displaystyle \beta _{6}=\{1,0\}}$, ${\displaystyle \chi _{6}=\{1,-1\}}$), Schmidt—Ishlinsky (regular hexagon, ${\displaystyle \beta _{6}=\{0,1\}}$, ${\displaystyle \chi _{6}=\{1,-1\}}$), Sokolovsky (regular dodecagon, ${\displaystyle \beta _{6}=1/2}$, ${\displaystyle \chi _{6}=\{1,-1\}}$), and also the bicubic criterion ^{[23][37][39][40]} with ${\displaystyle \beta _{6}=0}$ or equally with ${\displaystyle \beta _{6}=1}$ and the isotoxal dodecagons of the unified yield criterion of Yu ^[41] with ${\displaystyle \chi _{6}=\{1,-1\}}$. The isogonal dodecagons of the multiplicative ansatz criterion of hexagonal symmetry ^[23] containing the Ishlinsky-Ivlev criterion (regular dodecagon) cannot be described by the Rosendahl criterion.

The criteria of Podgórski and Rosendahl describe single surfaces in principal stress space without any additional outer contours and plane intersections. Note that in order to avoid numerical issues the real part function ${\displaystyle Re}$ can be introduced to the shape function: ${\displaystyle Re(\Omega _{3})}$ and ${\displaystyle Re(\Omega _{6})}$. The generalization in the form ${\displaystyle \Omega _{3n}}$^[37] is relevant for theoretical investigations.

A pressure-sensitive extension of the criteria can be obtained with the linear ${\displaystyle I_{1}}$-substitution ^[23]

${\displaystyle \sigma _{\mathrm {eq} }\rightarrow {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\,I_{1}}{1-\gamma _{1}}}\qquad {\mbox{with}}\qquad \gamma _{1}\in [0,\,1[,}$

which is sufficient for many applications, e.g. metals, cast iron, alloys, concrete, unreinforced polymers, etc.

Basic cross sections described by a circle and regular polygons of trigonal or hexagonal symmetries in the ${\displaystyle \pi }$-plane.

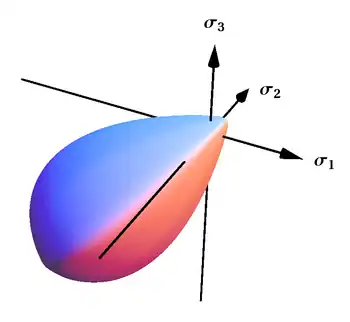
Bigoni–Piccolroaz yield surface

The Bigoni–Piccolroaz yield criterion^[42][43] is a seven-parameter surface defined by

${\displaystyle f(p,q,\theta )=F(p)+{\frac {q}{g(\theta )}}=0,}$

where ${\displaystyle F(p)}$ is the "meridian" function

${\displaystyle F(p)=\left\{{\begin{array}{ll}-Mp_{c}{\sqrt {(\phi -\phi ^{m})[2(1-\alpha )\phi +\alpha ]}},&\phi \in [0,1],\\+\infty ,&\phi \notin [0,1],\end{array}}\right.}$

${\displaystyle \phi ={\frac {p+c}{p_{c}+c}},}$

describing the pressure-sensitivity and ${\displaystyle g(\theta )}$ is the "deviatoric" function ^[44]

${\displaystyle g(\theta )={\frac {1}{\cos[\beta {\frac {\pi }{6}}-{\frac {1}{3}}\cos ^{-1}(\gamma \cos 3\theta )]}},}$

describing the Lode-dependence of yielding. The seven, non-negative material parameters:

${\displaystyle \underbrace {M>0,~p_{c}>0,~c\geq 0,~0<\alpha <2,~m>1} _{{\mbox{defining}}~\displaystyle {F(p)}},~~~\underbrace {0\leq \beta \leq 2,~0\leq \gamma <1} _{{\mbox{defining}}~\displaystyle {g(\theta )}},}$

define the shape of the meridian and deviatoric sections.

This criterion represents a smooth and convex surface, which is closed both in hydrostatic tension and compression and has a drop-like shape, particularly suited to describe frictional and granular materials. This criterion has also been generalized to the case of surfaces with corners.^[45]

In 3D space of principal stresses

In the ${\displaystyle \pi }$-plane

Bigoni-Piccolroaz yield surface

Cosine Ansatz (Altenbach-Bolchoun-Kolupaev)

For the formulation of the strength criteria the stress angle

${\displaystyle \cos 3\theta ={\frac {3{\sqrt {3}}}{2}}{\frac {I_{3}'}{I_{2}'^{\frac {3}{2}}}}}$

can be used.

The following criterion of isotropic material behavior

${\displaystyle (3I_{2}')^{3}{\frac {1+c_{3}\cos 3\theta +c_{6}\cos ^{2}3\theta }{1+c_{3}+c_{6}}}=\displaystyle \left({\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\,I_{1}}{1-\gamma _{1}}}\right)^{6-l-m}\,\left({\frac {\sigma _{\mathrm {eq} }-\gamma _{2}\,I_{1}}{1-\gamma _{2}}}\right)^{l}\,\sigma _{\mathrm {eq} }^{m}}$

contains a number of other well-known less general criteria, provided suitable parameter values are chosen.

Parameters ${\displaystyle c_{3}}$ and ${\displaystyle c_{6}}$ describe the geometry of the surface in the ${\displaystyle \pi }$-plane. They are subject to the constraints

${\displaystyle c_{6}={\frac {1}{4}}(2+c_{3}),\qquad c_{6}={\frac {1}{4}}(2-c_{3}),\qquad c_{6}\geq {\frac {5}{12}}\,c_{3}^{2}-{\frac {1}{3}},}$

which follow from the convexity condition. A more precise formulation of the third constraints is proposed in.^[46][47]

Parameters ${\displaystyle \gamma _{1}\in [0,\,1[}$ and ${\displaystyle \gamma _{2}}$ describe the position of the intersection points of the yield surface with hydrostatic axis (space diagonal in the principal stress space). These intersections points are called hydrostatic nodes. In the case of materials which do not fail at hydrostatic pressure (steel, brass, etc.) one gets ${\displaystyle \gamma _{2}\in [0,\,\gamma _{1}[}$. Otherwise for materials which fail at hydrostatic pressure (hard foams, ceramics, sintered materials, etc.) it follows ${\displaystyle \gamma _{2}<0}$.

The integer powers ${\displaystyle l\geq 0}$ and ${\displaystyle m\geq 0}$, ${\displaystyle l+m<6}$ describe the curvature of the meridian. The meridian with ${\displaystyle l=m=0}$ is a straight line and with ${\displaystyle l=0}$ – a parabola.

Barlat's Yield Surface

For the anisotropic materials, depending on the direction of the applied process (e.g., rolling) the mechanical properties vary and, therefore, using an anisotropic yield function is crucial. Since 1989 Frederic Barlat has developed a family of yield functions for constitutive modelling of plastic anisotropy. Among them, Yld2000-2D yield criteria has been applied for a wide range of sheet metals (e.g., aluminum alloys and advanced high-strength steels). The Yld2000-2D model is a non-quadratic type yield function based on two linear transformation of the stress tensor:

${\displaystyle \Phi =\Phi '(X')+\Phi ''(X'')=2{{\bar {\sigma }}^{a}}}$ :

The Yld2000-2D yield loci for a AA6022 T4 sheet.

where ${\displaystyle {\bar {\sigma }}}$ is the effective stress. and ${\displaystyle X'}$ and ${\displaystyle X''}$ are the transformed matrices (by linear transformation C or L):

${\displaystyle {\begin{array}{l}X'=C'.s=L'.\sigma \\X''=C''.s=L''.\sigma \end{array}}}$

where s is the deviatoric stress tensor.

for principal values of X’ and X”, the model could be expressed as:

${\displaystyle {\begin{array}{l}\Phi '={\left|{{{X'}_{1}}+{{X'}_{2}}}\right|^{a}}\\\Phi ''={\left|{2{{X''}_{2}}+{{X''}_{1}}}\right|^{a}}+{\left|{2{{X''}_{1}}+{{X''}_{2}}}\right|^{a}}\end{array}}\ }$

and:

${\displaystyle \left[{\begin{array}{*{20}{c}}{{L'}_{11}}\\{{L'}_{12}}\\{{L'}_{21}}\\{{L'}_{22}}\\{{L'}_{66}}\end{array}}\right]=\left[{\begin{array}{*{20}{c}}{2/3}&0&0\\{-1/3}&0&0\\0&{-1/3}&0\\0&{-2/3}&0\\0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{1}}\\{\alpha _{2}}\\{\alpha _{7}}\end{array}}\right],\left[{\begin{array}{*{20}{c}}{{L''}_{11}}\\{{L''}_{12}}\\{{L''}_{21}}\\{{L''}_{22}}\\{{L''}_{66}}\end{array}}\right]=\left[{\begin{array}{*{20}{c}}{-2}&2&8&{-2}&0\\1&{-4}&{-4}&4&0\\4&{-4}&{-4}&4&0\\{-2}&8&2&{-2}&0\\0&0&0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{3}}\\{\alpha _{4}}\\{\alpha _{5}}\\{\alpha _{6}}\\{\alpha _{8}}\end{array}}\right]}$

where ${\displaystyle \alpha _{1}...\alpha _{8}}$ are eight parameters of the Barlat's Yld2000-2D model to be identified with a set of experiments.