| ||||
|---|---|---|---|---|
| Cardinal | seventy-eight | |||
| Ordinal | 78th (seventy-eighth) | |||
| Factorization | 2 × 3 × 13 | |||
| Divisors | 1, 2, 3, 6, 13, 26, 39, 78 | |||
| Greek numeral | ΟΗ´ | |||
| Roman numeral | LXXVIII | |||
| Binary | 10011102 | |||
| Ternary | 22203 | |||
| Senary | 2106 | |||
| Octal | 1168 | |||
| Duodecimal | 6612 | |||
| Hexadecimal | 4E16 | |||
78 (seventy-eight) is the natural number following 77 and followed by 79.
In mathematics
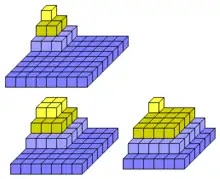
78 as the sum of four distinct nonzero squares
78 is:
- the 4th discrete tri-prime; or also termed Sphenic number, and the 4th of the form (2.3.r).[1]
- an abundant number with an aliquot sum of 90.
- a semiperfect number, as a multiple of a perfect number.
- the 12th triangular number.
- a palindromic number in bases 5 (3035), 7 (1417), 12 (6612), 25 (3325), and 38 (2238).
- a Harshad number in bases 3, 4, 5, 6, 7, 13 and 14.
- an Erdős–Woods number, since it is possible to find sequences of 78 consecutive integers such that each inner member shares a factor with either the first or the last member.[2]
- the dimension of the exceptional Lie group E6 and several related objects.
- the smallest number that can be expressed as the sum of four distinct nonzero squares in more than one way: , or (see image).[3][4]
77 and 78 form a Ruth–Aaron pair.
In science
- The atomic number of platinum.
In other fields
78 is also:
- In reference to gramophone records, 78 refers those meant to be spun at 78 revolutions per minute. Compare: LP, 33+1⁄3 and 45 rpm. 33 + 45 = 78
- A typical tarot deck containing the 21 trump cards, the Fool and the 56 suit cards make up 78 cards
- The Rule of 78s is a method of yearly interest calculation
- The number used by Martin Truex Jr. and Furniture Row Racing to win the 2017 Monster Energy NASCAR Cup Series championship and 2016 Coca-Cola 600. The team and driver Regan Smith also won the 2011 Showtime Southern 500 with 78. The number is now used by owner-driver B.J. McLeod for Live Fast Motorsports.
References
- ↑ "Sloane's A007304 : Sphenic numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-29.
- ↑ "Sloane's A059756 : Erdős-Woods numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-29.
- ↑ Sloane, N. J. A. (ed.). "Sequence A025386 (Numbers that are the sum of 4 distinct nonzero squares in 2 or more ways.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A025378 (Numbers that are the sum of 4 distinct nonzero squares in exactly 3 ways.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.