Simple pendulum

Consider the differential equation describing the motion of a simple pendulum:

${\displaystyle {d^{2}\theta \over dt^{2}}+{g \over \ell }\sin \theta =0.}$

where ${\displaystyle \ell }$ denotes the length of the pendulum, ${\displaystyle g}$ the gravitational acceleration and ${\displaystyle \theta }$ the angle between the pendulum and vertically downwards. In this system there is a conserved quantity H (the Hamiltonian), which is given by

${\displaystyle H={\frac {{\dot {\theta }}^{2}}{2}}-{\frac {g}{\ell }}\cos \theta .}$

With this defined, one can plot a curve of constant H in the phase space of system. The phase space is a graph with ${\displaystyle \theta }$ along the horizontal axis and ${\displaystyle {\dot {\theta }}}$ on the vertical axis – see the thumbnail to the right. The type of resulting curve depends upon the value of H.

The phase space for the simple pendulum

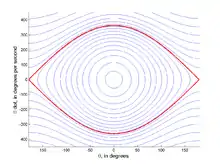
If ${\displaystyle H<-{\frac {g}{\ell }}}$ then no curve exists (because ${\displaystyle {\dot {\theta }}}$ must be imaginary).

If ${\displaystyle -{\frac {g}{\ell }}<H<{\frac {g}{\ell }}}$ then the curve will be a simple closed curve which is nearly circular for small H and becomes "eye" shaped when H approaches the upper bound. These curves correspond to the pendulum swinging periodically from side to side.

If ${\displaystyle {\frac {g}{\ell }}<H}$ then the curve is open, and this corresponds to the pendulum forever swinging through complete circles.

In this system the separatrix is the curve that corresponds to ${\displaystyle H={\frac {g}{\ell }}}$. It separates — hence the name — the phase space into two distinct areas, each with a distinct type of motion. The region inside the separatrix has all those phase space curves which correspond to the pendulum oscillating back and forth, whereas the region outside the separatrix has all the phase space curves which correspond to the pendulum continuously turning through vertical planar circles.

FitzHugh–Nagumo model

When ${\displaystyle b=2,I_{ext}=3.5}$, we can easily see the separatrix and the two basins of attraction by solving for the trajectories backwards in time.

In the FitzHugh–Nagumo model, when the linear nullcline pierces the cubic nullcline at the left, middle, and right branch once each, the system has a separatrix. Trajectories to the left of the separatrix converge to the left stable equilibrium, and similarly for the right. The separatrix itself is the stable manifold for the saddle point in the middle. Details are found in the page.

The separatrix is clearly visible by numerically solving for trajectories backwards in time. Since when solving for the trajectories forwards in time, trajectories diverge from the separatrix, when solving backwards in time, trajectories converge to the separatrix.