The current theoretical model of the atom involves a dense nucleus surrounded by a probabilistic "cloud" of electrons

Atomic theory is the scientific theory that matter is composed of particles called atoms. The concept that matter is composed of discrete particles is an ancient idea, but gained scientific credence in the 18th and 19th centuries when scientists found it could explain the behaviors of gases and how chemical elements reacted with each other. By the end of the 19th century, atomic theory had gained widespread acceptance in the scientific community.

The term "atom" comes from the Greek word atomos, which means "uncuttable". John Dalton applied the term to the basic units of mass of the chemical elements under the mistaken belief that chemical atoms are the fundamental particles in nature; it was another century before scientists realized that Dalton's so-called atoms have an underlying structure of their own. Particles which are truly indivisible are now referred to as "elementary particles".

History

Philosophical atomism

The basic idea that matter is made up of tiny indivisible particles is an old idea that appeared in many ancient cultures. The word atom is derived from the ancient Greek word atomos,[lower-alpha 1] which means "uncuttable". This ancient idea was based in philosophical reasoning rather than scientific reasoning. Modern atomic theory is not based on these old concepts.[1][2] In the early 19th century, the scientist John Dalton noticed that chemical elements seemed to combine with each other by discrete units of weight, and he decided to use the word "atom" to refer to these units, as he thought these were the fundamental units of matter.[3] About a century later it was discovered that Dalton's atoms are not actually indivisible, but the term stuck.

Dalton's law of multiple proportions

From A New System of Chemical Philosophy, 1808.

Near the end of the 18th century, two laws about chemical reactions emerged without referring to the notion of an atomic theory. The first was the law of conservation of mass, closely associated with the work of Antoine Lavoisier, which states that the total mass in a chemical reaction remains constant (that is, the reactants have the same mass as the products).[4] The second was the law of definite proportions. First established by the French chemist Joseph Proust in 1797 this law states that if a compound is broken down into its constituent chemical elements, then the masses of the constituents will always have the same proportions by weight, regardless of the quantity or source of the original substance.[5]

John Dalton studied data gathered by himself and other scientists and noticed a pattern that later came to be known as the law of multiple proportions. In compounds which all contain a particular element, the content of that element will differ across these compounds by ratios of small whole numbers. Dalton concluded from all this that elements react with each other in discrete and consistent units of weight. Borrowing the word from the philosophical tradition, Dalton called these units atoms.

Example 1 — tin oxides: There are two types of tin oxide: one is a grey powder that is 88.1% tin and 11.9% oxygen, and the other is a white powder that is 78.7% tin and 21.3% oxygen. Adjusting these figures, in the grey powder there is about 13.5 g of oxygen for every 100 g of tin, and in the white powder there is about 27 g of oxygen for every 100 g of tin. 13.5 and 27 form a ratio of 1:2. Dalton concluded that in these oxides, for every tin atom there are one or two oxygen atoms respectively (SnO and SnO2).[6][7]

Example 2 — iron oxides: Dalton identified two oxides of iron. There is one type of iron oxide that is a black powder which is 78.1% iron and 21.9% oxygen; and there is another iron oxide that is a red powder which is 70.4% iron and 29.6% oxygen. Adjusting these figures, in the black powder there is about 28 g of oxygen for every 100 g of iron, and in the red powder there is about 42 g of oxygen for every 100 g of iron. 28 and 42 form a ratio of 2:3. Dalton concluded that in these oxides, for every two atoms of iron, there are two or three atoms of oxygen respectively (Fe2O2 and Fe2O3).[lower-alpha 2][8][9]

Example 3 — nitrogen oxides: Dalton was aware of three oxides of nitrogen: "nitrous oxide", "nitrous gas", and "nitric acid".[10] These compounds are known today as nitrous oxide, nitric oxide, and nitrogen dioxide respectively. "Nitrous oxide" is 63.3% nitrogen and 36.7% oxygen, which means it has 80 g of oxygen for every 140 g of nitrogen. "Nitrous gas" is 44.05% nitrogen and 55.95% oxygen, which means there are 160 g of oxygen for every 140 g of nitrogen. "Nitric acid" is 29.5% nitrogen and 70.5% oxygen, which means it has 320 g of oxygen for every 140 g of nitrogen. 80 g, 160 g, and 320 g form a ratio of 1:2:4. The formulas for these compounds are N2O, NO, and NO2.[11][12]

Dalton's atomic theory

From the evidence provided by the law of multiple proportions Dalton developed his atomic theory. A central problem for the theory was to determine the relative weights of the atoms of various elements. The atomic weight of an element is the weight an atom of that element is compared to the weights of atoms of the other elements. Dalton and his contemporaries could not measure the absolute weight of atoms—i.e. their weight in grams—because atoms were far too small to be directly measured with the technologies that existed in the 19th century. Instead, they measured how heavy atoms of various elements were relative to atoms of hydrogen, which chemists of Dalton's day knew was the lightest element in nature.

Dalton estimated the atomic weights according to the mass ratios in which they combined, with the weight of the hydrogen atom taken conventionally as unity. However, Dalton did not realize that some elements exist as molecules in their natural pure form—-e.g. pure oxygen exists as O2. He also mistakenly believed that the simplest compound between any two elements is always one atom of each (so he thought water was HO, not H2O).[13] This, in addition to the limitations of his apparatus, flawed his results. For instance, in 1803 he believed that oxygen atoms were 5.5 times heavier than hydrogen atoms, because in water he measured 5.5 grams of oxygen for every 1 gram of hydrogen and believed the formula for water was HO. Adopting better data, in 1806 he concluded that the atomic weight of oxygen must actually be 7 rather than 5.5, and he retained this weight for the rest of his life. Others at this time had already concluded from more precise measurements that the oxygen atom must weigh 8 relative to hydrogen equals 1, if one assumes Dalton's formula for the water molecule (HO), or 16 if one assumes the modern water formula (H2O).[14]

The flaw in Dalton's theory was corrected in principle in 1811 by Amedeo Avogadro. Avogadro had proposed that equal volumes of any two gases, at equal temperature and pressure, contain equal numbers of molecules (in other words, the mass of a gas's particles does not affect the volume that it occupies).[15] Avogadro's hypothesis, now usually called Avogadro's law, provided a method for deducing the relative weights of the molecules of gaseous elements, for if the hypothesis is correct relative gas densities directly indicate the relative weights of the particles that compose the gases. This way of thinking led directly to a second hypothesis: the particles of certain elemental gases were not atoms, but molecules consisting of two atoms each; and when combining chemically these molecules often split in two. For instance, the fact that two liters of hydrogen will react with just one liter of oxygen to produce two liters of water vapor (at constant pressure and temperature) suggested that a single oxygen molecule must split in two in order to form two molecules of water. This also meant that the water molecule must be H2O. Thus, Avogadro was able to offer more accurate estimates of the atomic mass of oxygen and various other elements, and made a distinction between molecules and atoms. What we now call atoms Avogadro called "elementary molecules", and what we now call molecules Avogadro called "compound molecules".[16]

Opposition to atomic theory

Dalton's atomic theory was not immediately accepted by all scientists.

One problem was the lack of uniform nomenclature. The word "atom" implied indivisibility, but Dalton instead defined an atom as being the basic particle of any substance, which meant that "compound atoms" such as carbon dioxide could divided, as opposed to "elementary atoms".[17] Other scientists used their own nomenclature, which only added to the general confusion. For instance, J. J. Berzelius used the term "organic atoms" to refer to particles containing three or more elements, because he thought this only existed in organic compounds.[18]

A second problem was philosophical. Scientists in the 19th century had no way of directly observing atoms. They inferred the existence of atoms through indirect observations, such as Dalton's law of multiple proportions. Some Scientists, notably those who ascribed to the school of positivism, argued that scientists should not attempt to deduce the deeper reality of the universe, but only systemize what patterns they can directly observe. The anti-atomists argued that while atoms might be a useful abstraction for predicting how elements react, they do not reflect concrete reality.

Such scientists were sometimes known as "equivalentists", because they preferred the theory of equivalent weights, which is a generalization of Proust's law of definite proportions. For example, 1 gram of hydrogen will combine with 8 grams of oxygen to form 9 grams of water, therefore the equivalent weight of oxygen is 8 grams. This position was eventually quashed by two important advancements that happened later in the 19th century: the development of the periodic table and the discovery that molecules have an internal architecture that determines their properties.[19]

Dalton's law of multiple proportions was also shown to not be a universal law when it came to organic substances. For instance, in oleic acid there is 34 g of hydrogen for every 216 g of carbon, and in methane there is 72 g of hydrogen for every 216 g of carbon. 34 and 72 form a ratio of 17:36, which is not a ratio of small whole numbers. We know now that carbon-based substances can have very large molecules, larger than any the other elements can form. Oleic acid's formula is C18H34O2 and methane's is CH4.[20]

Isomerism

Scientists discovered some substances have the exact same chemical content but different properties. For instance, in 1827, Friedrich Wöhler discovered that silver fulminate and silver cyanate are both 107 parts silver, 12 parts carbon, 14 parts nitrogen, and 12 parts oxygen (we now know their formulas as both AgCNO). In 1830 Jöns Jacob Berzelius introduced the term isomerism to describe the phenomenon. In 1860, Louis Pasteur hypothesized that the molecules of isomers might have the same set of atoms but in different arrangements.[21]

In 1874, Jacobus Henricus van 't Hoff proposed that the carbon atom bonds to other atoms in a tetrahedral arrangement. Working from this, he explained the structures of organic molecules in such a way that he could predict how many isomers a compound could have. Consider, for example, pentane (C5H12). In van 't Hoff's way of modelling molecules, there are three possible configurations for pentane, and scientists did go on to discover three and only three isomers of pentane.[22][23]

n-pentane
isopentane
neopentane
Jacobus Henricus van 't Hoff's way of modelling molecular structures correctly predicted three possible isomers for pentane (C5H12).

Isomerism was not something that could be fully explained by alternative theories to atomic theory, such as radical theory and the theory of types.[24][25]

Mendeleev's periodic table

Dmitrii Mendeleev noticed that when he arranged the elements in a row according to their atomic weights, there was a certain periodicity to them.[26]: 117  For instance, the second element, lithium, had similar properties to the ninth element, sodium, and the sixteenth element, potassium — a period of seven. Likewise, beryllium, magnesium, and calcium were similar and all were seven places apart from each other on Mendeleev's table. Using these patterns, Mendeleev predicted the existence and properties of new elements, which were later discovered in nature: scandium, gallium, and germanium.[26]: 118  Moreover, the periodic table could predict how many atoms of other elements that an atom could bond with — e.g., germanium and carbon are in the same group on the table and their atoms both combine with two oxygen atoms each (GeO2 and CO2). Mendeleev found these patterns validated atomic theory because it showed that the elements could be categorized by their atomic weight. Inserting a new element into the middle of a period would break the parallel between that period and the next, and would also violate Dalton's law of multiple proportions.[27]

Mendeleev's periodic table from 1871.

In the modern periodic table, the periodicity of the elements mentioned above is eight rather than seven because the noble gases were not known back when Mendeleev devised his table. The rows also now have different lengths (2, 8, 18, and 32) to fit with quantum theory.

Brownian motion

In 1827, the British botanist Robert Brown observed that dust particles inside pollen grains floating in water constantly jiggled about for no apparent reason. In 1905, Albert Einstein theorized that this Brownian motion was caused by the water molecules continuously knocking the grains about, and developed a mathematical model to describe it. This model was validated experimentally in 1908 by French physicist Jean Perrin, who used Einstein's equations to determine the size of atoms.[28]

Kinetic diameters of various simple molecules
MoleculePerrin's measurements[29]Modern measurements
Helium1.7 × 10−10 m2.6 × 10−10 m
Argon2.7 × 10−10 m3.4 × 10−10 m
Mercury2.8 × 10−10 m3 × 10−10 m
Hydrogen2 × 10−10 m2.89 × 10−10 m
Oxygen2.6 × 10−10 m3.46 × 10−10 m
Nitrogen2.7 × 10−10 m3.64 × 10−10 m
Chlorine4 × 10−10 m3.20 × 10−10 m

Statistical mechanics

In order to introduce the Ideal gas law and statistical forms of physics, it was necessary to postulate the existence of atoms. In 1738, Swiss physicist and mathematician Daniel Bernoulli postulated that the pressure of gases and heat were both caused by the underlying motion of molecules.

In 1860, James Clerk Maxwell, who was a vocal proponent of atomism, was the first to use statistical mechanics in physics.[30] Ludwig Boltzmann and Rudolf Clausius expanded his work on gases and the laws of Thermodynamics especially the second law relating to entropy. In the 1870s, Josiah Willard Gibbs extended the laws of entropy and thermodynamics and coined the term "statistical mechanics." Einstein later independently reinvented Gibbs' laws, because they had only been printed in an obscure American journal.[31] Einstein later commented that had he known of Gibbs' work, he would "not have published those papers at all, but confined myself to the treatment of some few points [that were distinct]."[32] All of statistical mechanics and the laws of heat, gas, and entropy took the existence of atoms as a necessary postulate.

Discovery of subatomic particles

The cathode rays (blue) were emitted from the cathode, sharpened to a beam by the slits, then deflected as they passed between the two electrified plates.

Atoms were thought to be the smallest possible division of matter until 1897 when J. J. Thomson discovered the electron through his work on cathode rays.[33]

A Crookes tube is a sealed glass container in which two electrodes are separated by a vacuum. When a voltage is applied across the electrodes, cathode rays are generated, creating a glowing patch where they strike the glass at the opposite end of the tube. Through experimentation, Thomson discovered that the rays could be deflected by an electric field (in addition to magnetic fields, which was already known). He concluded that these rays, rather than being a form of light, were composed of very light negatively charged particles. Thomson called these "corpuscles", but other scientists called them electrons, following an 1894 suggestion by George Johnstone Stoney for naming the basic unit of electrical charge.[34] He measured the mass-to-charge ratio and discovered it was 1800 times smaller than that of hydrogen, the smallest atom. These corpuscles were a particle unlike any other previously known.

Thomson suggested that atoms were divisible, and that the corpuscles were their building blocks.[35] To explain the overall neutral charge of the atom, he proposed that the corpuscles were distributed in a uniform sea of positive charge.[36] This became known as the plum pudding model as the electrons were embedded in the positive charge like bits of fruit in a dried-fruit pudding, though Thomson thought the electrons moved about within the atom.[37]

Discovery of the nucleus

The Geiger–Marsden experiment
Left: Expected results: alpha particles passing through the plum pudding model of the atom with negligible deflection.
Right: Observed results: a small portion of the particles were deflected by the concentrated positive charge of the nucleus.

Thomson's plum pudding model was disproved in 1909 by one of his former students, Ernest Rutherford, who discovered that most of the mass and positive charge of an atom is concentrated in a very small fraction of its volume, which he assumed to be at the very center.

Ernest Rutherford and his colleagues Hans Geiger and Ernest Marsden came to have doubts about the Thomson model after they encountered difficulties when they tried to build an instrument to measure the charge-to-mass ratio of alpha particles (these are positively-charged particles emitted by certain radioactive substances such as radium). The alpha particles were being scattered by the air in the detection chamber, which made the measurements unreliable. Thomson had encountered a similar problem in his work on cathode rays, which he solved by creating a near-perfect vacuum in his instruments. Rutherford didn't think he'd run into this same problem because alpha particles are much heavier than electrons. According to Thomson's model of the atom, the positive charge in the atom is not concentrated enough to produce an electric field strong enough to deflect an alpha particle, and the electrons are so lightweight they should be pushed aside effortlessly by the much heavier alpha particles. Yet there was scattering, so Rutherford and his colleagues decided to investigate this scattering carefully.[38]

Between 1908 and 1913, Rutherford and his colleagues performed a series of experiments in which they bombarded thin foils of metal with alpha particles. They spotted alpha particles being deflected by angles greater than 90°. To explain this, Rutherford proposed that the positive charge of the atom is not distributed throughout the atom's volume as Thomson believed, but is concentrated in a tiny nucleus at the center. Only such an intense concentration of charge could produce an electric field strong enough to deflect the alpha particles as observed.[38] Rutherford's model is sometimes called the "planetary model".[39] However, Hantaro Nagaoka was quoted by Rutherford as the first to suggest a planetary atom in 1904.[40] And planetary models had been suggested as early as 1897 such as the one by Joseph Larmor.[41] Probably the earliest solar system model was found in an unpublished note by Ludwig August Colding in 1854 whose idea was that atoms were analogous to planetary systems that rotate and cause magnetic polarity.[42]

First steps toward a quantum physical model of the atom

The planetary model of the atom had two significant shortcomings. The first is that, unlike planets orbiting a sun, electrons are charged particles. An accelerating electric charge is known to emit electromagnetic waves according to the Larmor formula in classical electromagnetism. An orbiting charge should steadily lose energy and spiral toward the nucleus, colliding with it in a small fraction of a second. The second problem was that the planetary model could not explain the highly peaked emission and absorption spectra of atoms that were observed.

The Bohr model of the atom

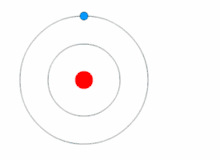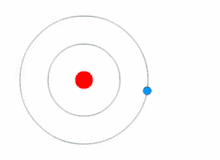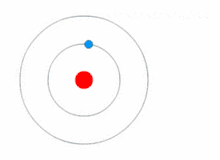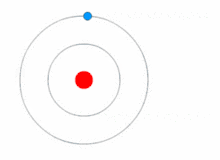
Quantum theory revolutionized physics at the beginning of the 20th century, when Max Planck and Albert Einstein postulated that light energy is emitted or absorbed in discrete amounts known as quanta (singular, quantum). This led to a series of quantum atomic models such as the quantum model of Arthur Erich Haas in 1910 and the 1912 John William Nicholson quantum atomic model that quantized angular momentum as h/2π.[43][44] In 1913, Niels Bohr incorporated this idea into his Bohr model of the atom, in which an electron could only orbit the nucleus in particular circular orbits with fixed angular momentum and energy, its distance from the nucleus (i.e., their radii) being proportional to its energy.[45] Under this model an electron could not spiral into the nucleus because it could not lose energy in a continuous manner; instead, it could only make instantaneous "quantum leaps" between the fixed energy levels.[45] When this occurred, light was emitted or absorbed at a frequency proportional to the change in energy (hence the absorption and emission of light in discrete spectra).[45]

Bohr's model was not perfect. It could only predict the spectral lines of hydrogen, not those of multielectron atoms.[46] Worse still, it could not even account for all features of the hydrogen spectrum: as spectrographic technology improved, it was discovered that applying a magnetic field caused spectral lines to multiply in a way that Bohr's model couldn't explain. In 1916, Arnold Sommerfeld added elliptical orbits to the Bohr model to explain the extra emission lines, but this made the model very difficult to use, and it still couldn't explain more complex atoms.[47][48]

Discovery of isotopes

While experimenting with the products of radioactive decay, in 1913 radiochemist Frederick Soddy discovered that there appeared to be more than one variety of some elements.[49] The term isotope was coined by Margaret Todd as a suitable name for these varieties.[50]

That same year, J. J. Thomson conducted an experiment in which he channeled a stream of neon ions through magnetic and electric fields, striking a photographic plate at the other end. He observed two glowing patches on the plate, which suggested two different deflection trajectories. Thomson concluded this was because some of the neon ions had a different mass.[51] The nature of this differing mass would later be explained by the discovery of neutrons in 1932: all atoms of the same element contain the same number of protons, while different isotopes have different numbers of neutrons.[52]

Discovery of nuclear particles

In 1917 Rutherford bombarded nitrogen gas with alpha particles and observed hydrogen nuclei being emitted from the gas (Rutherford recognized these, because he had previously obtained them bombarding hydrogen with alpha particles, and observing hydrogen nuclei in the products). Rutherford concluded that the hydrogen nuclei emerged from the nuclei of the nitrogen atoms themselves (in effect, he had split a nitrogen).[53]

From his own work and the work of his students Bohr and Henry Moseley, Rutherford knew that the positive charge of any atom could always be equated to that of an integer number of hydrogen nuclei. This, coupled with the atomic mass of many elements being roughly equivalent to an integer number of hydrogen atoms - then assumed to be the lightest particles - led him to conclude that hydrogen nuclei were singular particles and a basic constituent of all atomic nuclei. He named such particles protons. Further experimentation by Rutherford found that the nuclear mass of most atoms exceeded that of the protons it possessed; he speculated that this surplus mass was composed of previously-unknown neutrally charged particles, which were tentatively dubbed "neutrons".

In 1928, Walter Bothe observed that beryllium emitted a highly penetrating, electrically neutral radiation when bombarded with alpha particles. It was later discovered that this radiation could knock hydrogen atoms out of paraffin wax. Initially it was thought to be high-energy gamma radiation, since gamma radiation had a similar effect on electrons in metals, but James Chadwick found that the ionization effect was too strong for it to be due to electromagnetic radiation, so long as energy and momentum were conserved in the interaction. In 1932, Chadwick exposed various elements, such as hydrogen and nitrogen, to the mysterious "beryllium radiation", and by measuring the energies of the recoiling charged particles, he deduced that the radiation was actually composed of electrically neutral particles which could not be massless like the gamma ray, but instead were required to have a mass similar to that of a proton. Chadwick now claimed these particles as Rutherford's neutrons.[54] For his discovery of the neutron, Chadwick received the Nobel Prize in 1935.[55]

Quantum physical models of the atom

The five filled atomic orbitals of a neon atom separated and arranged in order of increasing energy from left to right, with the last three orbitals being equal in energy. Each orbital holds up to two electrons, which most probably exist in the zones represented by the colored bubbles. Each electron is equally present in both orbital zones, shown here by color only to highlight the different wave phase.

In 1924, Louis de Broglie proposed that all moving particles—particularly subatomic particles such as electrons—exhibit a degree of wave-like behavior. Erwin Schrödinger, fascinated by this idea, explored whether or not the movement of an electron in an atom could be better explained as a wave rather than as a particle. Schrödinger's equation, published in 1926,[56] describes an electron as a wave function instead of as a point particle. This approach elegantly predicted many of the spectral phenomena that Bohr's model failed to explain. Although this concept was mathematically convenient, it was difficult to visualize, and faced opposition.[57] One of its critics, Max Born, proposed instead that Schrödinger's wave function did not describe the physical extent of an electron (like a charge distribution in classical electromagnetism), but rather gave the probability that an electron would, when measured, be found at a particular point.[58] This reconciled the ideas of wave-like and particle-like electrons: the behavior of an electron, or of any other subatomic entity, has both wave-like and particle-like aspects, and whether one aspect or the other is more apparent depends upon the situation.[59]

A consequence of describing electrons as waveforms is that it is mathematically impossible to simultaneously derive the position and momentum of an electron. This became known as the Heisenberg uncertainty principle after the theoretical physicist Werner Heisenberg, who first published a version of it in 1927.[60] (Heisenberg analyzed a thought experiment where one attempts to measure an electron's position and momentum simultaneously. However, Heisenberg did not give precise mathematical definitions of what the "uncertainty" in these measurements meant. The precise mathematical statement of the position-momentum uncertainty principle is due to Earle Hesse Kennard, Wolfgang Pauli, and Hermann Weyl.[61][62]) This invalidated Bohr's model, with its neat, clearly defined circular orbits. The modern model of the atom describes the positions of electrons in an atom in terms of probabilities. An electron can potentially be found at any distance from the nucleus, but, depending on its energy level and angular momentum, exists more frequently in certain regions around the nucleus than others; this pattern is referred to as its atomic orbital. The orbitals come in a variety of shapes—sphere, dumbbell, torus, etc.—with the nucleus in the middle.[63] The shapes of atomic orbitals are found by solving the Schrödinger equation; however, analytic solutions of the Schrödinger equation are known for very few relatively simple model Hamiltonians including the hydrogen atom and the dihydrogen cation. Even the helium atom—which contains just two electrons—has defied all attempts at a fully analytic treatment.[64][65][66]

See also

Footnotes

  1. ↑ a combination of the negative term "a-" and "τομή," the term for "cut"
  2. ↑ Iron(II) oxide's formula is written here as "Fe2O2" rather than the more conventional "FeO" because this better illustrates the explanation.
  1. ↑ Pullman, Bernard (1998). The Atom in the History of Human Thought. Oxford, England: Oxford University Press. pp. 31–33. ISBN 978-0-19-515040-7. Archived from the original on 5 February 2021. Retrieved 25 October 2020.
  2. ↑ Melsen (1952). From Atomos to Atom, pp. 18–19
  3. ↑ Pullman (1998). The Atom in the History of Human Thought, p. 198: "Dalton reaffirmed that atoms are indivisible and indestructible and are the ultimate constituents of matter."
  4. ↑ Weisstein, Eric W. "Lavoisier, Antoine (1743-1794)". scienceworld.wolfram.com. Retrieved 2009-08-01.
  5. ↑ "Law of definite proportions | chemistry". Encyclopedia Britannica. Retrieved 2020-09-03.
  6. ↑ Dalton (1817). A New System of Chemical Philosophy vol. 2, p. 36
  7. ↑ Melsen (1952). From Atomos to Atom, p. 137
  8. ↑ Dalton (1817). A New System of Chemical Philosophy vol. 2, p. 28
  9. ↑ Millington (1906). John Dalton, p. 113
  10. ↑ Dalton (1808). A New System of Chemical Philosophy vol. 1, pp. 316-319
  11. ↑ Dalton (1808). A New System of Chemical Philosophy vol. 1, pp. 316–319
  12. ↑ Holbrow et al. (2010). Modern Introductory Physics, pp. 65–66
  13. ↑ Johnson, Chris. "Avogadro - his contribution to chemistry". Archived from the original on 2002-07-10. Retrieved 2009-08-01.
  14. ↑ Alan J. Rocke (1984). Chemical Atomism in the Nineteenth Century. Columbus: Ohio State University Press.
  15. ↑ Avogadro, Amedeo (1811). "Essay on a Manner of Determining the Relative Masses of the Elementary Molecules of Bodies, and the Proportions in Which They Enter into These Compounds". Journal de Physique. 73: 58–76.
  16. ↑ Hinshelwood, Cyril N.; Pauling, Linus (1956-10-19). "Amedeo Avogadro". Science. 124 (3225): 708–713. Bibcode:1956Sci...124..708H. doi:10.1126/science.124.3225.708. ISSN 0036-8075. PMID 17757602.
  17. ↑ Pullman (1998). The Atom in the History of Human Thought, p. 201
  18. ↑ Pullman (1998). The Atom in the History of Human Thought, p. 202
  19. ↑ Pullman (1998). The Atom in the History of Human Thought, p. 226: "The first development is the establishment of the periodic classification of the elements, marking the successful climax of concerted efforts to arrange the chemical properties of elements according to their atomic weight. The second is the emergence of structural chemistry, which ousted what was a simple and primitive verbal description of the elemental composition, be it atomic or equivalentist, of substances and replaced it with a systematic determination of their internal architecture."
  20. ↑ Trusted (1999). The Mystery of Matter, p. 73
  21. ↑ Pullman (1998). The Atom in the History of Human Thought, p. 230
  22. ↑ Melsen (1952). From Atomos to Atom, pp. 147–148
  23. ↑ Henry Enfield Roscoe, Carl Schorlemmer (1895). A Treatise on Chemistry, Volume 3, Part 1, pp. 121–122
  24. ↑ Henry Enfield Roscoe, Carl Schorlemmer (1895). A Treatise on Chemistry, Volume 3, Part 1, pp. 121: "The radical theory and the theory of types are capable of explaining many cases of isomerism, but it was not until the doctrine of the linking of atoms was established that a clear light was thrown on this subject."
  25. ↑ Adolphe Wurtz (1880). The Atomic Theory, p. 291: "It is in this manner that the theory of atomicity predicts, interprets, and limits the number of isomers; it has furnished the elements of one of the greatest advances which science has accomplished in the last twenty years. [...] The theory of atomicity has successfully attacked the problem by introducing into the discussion exact data, which have been in a great number of cases confirmed by experiment."
  26. 1 2 Scerri, Eric R. (2020). The Periodic Table, Its Story and Its Significance (2nd ed.). New York: Oxford University Press. ISBN 978-0-190-91436-3.
  27. ↑ Brito, Angmary; Rodríguez, María A.; Niaz, Mansoor (2005). "A Reconstruction of Development of the Periodic Table Based on History and Philosophy of Science and Its Implications for General Chemistry Textbooks". Journal of Research in Science Teaching. 42 (1): 84–111. Bibcode:2005JRScT..42...84B. doi:10.1002/tea.20044.
  28. ↑ "The Nobel Prize in Physics 1926". NobelPrize.org. Retrieved 2023-02-08.
  29. ↑ Perrin (1909). Brownian Movement and Molecular Reality, p. 50
  30. ↑ See:
  31. ↑ Navarro, Luis. “Gibbs, Einstein and the Foundations of Statistical Mechanics.” Archive for History of Exact Sciences, vol. 53, no. 2, Springer, 1998, pp. 147–80, http://www.jstor.org/stable/41134058.
  32. ↑ Stone, A. Douglas, Einstein and the quantum : the quest of the valiant Swabian, Princeton University Press, (2013). ISBN 978-0-691-13968-5 quoted from Folsing, Albert Einstein, 110.
  33. ↑ Thomson, J. J. (1897). "Cathode rays" ([facsimile from Stephen Wright, Classical Scientific Papers, Physics (Mills and Boon, 1964)]). Philosophical Magazine. 44 (269): 293. doi:10.1080/14786449708621070.
  34. ↑ Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (1986-12-26). Beyond the Mechanical Universe: From Electricity to Modern Physics. Cambridge University Press. p. 435. ISBN 978-0-521-30430-6.
  35. ↑ Whittaker, E. T. (1951), A History of the Theories of Aether and Electricity. Vol 1, Nelson, London
  36. ↑ Thomson, J. J. (1904). "On the Structure of the Atom: an Investigation of the Stability and Periods of Oscillation of a number of Corpuscles arranged at equal intervals around the Circumference of a Circle; with Application of the Results to the Theory of Atomic Structure". Philosophical Magazine. 7 (39): 237. doi:10.1080/14786440409463107.
  37. ↑ Hon, Giora; Goldstein, Bernard R. (2013-09-06). "J. J. Thomson's plum-pudding atomic model: The making of a scientific myth". Annalen der Physik. 525 (8–9): A129–A133. Bibcode:2013AnP...525A.129H. doi:10.1002/andp.201300732. S2CID 119853037.
  38. 1 2 Heilbron (2003). Ernest Rutherford and the Explosion of Atoms, pp. 64-68
  39. ↑ "Rutherford model | Definition & Facts". Encyclopedia Britannica. Retrieved 23 August 2021.
  40. ↑ Rutherford either knew the article or looked it up, for he cited it on the last page of his classic paper, "The Scattering of a and b Particles by Matter and the Structure of the Atom," Phil. Mag., 21 (1911), 669.
  41. ↑ Larmor, Joseph (1897), "On a Dynamical Theory of the Electric and Luminiferous Medium, Part 3, Relations with material media" , Philosophical Transactions of the Royal Society, 190: 205–300, Bibcode:1897RSPTA.190..205L, doi:10.1098/rsta.1897.0020 “…that of the transmission of radiation across a medium permeated by molecules, each consisting of a system of electrons in steady orbital motion, and each capable of free oscillations about the steady state of motion with definite free periods analogous to those of the planetary inequalities of the Solar System;”
  42. ↑ Helge Kragh, Niels Bohr and the Quantum Atom: The Bohr Model of Atomic Structure 1913–1925, 2012, Chap. 1, ISBN 9780199654987, Oxford Scholarship Online, doi:10.1093/acprof:oso/9780199654987.001.0001
  43. ↑ J. W. Nicholson, Month. Not. Roy. Astr. Soc. lxxii. pp. 49,130, 677, 693, 729 (1912).
  44. ↑ The Atomic Theory of John William Nicholson, Russell McCormmach, Archive for History of Exact Sciences, Vol. 3, No. 2 (25.8.1966), pp. 160-184 (25 pages), Springer.
  45. 1 2 3 Bohr, Niels (1913). "On the constitution of atoms and molecules" (PDF). Philosophical Magazine. 26 (153): 476–502. Bibcode:1913PMag...26..476B. doi:10.1080/14786441308634993. Archived (PDF) from the original on 2022-10-09.
  46. ↑ Kragh, Helge (1979). "Niels Bohr's Second Atomic Theory". Historical Studies in the Physical Sciences. 10: 123–186. doi:10.2307/27757389. ISSN 0073-2672. JSTOR 27757389.
  47. ↑ Hentschel, Klaus (2009). "Zeeman Effect". In Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel (eds.). Compendium of Quantum Physics. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 862–864. doi:10.1007/978-3-540-70626-7_241. ISBN 978-3-540-70622-9. Retrieved 2023-02-08.
  48. ↑ Eckert, Michael (April 2014). "How Sommerfeld extended Bohr's model of the atom (1913–1916)". The European Physical Journal H. 39 (2): 141–156. Bibcode:2014EPJH...39..141E. doi:10.1140/epjh/e2013-40052-4. ISSN 2102-6459. S2CID 256006474.
  49. ↑ "Frederick Soddy, The Nobel Prize in Chemistry 1921". Nobel Foundation. Retrieved 2008-01-18.
  50. ↑ Fleck, Alexander (1957). "Frederick Soddy". Biographical Memoirs of Fellows of the Royal Society. 3: 203–216. doi:10.1098/rsbm.1957.0014. p. 208: Up to 1913 we used the phrase 'radio elements chemically non-separable' and at that time the word isotope was suggested in a drawing-room discussion with Dr. Margaret Todd in the home of Soddy's father-in-law, Sir George Beilby.
  51. ↑ Thomson, J. J. (1913). "Rays of positive electricity". Proceedings of the Royal Society. A 89 (607): 1–20. Bibcode:1913RSPSA..89....1T. doi:10.1098/rspa.1913.0057. S2CID 124295244. [as excerpted in Henry A. Boorse & Lloyd Motz, The World of the Atom, Vol. 1 (New York: Basic Books, 1966)]. Retrieved on August 29, 2007.
  52. ↑ Flowers, Paul; et al. (2022). Chemistry 2e. OpenStax. pp. 70–71. ISBN 978-1-947172-61-6.
  53. ↑ Rutherford, Ernest (1919). "Collisions of alpha Particles with Light Atoms. IV. An Anomalous Effect in Nitrogen". Philosophical Magazine. 37 (222): 581. doi:10.1080/14786440608635919.
  54. ↑ Chadwick, James (1932). "Possible Existence of a Neutron" (PDF). Nature. 129 (3252): 312. Bibcode:1932Natur.129Q.312C. doi:10.1038/129312a0. S2CID 4076465. Archived (PDF) from the original on 2022-10-09.
  55. ↑ "The Nobel Prize in Physics 1935". NobelPrize.org. Retrieved 2023-02-08.
  56. ↑ Schrödinger, Erwin (1926). "Quantisation as an Eigenvalue Problem". Annalen der Physik. 81 (18): 109–139. Bibcode:1926AnP...386..109S. doi:10.1002/andp.19263861802.
  57. ↑ Mahanti, Subodh. "Erwin Schrödinger: The Founder of Quantum Wave Mechanics". Archived from the original on 2009-04-17. Retrieved 2009-08-01.
  58. ↑ Mahanti, Subodh. "Max Born: Founder of Lattice Dynamics". Archived from the original on 2009-01-22. Retrieved 2009-08-01.
  59. ↑ Greiner, Walter (4 October 2000). "Quantum Mechanics: An Introduction". Springer. ISBN 9783540674580. Retrieved 2010-06-14.
  60. ↑ Heisenberg, W. (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Zeitschrift für Physik (in German). 43 (3–4): 172–198. Bibcode:1927ZPhy...43..172H. doi:10.1007/BF01397280. S2CID 122763326.
  61. ↑ Busch, Paul; Lahti, Pekka; Werner, Reinhard F. (17 October 2013). "Proof of Heisenberg's Error-Disturbance Relation". Physical Review Letters. 111 (16): 160405. arXiv:1306.1565. Bibcode:2013PhRvL.111p0405B. doi:10.1103/PhysRevLett.111.160405. ISSN 0031-9007. PMID 24182239. S2CID 24507489.
  62. ↑ Appleby, David Marcus (6 May 2016). "Quantum Errors and Disturbances: Response to Busch, Lahti and Werner". Entropy. 18 (5): 174. arXiv:1602.09002. Bibcode:2016Entrp..18..174A. doi:10.3390/e18050174.
  63. ↑ Milton Orchin; Roger Macomber; Allan Pinhas; R. Wilson. "The Vocabulary and Concepts of Organic Chemistry, Second Edition" (PDF). Archived (PDF) from the original on 2022-10-09. Retrieved 2010-06-14.
  64. ↑ Zwiebach, Barton (2022). Mastering Quantum Mechanics Essentials, Theory, and Applications. Cambridge: MIT Press. pp. 281–305. ISBN 978-0-262-36689-2. OCLC 1306066387.
  65. ↑ Grivet, Jean-Philippe (January 2002). "The Hydrogen Molecular Ion Revisited". Journal of Chemical Education. 79 (1): 127. Bibcode:2002JChEd..79..127G. doi:10.1021/ed079p127. ISSN 0021-9584.
  66. ↑ Levin, F. S.; Shertzer, J. (1985-12-01). "Finite-element solution of the Schrödinger equation for the helium ground state". Physical Review A. 32 (6): 3285–3290. Bibcode:1985PhRvA..32.3285L. doi:10.1103/PhysRevA.32.3285. ISSN 0556-2791. PMID 9896495.

Bibliography

  • Andrew G. van Melsen (1960) [First published 1952]. From Atomos to Atom: The History of the Concept Atom. Translated by Henry J. Koren. Dover Publications. ISBN 0-486-49584-1.
  • J. P. Millington (1906). John Dalton. J. M. Dent & Co. (London); E. P. Dutton & Co. (New York).
  • Jaume Navarro (2012). A History of the Electron: J. J. and G. P. Thomson. Cambridge University Press. ISBN 978-1-107-00522-8.
  • Jennifer Trusted (1999). The Mystery of Matter. MacMillan. ISBN 0-333-76002-6.
  • Bernard Pullman (1998). The Atom in the History of Human Thought. Translated by Axel Reisinger. Oxford University Press. ISBN 0-19-511447-7.
  • Jean Perrin (1910) [1909]. Brownian Movement and Molecular Reality. Translated by F. Soddy. Taylor and Francis.

Further reading

Wikiquote has quotations related to Atomic theory.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.