Conic section

A degenerate conic is a conic section (a second-degree plane curve, defined by a polynomial equation of degree two) that fails to be an irreducible curve.

• A point is a degenerate circle, namely one with radius 0.^[1]
• The line is a degenerate case of a parabola if the parabola resides on a tangent plane. In inversive geometry, a line is a degenerate case of a circle, with infinite radius.
• Two parallel lines also form a degenerate parabola.
• A line segment can be viewed as a degenerate case of an ellipse in which the semiminor axis goes to zero, the foci go to the endpoints, and the eccentricity goes to one.
• A circle can be thought of as a degenerate ellipse, as the eccentricity approaches 0 and the foci merge.^[1]
• An ellipse can also degenerate into a single point.
• A hyperbola can degenerate into two lines crossing at a point, through a family of hyperbolae having those lines as common asymptotes.

Triangle

The three types of degenerate triangles, all of which contain zero area.

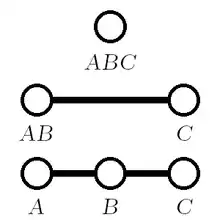
• A degenerate triangle has collinear vertices^[3] and zero area, and thus coincides with a segment covered twice (if the three vertices are not all equal; otherwise, the triangle degenerates to a single point). If the three vertices are pairwise distinct, it has two 0° angles and one 180° angle. If two vertices are equal, it has one 0° angle and two undefined angles.

Rectangle

• A line segment is a degenerate case of a rectangle which has a side of length 0.
• For any non-empty subset ${\displaystyle S\subseteq \{1,2,\ldots ,n\}}$, there is a bounded, axis-aligned degenerate rectangle
  $${\displaystyle R\triangleq \left\{\mathbf {x} \in \mathbb {R} ^{n}:x_{i}=c_{i}\ ({\text{for }}i\in S){\text{ and }}a_{i}\leq x_{i}\leq b_{i}\ ({\text{for }}i\notin S)\right\}}$$

  
  where ${\displaystyle \mathbf {x} \triangleq \left[x_{1},x_{2},\ldots ,x_{n}\right]}$ and a_i, b_i, c_i are constant (with a_i ≤ b_i for all i). The number of degenerate sides of R is the number of elements of the subset S. Thus, there may be as few as one degenerate "side" or as many as n (in which case R reduces to a singleton point).

Convex polygon

• A convex polygon is degenerate if at least two consecutive sides coincide at least partially, or at least one side has zero length, or at least one angle is 180°. Thus a degenerate convex polygon of n sides looks like a polygon with fewer sides. In the case of triangles, this definition coincides with the one that has been given above.

Convex polyhedron

• A convex polyhedron is degenerate if either two adjacent facets are coplanar or two edges are aligned. In the case of a tetrahedron, this is equivalent to saying that all of its vertices lie in the same plane, giving it a volume of zero.

Standard torus

• In contexts where self-intersection is allowed, a double-covered sphere is a degenerate standard torus where the axis of revolution passes through the center of the generating circle, rather than outside it.
• A torus degenerates to a circle when its minor radius goes to 0.

Sphere

• When the radius of a sphere goes to zero, the resulting degenerate sphere of zero volume is a point.

Other

• See general position for other examples.