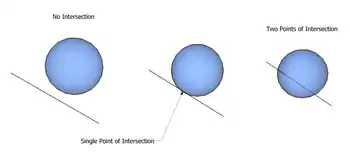
The three possible line-sphere intersections:
1. No intersection.
2. Point intersection.
3. Two point intersection.

In analytic geometry, a line and a sphere can intersect in three ways:

1. No intersection at all
2. Intersection in exactly one point
3. Intersection in two points.

Methods for distinguishing these cases, and determining the coordinates for the points in the latter cases, are useful in a number of circumstances. For example, it is a common calculation to perform during ray tracing.^[1]

Calculation using vectors in 3D

In vector notation, the equations are as follows:

Equation for a sphere

${\displaystyle \left\Vert \mathbf {x} -\mathbf {c} \right\Vert ^{2}=r^{2}}$

• ${\displaystyle \mathbf {x} }$ : points on the sphere
• ${\displaystyle \mathbf {c} }$ : center point
• ${\displaystyle r}$ : radius of the sphere

Equation for a line starting at ${\displaystyle \mathbf {o} }$

${\displaystyle \mathbf {x} =\mathbf {o} +d\mathbf {u} }$

• ${\displaystyle \mathbf {x} }$ : points on the line
• ${\displaystyle \mathbf {o} }$ : origin of the line
• ${\displaystyle d}$ : distance from the origin of the line
• ${\displaystyle \mathbf {u} }$ : direction of line (a non-zero vector)

Searching for points that are on the line and on the sphere means combining the equations and solving for ${\displaystyle d}$, involving the dot product of vectors:

Equations combined

${\displaystyle \left\Vert \mathbf {o} +d\mathbf {u} -\mathbf {c} \right\Vert ^{2}=r^{2}\Leftrightarrow (\mathbf {o} +d\mathbf {u} -\mathbf {c} )\cdot (\mathbf {o} +d\mathbf {u} -\mathbf {c} )=r^{2}}$

Expanded and rearranged:

${\displaystyle d^{2}(\mathbf {u} \cdot \mathbf {u} )+2d[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]+(\mathbf {o} -\mathbf {c} )\cdot (\mathbf {o} -\mathbf {c} )-r^{2}=0}$

The form of a quadratic formula is now observable. (This quadratic equation is an instance of Joachimsthal's equation.^[2])

${\displaystyle ad^{2}+bd+c=0}$

where

• ${\displaystyle a=\mathbf {u} \cdot \mathbf {u} =\left\Vert \mathbf {u} \right\Vert ^{2}}$
• ${\displaystyle b=2[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]}$
• ${\displaystyle c=(\mathbf {o} -\mathbf {c} )\cdot (\mathbf {o} -\mathbf {c} )-r^{2}=\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2}}$

Simplified

${\displaystyle d={\frac {-2[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]\pm {\sqrt {(2[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )])^{2}-4\left\Vert \mathbf {u} \right\Vert ^{2}(\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2})}}}{2\left\Vert \mathbf {u} \right\Vert ^{2}}}={\frac {-[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]\pm {\sqrt {(\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} ))^{2}-\left\Vert \mathbf {u} \right\Vert ^{2}(\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2})}}}{\left\Vert \mathbf {u} \right\Vert ^{2}}}}$

Note that in the specific case where ${\displaystyle \mathbf {u} }$ is a unit vector, and thus ${\displaystyle \left\Vert \mathbf {u} \right\Vert ^{2}=1}$, we can simplify this further to (writing ${\displaystyle {\hat {\mathbf {u} }}}$ instead of ${\displaystyle \mathbf {u} }$ to indicate a unit vector):

${\displaystyle \nabla =[{\hat {\mathbf {u} }}\cdot (\mathbf {o} -\mathbf {c} )]^{2}-(\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2})}$

${\displaystyle d=-[{\hat {\mathbf {u} }}\cdot (\mathbf {o} -\mathbf {c} )]\pm {\sqrt {\nabla }}}$

• If ${\displaystyle \nabla <0}$, then it is clear that no solutions exist, i.e. the line does not intersect the sphere (case 1).
• If ${\displaystyle \nabla =0}$, then exactly one solution exists, i.e. the line just touches the sphere in one point (case 2).
• If ${\displaystyle \nabla >0}$, two solutions exist, and thus the line touches the sphere in two points (case 3).

See also

• Intersection_(geometry)#A_line_and_a_circle
• Analytic geometry
• Line–plane intersection
• Plane–plane intersection
• Plane–sphere intersection

References