General relativity
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }}$
Introduction History Timeline Tests Mathematical formulation
Fundamental concepts Equivalence principle Special relativity World line Pseudo-Riemannian manifold
Phenomena Kepler problem Gravitational lensing Gravitational waves Frame-dragging Geodetic effect Event horizon Singularity Black hole Spacetime Spacetime diagrams Minkowski spacetime Einstein–Rosen bridge
Equations Formalisms Equations Linearized gravity Einstein field equations Friedmann Geodesics Mathisson–Papapetrou–Dixon Hamilton–Jacobi–Einstein Formalisms ADM BSSN Post-Newtonian Advanced theory Kaluza–Klein theory Quantum gravity
Solutions Schwarzschild (interior) Reissner–Nordström Gödel Kerr Kerr–Newman Kerr–Newman–de Sitter Kasner Lemaître–Tolman Taub–NUT Milne Robertson–Walker Oppenheimer–Snyder pp-wave van Stockum dust Weyl−Lewis−Papapetrou
Scientists Einstein Lorentz Hilbert Poincaré Schwarzschild de Sitter Reissner Nordström Weyl Eddington Friedman Milne Zwicky Lemaître Oppenheimer Gödel Wheeler Robertson Bardeen Walker Kerr Chandrasekhar Ehlers Penrose Hawking Raychaudhuri Taylor Hulse van Stockum Taub Newman Yau Thorne others
Physics portal  Category

Gravitational waves are waves of the intensity of gravity that are generated by the accelerated masses of binary stars and other motions of gravitating masses, and propagate as waves outward from their source at the speed of light. They were first proposed by Oliver Heaviside in 1893 and then later by Henri Poincaré in 1905 as the gravitational equivalent of electromagnetic waves.^[1]

Gravitational waves were later predicted in 1916^[2][3] by Albert Einstein on the basis of his general theory of relativity as ripples in spacetime.^[4][5] Gravitational waves transport energy as gravitational radiation, a form of radiant energy similar to electromagnetic radiation.^[6] Newton's law of universal gravitation, part of classical mechanics, does not provide for their existence, since that law is predicated on the assumption that physical interactions propagate instantaneously (at infinite speed) – showing one of the ways the methods of Newtonian physics are unable to explain phenomena associated with relativity.

The first indirect evidence for the existence of gravitational waves came in 1974 from the observed orbital decay of the Hulse–Taylor binary pulsar, which matched the decay predicted by general relativity as energy is lost to gravitational radiation. In 1993, Russell A. Hulse and Joseph Hooton Taylor Jr. received the Nobel Prize in Physics for this discovery.

The first direct observation of gravitational waves was made in 2015, when a signal generated by the merger of two black holes was received by the LIGO gravitational wave detectors in Livingston, Louisiana, and in Hanford, Washington. The 2017 Nobel Prize in Physics was subsequently awarded to Rainer Weiss, Kip Thorne and Barry Barish for their role in the direct detection of gravitational waves.

In gravitational-wave astronomy, observations of gravitational waves are used to infer data about the sources of gravitational waves. Sources that can be studied this way include binary star systems composed of white dwarfs, neutron stars,^[7][8] and black holes; events such as supernovae; and the formation of the early universe shortly after the Big Bang.

Introduction

In Einstein's general theory of relativity, gravity is treated as a phenomenon resulting from the curvature of spacetime. This curvature is caused by the presence of mass. Generally, the more mass that is contained within a given volume of space, the greater the curvature of spacetime will be at the boundary of its volume.^[9] As objects with mass move around in spacetime, the curvature changes to reflect the changed locations of those objects. In certain circumstances, accelerating objects generate changes in this curvature which propagate outwards at the speed of light in a wave-like manner. These propagating phenomena are known as gravitational waves.

As a gravitational wave passes an observer, that observer will find spacetime distorted by the effects of strain. Distances between objects increase and decrease rhythmically as the wave passes, at a frequency equal to that of the wave. The magnitude of this effect is inversely proportional to the distance from the source.^[10]: 227

Inspiraling binary neutron stars are predicted to be a powerful source of gravitational waves as they coalesce, due to the very large acceleration of their masses as they orbit close to one another. However, due to the astronomical distances to these sources, the effects when measured on Earth are predicted to be very small, having strains of less than 1 part in 10²⁰.

Where General Relativity is accepted, gravitational waves as detected are attributed to ripples in spacetime; otherwise the gravitational waves can be thought of simply as a product of the orbit of binary systems. (A binary orbit causes the binary system's geometry to change through 180 degrees and also causes the distance between each body of the binary system and the observer to change through 180 degrees causing a gravitational wave frequency of two times the orbital frequency).

Scientists continue to demonstrate the existence of these waves with continuously upgraded, highly-sensitive detectors used in joint observation runs. The most sensitive detector accomplished the task possessing a sensitivity measurement of about one part in 5×10²² (as of 2012) provided by the LIGO and VIRGO observatories.^[11] In 2019, the Japanese detector KAGRA was completed and made its first joint detection with LIGO and VIRGO in 2021.^[12] A space based observatory, the Laser Interferometer Space Antenna, is currently under development by ESA. Another European ground based detector, the Einstein Telescope, is also being developed.

Linearly polarised gravitational wave

Gravitational waves can penetrate regions of space that electromagnetic waves cannot. They allow the observation of the merger of black holes and possibly other exotic objects in the distant Universe. Such systems cannot be observed with more traditional means such as optical telescopes or radio telescopes, and so gravitational wave astronomy gives new insights into the working of the Universe.

In particular, gravitational waves could be of interest to cosmologists as they offer a possible way of observing the very early Universe. This is not possible with conventional astronomy, since before recombination the Universe was opaque to electromagnetic radiation.^[13] Precise measurements of gravitational waves will also allow scientists to test more thoroughly the general theory of relativity.

In principle, gravitational waves could exist at any frequency. Very low frequency waves are detected using pulsar timing arrays. Astronomers monitor the timing of approximately 100 pulsars spread widely across our galaxy over the course of years. Pulsars are the most accurate time clocks imaginable and subtle changes in the arrival of their signals caused by passing gravity waves generated by merging Super Massive Black Holes with wavelengths measured in lightyears and then using serious computing power to decipher the source. Using this technique they have discovered the ‘hum’ of various SMBH mergers occurring in the universe. Stephen Hawking and Werner Israel list different frequency bands for gravitational waves that could plausibly be detected, ranging from 10⁻⁷ Hz up to 10¹¹ Hz.^[14]

Speed of gravity

The speed of gravitational waves in the general theory of relativity is equal to the speed of light in vacuum, c.^[15] Within the theory of special relativity, the constant c is not only about light; instead it is the highest possible speed for any interaction in nature. Formally, c is a conversion factor for changing the unit of time to the unit of space.^[16] This makes it the only speed which does not depend either on the motion of an observer or a source of light and/or gravity.

Thus, the speed of "light" is also the speed of gravitational waves, and further the speed of any massless particle. Such particles include the gluon (carrier of the strong force), the photons that make up light (hence carrier of electromagnetic force), and the hypothetical gravitons (which are the presumptive field particles associated with gravity; however, an understanding of the graviton, if any exist, requires an as-yet unavailable theory of quantum gravity).

In August 2017, the LIGO and Virgo detectors received gravitational wave signals within 2 seconds of gamma ray satellites and optical telescopes seeing signals from the same direction. This confirmed that the speed of gravitational waves was the same as the speed of light.^[17]

History

Primordial gravitational waves are hypothesized to arise from cosmic inflation, a phase of accelerated expansion just after the Big Bang (2014).^[18][19][20]

The possibility of gravitational waves and that those might travel at the speed of light was discussed in 1893 by Oliver Heaviside, using the analogy between the inverse-square law of gravitation and the electrostatic force.^[21] In 1905, Henri Poincaré proposed gravitational waves, emanating from a body and propagating at the speed of light, as being required by the Lorentz transformations^[22] and suggested that, in analogy to an accelerating electrical charge producing electromagnetic waves, accelerated masses in a relativistic field theory of gravity should produce gravitational waves.^[23][24] When Einstein published his general theory of relativity in 1915, he was skeptical of Poincaré's idea since the theory implied there were no "gravitational dipoles". Nonetheless, he still pursued the idea and based on various approximations came to the conclusion there must, in fact, be three types of gravitational waves (dubbed longitudinal–longitudinal, transverse–longitudinal, and transverse–transverse by Hermann Weyl).^[24]

However, the nature of Einstein's approximations led many (including Einstein himself) to doubt the result. In 1922, Arthur Eddington showed that two of Einstein's types of waves were artifacts of the coordinate system he used, and could be made to propagate at any speed by choosing appropriate coordinates, leading Eddington to jest that they "propagate at the speed of thought".^[25]: 72 This also cast doubt on the physicality of the third (transverse–transverse) type that Eddington showed always propagate at the speed of light regardless of coordinate system. In 1936, Einstein and Nathan Rosen submitted a paper to Physical Review in which they claimed gravitational waves could not exist in the full general theory of relativity because any such solution of the field equations would have a singularity. The journal sent their manuscript to be reviewed by Howard P. Robertson, who anonymously reported that the singularities in question were simply the harmless coordinate singularities of the employed cylindrical coordinates. Einstein, who was unfamiliar with the concept of peer review, angrily withdrew the manuscript, never to publish in Physical Review again. Nonetheless, his assistant Leopold Infeld, who had been in contact with Robertson, convinced Einstein that the criticism was correct, and the paper was rewritten with the opposite conclusion and published elsewhere.^{[24][25]: 79ff} In 1956, Felix Pirani remedied the confusion caused by the use of various coordinate systems by rephrasing the gravitational waves in terms of the manifestly observable Riemann curvature tensor.^[26]

At the time, Pirani's work was overshadowed by the community's focus on a different question: whether gravitational waves could transmit energy. This matter was settled by a thought experiment proposed by Richard Feynman during the first "GR" conference at Chapel Hill in 1957. In short, his argument known as the "sticky bead argument" notes that if one takes a rod with beads then the effect of a passing gravitational wave would be to move the beads along the rod; friction would then produce heat, implying that the passing wave had done work. Shortly after, Hermann Bondi published a detailed version of the "sticky bead argument".^[24] This later led to a series of articles (1959 to 1989) by Bondi and Pirani that established the existence of plane wave solutions for gravitational waves.^[27]

Paul Dirac further postulated the existence of gravitational waves, declaring them to have "physical significance" in his 1959 lecture at the Lindau Meetings.^[28] Further, it was Dirac who predicted gravitational waves with a well defined energy density in 1964.^[29]

After the Chapel Hill conference, Joseph Weber started designing and building the first gravitational wave detectors now known as Weber bars. In 1969, Weber claimed to have detected the first gravitational waves, and by 1970 he was "detecting" signals regularly from the Galactic Center; however, the frequency of detection soon raised doubts on the validity of his observations as the implied rate of energy loss of the Milky Way would drain our galaxy of energy on a timescale much shorter than its inferred age. These doubts were strengthened when, by the mid-1970s, repeated experiments from other groups building their own Weber bars across the globe failed to find any signals, and by the late 1970s consensus was that Weber's results were spurious.^[24]

In the same period, the first indirect evidence of gravitational waves was discovered. In 1974, Russell Alan Hulse and Joseph Hooton Taylor, Jr. discovered the first binary pulsar, which earned them the 1993 Nobel Prize in Physics.^[30] Pulsar timing observations over the next decade showed a gradual decay of the orbital period of the Hulse–Taylor pulsar that matched the loss of energy and angular momentum in gravitational radiation predicted by general relativity.^[31][32][24]

This indirect detection of gravitational waves motivated further searches, despite Weber's discredited result. Some groups continued to improve Weber's original concept, while others pursued the detection of gravitational waves using laser interferometers. The idea of using a laser interferometer for this seems to have been floated independently by various people, including M. E. Gertsenshtein and V. I. Pustovoit in 1962,^[33] and Vladimir B. Braginskiĭ in 1966. The first prototypes were developed in the 1970s by Robert L. Forward and Rainer Weiss.^[34][35] In the decades that followed, ever more sensitive instruments were constructed, culminating in the construction of GEO600, LIGO, and Virgo.^[24]

After years of producing null results, improved detectors became operational in 2015. On 11 February 2016, the LIGO-Virgo collaborations announced the first observation of gravitational waves,^{[36][37][38][39]} from a signal (dubbed GW150914) detected at 09:50:45 GMT on 14 September 2015 of two black holes with masses of 29 and 36 solar masses merging about 1.3 billion light-years away. During the final fraction of a second of the merger, it released more than 50 times the power of all the stars in the observable universe combined.^[40] The signal increased in frequency from 35 to 250 Hz over 10 cycles (5 orbits) as it rose in strength for a period of 0.2 second.^[37] The mass of the new merged black hole was 62 solar masses. Energy equivalent to three solar masses was emitted as gravitational waves.^[41] The signal was seen by both LIGO detectors in Livingston and Hanford, with a time difference of 7 milliseconds due to the angle between the two detectors and the source. The signal came from the Southern Celestial Hemisphere, in the rough direction of (but much farther away than) the Magellanic Clouds.^[39] The confidence level of this being an observation of gravitational waves was 99.99994%.^[41]

A year earlier, the BICEP2 collaboration claimed that they had detected the imprint of gravitational waves in the cosmic microwave background. However, they were later forced to retract this result.^{[18][19][42][43]}

In 2017, the Nobel Prize in Physics was awarded to Rainer Weiss, Kip Thorne and Barry Barish for their role in the detection of gravitational waves.^[44][45][46]

In 2023, NANOGrav, EPTA, PPTA, and IPTA announced that they found evidence of a universal gravitational wave background.^[47] North American Nanohertz Observatory for Gravitational Waves states, that they were created over cosmological time scales by supermassive black holes, identifying the distinctive Hellings-Downs curve in 15 years of radio observations of 25 pulsars.^[48] Similar results are published by European Pulsar Timing Array, who claimed a ${\displaystyle 3\sigma }$-significance. They expect that a ${\displaystyle 5\sigma }$-significance will be achieved by 2025 by combining the measurements of several collaborations.^[49][50]

Effects of passing

The effect of a plus-polarized gravitational wave on a ring of particles

The effect of a cross-polarized gravitational wave on a ring of particles

Gravitational waves are constantly passing Earth; however, even the strongest have a minuscule effect and their sources are generally at a great distance. For example, the waves given off by the cataclysmic final merger of GW150914 reached Earth after travelling over a billion light-years, as a ripple in spacetime that changed the length of a 4 km LIGO arm by a thousandth of the width of a proton, proportionally equivalent to changing the distance to the nearest star outside the Solar System by one hair's width.^[51] This tiny effect from even extreme gravitational waves makes them observable on Earth only with the most sophisticated detectors.

The effects of a passing gravitational wave, in an extremely exaggerated form, can be visualized by imagining a perfectly flat region of spacetime with a group of motionless test particles lying in a plane, e.g., the surface of a computer screen. As a gravitational wave passes through the particles along a line perpendicular to the plane of the particles, i.e., following the observer's line of vision into the screen, the particles will follow the distortion in spacetime, oscillating in a "cruciform" manner, as shown in the animations. The area enclosed by the test particles does not change and there is no motion along the direction of propagation.

The oscillations depicted in the animation are exaggerated for the purpose of discussion – in reality a gravitational wave has a very small amplitude (as formulated in linearized gravity). However, they help illustrate the kind of oscillations associated with gravitational waves as produced by a pair of masses in a circular orbit. In this case the amplitude of the gravitational wave is constant, but its plane of polarization changes or rotates at twice the orbital rate, so the time-varying gravitational wave size, or 'periodic spacetime strain', exhibits a variation as shown in the animation.^[52] If the orbit of the masses is elliptical then the gravitational wave's amplitude also varies with time according to Einstein's quadrupole formula.^[3]

As with other waves, there are a number of characteristics used to describe a gravitational wave:

• Amplitude: Usually denoted h, this is the size of the wave – the fraction of stretching or squeezing in the animation. The amplitude shown here is roughly h = 0.5 (or 50%). Gravitational waves passing through the Earth are many sextillion times weaker than this – h ≈ 10⁻²⁰.
• Frequency: Usually denoted f, this is the frequency with which the wave oscillates (1 divided by the amount of time between two successive maximum stretches or squeezes)
• Wavelength: Usually denoted λ, this is the distance along the wave between points of maximum stretch or squeeze.
• Speed: This is the speed at which a point on the wave (for example, a point of maximum stretch or squeeze) travels. For gravitational waves with small amplitudes, this wave speed is equal to the speed of light (c).

The speed, wavelength, and frequency of a gravitational wave are related by the equation c = λf, just like the equation for a light wave. For example, the animations shown here oscillate roughly once every two seconds. This would correspond to a frequency of 0.5 Hz, and a wavelength of about 600 000 km, or 47 times the diameter of the Earth.

In the above example, it is assumed that the wave is linearly polarized with a "plus" polarization, written h₊. Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are 45 degrees apart, as opposed to 90 degrees.^[53] In particular, in a "cross"-polarized gravitational wave, h_×, the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarized waves. Gravitational waves are polarized because of the nature of their source.

Sources

The gravitational wave spectrum with sources and detectors. Credit: NASA Goddard Space Flight Center^[54]

In general terms, gravitational waves are radiated by objects whose motion involves acceleration and its change, provided that the motion is not perfectly spherically symmetric (like an expanding or contracting sphere) or rotationally symmetric (like a spinning disk or sphere). A simple example of this principle is a spinning dumbbell. If the dumbbell spins around its axis of symmetry, it will not radiate gravitational waves; if it tumbles end over end, as in the case of two planets orbiting each other, it will radiate gravitational waves. The heavier the dumbbell, and the faster it tumbles, the greater is the gravitational radiation it will give off. In an extreme case, such as when the two weights of the dumbbell are massive stars like neutron stars or black holes, orbiting each other quickly, then significant amounts of gravitational radiation would be given off.

Some more detailed examples:

• Two objects orbiting each other, as a planet would orbit the Sun, will radiate.
• A spinning non-axisymmetric planetoid – say with a large bump or dimple on the equator – will radiate.
• A supernova will radiate except in the unlikely event that the explosion is perfectly symmetric.
• An isolated non-spinning solid object moving at a constant velocity will not radiate. This can be regarded as a consequence of the principle of conservation of linear momentum.
• A spinning disk will not radiate. This can be regarded as a consequence of the principle of conservation of angular momentum. However, it will show gravitomagnetic effects.
• A spherically pulsating spherical star (non-zero monopole moment or mass, but zero quadrupole moment) will not radiate, in agreement with Birkhoff's theorem.

More technically, the second time derivative of the quadrupole moment (or the l-th time derivative of the l-th multipole moment) of an isolated system's stress–energy tensor must be non-zero in order for it to emit gravitational radiation. This is analogous to the changing dipole moment of charge or current that is necessary for the emission of electromagnetic radiation.

Binaries

See also: Two-body problem in general relativity

Two stars of dissimilar mass are in circular orbits. Each revolves about their common center of mass (denoted by the small red cross) in a circle with the larger mass having the smaller orbit.

Two stars of similar mass in circular orbits about their center of mass

Two stars of similar mass in highly elliptical orbits about their center of mass

Gravitational waves carry energy away from their sources and, in the case of orbiting bodies, this is associated with an in-spiral or decrease in orbit.^[55][56] Imagine for example a simple system of two masses – such as the Earth–Sun system – moving slowly compared to the speed of light in circular orbits. Assume that these two masses orbit each other in a circular orbit in the x–y plane. To a good approximation, the masses follow simple Keplerian orbits. However, such an orbit represents a changing quadrupole moment. That is, the system will give off gravitational waves.

In theory, the loss of energy through gravitational radiation could eventually drop the Earth into the Sun. However, the total energy of the Earth orbiting the Sun (kinetic energy + gravitational potential energy) is about 1.14×10³⁶ joules of which only 200 watts (joules per second) is lost through gravitational radiation, leading to a decay in the orbit by about 1×10⁻¹⁵ meters per day or roughly the diameter of a proton. At this rate, it would take the Earth approximately 3×10¹³ times more than the current age of the universe to spiral onto the Sun. This estimate overlooks the decrease in r over time, but the radius varies only slowly for most of the time and plunges at later stages, as ${\displaystyle r(t)=r_{0}\left(1-{\frac {t}{t_{\text{coalesce}}}}\right)^{1/4},}$ with ${\displaystyle r_{0}}$ the initial radius and ${\displaystyle t_{\text{coalesce}}}$ the total time needed to fully coalesce.^[57]

More generally, the rate of orbital decay can be approximated by^[58]

${\displaystyle {\frac {\mathrm {d} r}{\mathrm {d} t}}=-{\frac {64}{5}}\,{\frac {G^{3}}{c^{5}}}\,{\frac {(m_{1}m_{2})(m_{1}+m_{2})}{r^{3}}}\ ,}$

where r is the separation between the bodies, t time, G the gravitational constant, c the speed of light, and m₁ and m₂ the masses of the bodies. This leads to an expected time to merger of ^[58]

${\displaystyle t={\frac {5}{256}}\,{\frac {c^{5}}{G^{3}}}\,{\frac {r^{4}}{(m_{1}m_{2})(m_{1}+m_{2})}}.}$

Compact binaries

Compact stars like white dwarfs and neutron stars can be constituents of binaries. For example, a pair of solar mass neutron stars in a circular orbit at a separation of 1.89×10⁸ m (189,000 km) has an orbital period of 1,000 seconds, and an expected lifetime of 1.30×10¹³ seconds or about 414,000 years. Such a system could be observed by LISA if it were not too far away. A far greater number of white dwarf binaries exist with orbital periods in this range. White dwarf binaries have masses in the order of the Sun, and diameters in the order of the Earth. They cannot get much closer together than 10,000 km before they will merge and explode in a supernova which would also end the emission of gravitational waves. Until then, their gravitational radiation would be comparable to that of a neutron star binary.

Artist's impression of merging neutron stars, a source of gravitational waves^[59]

When the orbit of a neutron star binary has decayed to 1.89×10⁶ m (1890 km), its remaining lifetime is about 130,000 seconds or 36 hours. The orbital frequency will vary from 1 orbit per second at the start, to 918 orbits per second when the orbit has shrunk to 20 km at merger. The majority of gravitational radiation emitted will be at twice the orbital frequency. Just before merger, the inspiral could be observed by LIGO if such a binary were close enough. LIGO has only a few minutes to observe this merger out of a total orbital lifetime that may have been billions of years. In August 2017, LIGO and Virgo observed the first binary neutron star inspiral in GW170817, and 70 observatories collaborated to detect the electromagnetic counterpart, a kilonova in the galaxy NGC 4993, 40 megaparsecs away, emitting a short gamma ray burst (GRB 170817A) seconds after the merger, followed by a longer optical transient (AT 2017gfo) powered by r-process nuclei. Advanced LIGO detectors should be able to detect such events up to 200 megaparsecs away. Within this range of the order 40 events are expected per year.^[60]

Properties and behaviour

Gravitational wave astronomy

Two-dimensional representation of gravitational waves generated by two neutron stars orbiting each other.

During the past century, astronomy has been revolutionized by the use of new methods for observing the universe. Astronomical observations were initially made using visible light. Galileo Galilei pioneered the use of telescopes to enhance these observations. However, visible light is only a small portion of the electromagnetic spectrum, and not all objects in the distant universe shine strongly in this particular band. More information may be found, for example, in radio wavelengths. Using radio telescopes, astronomers have discovered pulsars and quasars, for example. Observations in the microwave band led to the detection of faint imprints of the Big Bang, a discovery Stephen Hawking called the "greatest discovery of the century, if not all time". Similar advances in observations using gamma rays, x-rays, ultraviolet light, and infrared light have also brought new insights to astronomy. As each of these regions of the spectrum has opened, new discoveries have been made that could not have been made otherwise. The astronomy community hopes that the same holds true of gravitational waves.^[74][75]

Gravitational waves have two important and unique properties. First, there is no need for any type of matter to be present nearby in order for the waves to be generated by a binary system of uncharged black holes, which would emit no electromagnetic radiation. Second, gravitational waves can pass through any intervening matter without being scattered significantly. Whereas light from distant stars may be blocked out by interstellar dust, for example, gravitational waves will pass through essentially unimpeded. These two features allow gravitational waves to carry information about astronomical phenomena heretofore never observed by humans.^[72]

The sources of gravitational waves described above are in the low-frequency end of the gravitational-wave spectrum (10⁻⁷ to 10⁵ Hz). An astrophysical source at the high-frequency end of the gravitational-wave spectrum (above 10⁵ Hz and probably 10¹⁰ Hz) generates relic gravitational waves that are theorized to be faint imprints of the Big Bang like the cosmic microwave background.^[76] At these high frequencies it is potentially possible that the sources may be "man made"^[14] that is, gravitational waves generated and detected in the laboratory.^[77][78]

A supermassive black hole, created from the merger of the black holes at the center of two merging galaxies detected by the Hubble Space Telescope, is theorized to have been ejected from the merger center by gravitational waves.^[79][80]

Detection

Now disproved evidence allegedly showing gravitational waves in the infant universe was found by the BICEP2 radio telescope. The microscopic examination of the focal plane of the BICEP2 detector is shown here.^[18][19] In January 2015, however, the BICEP2 findings were confirmed to be the result of cosmic dust.^[81]

Ground-based detectors

A schematic diagram of a laser interferometer

Though the Hulse–Taylor observations were very important, they give only indirect evidence for gravitational waves. A more conclusive observation would be a direct measurement of the effect of a passing gravitational wave, which could also provide more information about the system that generated it. Any such direct detection is complicated by the extraordinarily small effect the waves would produce on a detector. The amplitude of a spherical wave will fall off as the inverse of the distance from the source (the 1/R term in the formulas for h above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitudes by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10⁻²⁰, but generally no bigger.^[91]

Resonant antennas

Main article: Weber bar

A simple device theorised to detect the expected wave motion is called a Weber bar – a large, solid bar of metal isolated from outside vibrations. This type of instrument was the first type of gravitational wave detector. Strains in space due to an incident gravitational wave excite the bar's resonant frequency and could thus be amplified to detectable levels. Conceivably, a nearby supernova might be strong enough to be seen without resonant amplification. With this instrument, Joseph Weber claimed to have detected daily signals of gravitational waves. His results, however, were contested in 1974 by physicists Richard Garwin and David Douglass. Modern forms of the Weber bar are still operated, cryogenically cooled, with superconducting quantum interference devices to detect vibration. Weber bars are not sensitive enough to detect anything but extremely powerful gravitational waves.^[92]

MiniGRAIL is a spherical gravitational wave antenna using this principle. It is based at Leiden University, consisting of an exactingly machined 1,150 kg sphere cryogenically cooled to 20 millikelvins.^[93] The spherical configuration allows for equal sensitivity in all directions, and is somewhat experimentally simpler than larger linear devices requiring high vacuum. Events are detected by measuring deformation of the detector sphere. MiniGRAIL is highly sensitive in the 2–4 kHz range, suitable for detecting gravitational waves from rotating neutron star instabilities or small black hole mergers.^[94]

There are currently two detectors focused on the higher end of the gravitational wave spectrum (10⁻⁷ to 10⁵ Hz): one at University of Birmingham, England,^[95] and the other at INFN Genoa, Italy. A third is under development at Chongqing University, China. The Birmingham detector measures changes in the polarization state of a microwave beam circulating in a closed loop about one meter across. Both detectors are expected to be sensitive to periodic spacetime strains of h ~ 2×10⁻¹³ /√Hz, given as an amplitude spectral density. The INFN Genoa detector is a resonant antenna consisting of two coupled spherical superconducting harmonic oscillators a few centimeters in diameter. The oscillators are designed to have (when uncoupled) almost equal resonant frequencies. The system is currently expected to have a sensitivity to periodic spacetime strains of h ~ 2×10⁻¹⁷ /√Hz, with an expectation to reach a sensitivity of h ~ 2×10⁻²⁰ /√Hz. The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ≈10¹¹ Hz (100 GHz) and h ≈10⁻³⁰ to 10⁻³².^[96]

Interferometers

Simplified operation of a gravitational wave observatory

Figure 1: A beamsplitter (green line) splits coherent light (from the white box) into two beams which reflect off the mirrors (cyan oblongs); only one outgoing and reflected beam in each arm is shown, and separated for clarity. The reflected beams recombine and an interference pattern is detected (purple circle).

Figure 2: A gravitational wave passing over the left arm (yellow) changes its length and thus the interference pattern.

A more sensitive class of detector uses a laser Michelson interferometer to measure gravitational-wave induced motion between separated 'free' masses.^[97] This allows the masses to be separated by large distances (increasing the signal size); a further advantage is that it is sensitive to a wide range of frequencies (not just those near a resonance as is the case for Weber bars). After years of development the first ground-based interferometers became operational in 2015. Currently, the most sensitive is LIGO – the Laser Interferometer Gravitational Wave Observatory. LIGO has three detectors: one in Livingston, Louisiana, one at the Hanford site in Richland, Washington and a third (formerly installed as a second detector at Hanford) that is planned to be moved to India. Each observatory has two light storage arms that are 4 kilometers in length. These are at 90 degree angles to each other, with the light passing through 1 m diameter vacuum tubes running the entire 4 kilometers. A passing gravitational wave will slightly stretch one arm as it shortens the other. This is precisely the motion to which an interferometer is most sensitive.

Even with such long arms, the strongest gravitational waves will only change the distance between the ends of the arms by at most roughly 10⁻¹⁸ m. LIGO should be able to detect gravitational waves as small as h ~ 5×10⁻²². Upgrades to LIGO and Virgo should increase the sensitivity still further. Another highly sensitive interferometer, KAGRA, which is located in the Kamioka Observatory in Japan, is in operation since February 2020. A key point is that a tenfold increase in sensitivity (radius of 'reach') increases the volume of space accessible to the instrument by one thousand times. This increases the rate at which detectable signals might be seen from one per tens of years of observation, to tens per year.^[98]

Interferometric detectors are limited at high frequencies by shot noise, which occurs because the lasers produce photons randomly; one analogy is to rainfall – the rate of rainfall, like the laser intensity, is measurable, but the raindrops, like photons, fall at random times, causing fluctuations around the average value. This leads to noise at the output of the detector, much like radio static. In addition, for sufficiently high laser power, the random momentum transferred to the test masses by the laser photons shakes the mirrors, masking signals of low frequencies. Thermal noise (e.g., Brownian motion) is another limit to sensitivity. In addition to these 'stationary' (constant) noise sources, all ground-based detectors are also limited at low frequencies by seismic noise and other forms of environmental vibration, and other 'non-stationary' noise sources; creaks in mechanical structures, lightning or other large electrical disturbances, etc. may also create noise masking an event or may even imitate an event. All of these must be taken into account and excluded by analysis before detection may be considered a true gravitational wave event.

Einstein@Home

Main article: Einstein@Home

The simplest gravitational waves are those with constant frequency. The waves given off by a spinning, non-axisymmetric neutron star would be approximately monochromatic: a pure tone in acoustics. Unlike signals from supernovae or binary black holes, these signals evolve little in amplitude or frequency over the period it would be observed by ground-based detectors. However, there would be some change in the measured signal, because of Doppler shifting caused by the motion of the Earth. Despite the signals being simple, detection is extremely computationally expensive, because of the long stretches of data that must be analysed.

The Einstein@Home project is a distributed computing project similar to SETI@home intended to detect this type of gravitational wave. By taking data from LIGO and GEO, and sending it out in little pieces to thousands of volunteers for parallel analysis on their home computers, Einstein@Home can sift through the data far more quickly than would be possible otherwise.^[99]

Using pulsar timing arrays

Main article: Pulsar timing array

Plot of correlation between pulsars observed by NANOGrav vs angular separation between pulsars, compared with a theoretical Hellings-Downs model (dashed purple) and if there were no gravitational wave background (solid green)^[100][101]

Pulsars are rapidly rotating stars. A pulsar emits beams of radio waves that, like lighthouse beams, sweep through the sky as the pulsar rotates. The signal from a pulsar can be detected by radio telescopes as a series of regularly spaced pulses, essentially like the ticks of a clock. GWs affect the time it takes the pulses to travel from the pulsar to a telescope on Earth. A pulsar timing array uses millisecond pulsars to seek out perturbations due to GWs in measurements of the time of arrival of pulses to a telescope, in other words, to look for deviations in the clock ticks. To detect GWs, pulsar timing arrays search for a distinct quadrupolar pattern of correlation and anti-correlation between the time of arrival of pulses from different pulsar pairs as a function of their angular separation in the sky.^[102] Although pulsar pulses travel through space for hundreds or thousands of years to reach us, pulsar timing arrays are sensitive to perturbations in their travel time of much less than a millionth of a second.

The most likely source of GWs to which pulsar timing arrays are sensitive are supermassive black hole binaries, which form from the collision of galaxies.^[103] In addition to individual binary systems, pulsar timing arrays are sensitive to a stochastic background of GWs made from the sum of GWs from many galaxy mergers. Other potential signal sources include cosmic strings and the primordial background of GWs from cosmic inflation.

Globally there are three active pulsar timing array projects. The North American Nanohertz Observatory for Gravitational Waves uses data collected by the Arecibo Radio Telescope and Green Bank Telescope. The Australian Parkes Pulsar Timing Array uses data from the Parkes radio-telescope. The European Pulsar Timing Array uses data from the four largest telescopes in Europe: the Lovell Telescope, the Westerbork Synthesis Radio Telescope, the Effelsberg Telescope and the Nancay Radio Telescope. These three groups also collaborate under the title of the International Pulsar Timing Array project.^[104]

In June 2023, NANOGrav published the 15-year data release, which contained the first evidence for a stochastic gravitational wave background. In particular, it included the first measurement of the Hellings-Downs curve, the tell-tale sign of the gravitational wave origin of the observed background.^[105][106]

LIGO and Virgo observations

Main articles: First observation of gravitational waves and List of gravitational wave observations

LIGO measurement of the gravitational waves at the Hanford (left) and Livingston (right) detectors, compared to the theoretical predicted values.

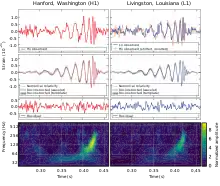
On 11 February 2016, the LIGO collaboration announced the first observation of gravitational waves, from a signal detected at 09:50:45 GMT on 14 September 2015^[36] of two black holes with masses of 29 and 36 solar masses merging about 1.3 billion light-years away. During the final fraction of a second of the merger, it released more than 50 times the power of all the stars in the observable universe combined.^[107] The signal increased in frequency from 35 to 250 Hz over 10 cycles (5 orbits) as it rose in strength for a period of 0.2 second.^[37] The mass of the new merged black hole was 62 solar masses. Energy equivalent to three solar masses was emitted as gravitational waves.^[41] The signal was seen by both LIGO detectors in Livingston and Hanford, with a time difference of 7 milliseconds due to the angle between the two detectors and the source. The signal came from the Southern Celestial Hemisphere, in the rough direction of (but much farther away than) the Magellanic Clouds.^[39] The gravitational waves were observed in the region more than 5 sigma^[108] (in other words, 99.99997% chances of showing/getting the same result), the probability of finding enough to have been assessed/considered as the evidence/proof in a experiment of statistical physics.^[109]

Since then LIGO and Virgo have reported more gravitational wave observations from merging black hole binaries.

On 16 October 2017, the LIGO and Virgo collaborations announced the first-ever detection of gravitational waves originating from the coalescence of a binary neutron star system. The observation of the GW170817 transient, which occurred on 17 August 2017, allowed for constraining the masses of the neutron stars involved between 0.86 and 2.26 solar masses. Further analysis allowed a greater restriction of the mass values to the interval 1.17–1.60 solar masses, with the total system mass measured to be 2.73–2.78 solar masses. The inclusion of the Virgo detector in the observation effort allowed for an improvement of the localization of the source by a factor of 10. This in turn facilitated the electromagnetic follow-up of the event. In contrast to the case of binary black hole mergers, binary neutron star mergers were expected to yield an electromagnetic counterpart, that is, a light signal associated with the event. A gamma-ray burst (GRB 170817A) was detected by the Fermi Gamma-ray Space Telescope, occurring 1.7 seconds after the gravitational wave transient. The signal, originating near the galaxy NGC 4993, was associated with the neutron star merger. This was corroborated by the electromagnetic follow-up of the event (AT 2017gfo), involving 70 telescopes and observatories and yielding observations over a large region of the electromagnetic spectrum which further confirmed the neutron star nature of the merged objects and the associated kilonova.^[110][111]

In 2021, the detection of the first two neutron star-black hole binaries by the LIGO and VIRGO detectors was published in the Astrophysical Journal Letters, allowing to first set bounds on the quantity of such systems. No neutron star-black hole binary had ever been observed using conventional means before the gravitational observation.^[8]

Microscopic sources

In 1964 L. Halpern and B. Laurent theoretically proved that gravitational spin-2 electron transitions are possible in atoms. Compared to electric and magnetic transitions the emission probability is extremely low. Stimulated emission was discussed for increasing the efficiency of the process. Due to the lack of mirrors or resonators for gravitational waves, they determined that a single pass GASER (a kind of laser emitting gravitational waves) is practically unfeasible.^[112]

In 1998 the possibility of a different implementation of the above theoretical analysis was proposed by Giorgio Fontana. The required coherence for a practical GASER could be obtained by cooper pairs in superconductors that are characterized by a macroscopic collective wave-function. Cuprate high temperature superconductors are characterized by the presence of s-wave and d-wave^[113] cooper pairs. Transitions between s-wave and d-wave are gravitational spin-2. Out of equilibrium conditions can be induced by injecting s-wave cooper pairs from a low temperature superconductor, for instance lead or niobium, which is pure s-wave, by means of a Josephson junction with high critical current. The amplification mechanism can be described as the effect of superradiance, and 10 cubic centimeters of cuprate high temperature superconductor seem sufficient for the mechanism to properly work. A detailed description of the approach can be found in "High Temperature Superconductors as Quantum Sources of Gravitational Waves: The HTSC GASER". Chapter 3 of this book.^[114]

In fiction

An episode of the 1962 Russian science-fiction novel Space Apprentice by Arkady and Boris Strugatsky shows the experiment monitoring the propagation of gravitational waves at the expense of annihilating a chunk of asteroid 15 Eunomia the size of Mount Everest.^[115]

In Stanislaw Lem's 1986 novel Fiasco, a "gravity gun" or "gracer" (gravity amplification by collimated emission of resonance) is used to reshape a collapsar, so that the protagonists can exploit the extreme relativistic effects and make an interstellar journey.

In Greg Egan's 1997 novel Diaspora, the analysis of a gravitational wave signal from the inspiral of a nearby binary neutron star reveals that its collision and merger is imminent, implying a large gamma-ray burst is going to impact the Earth.

In Liu Cixin's 2006 Remembrance of Earth's Past series, gravitational waves are used as an interstellar broadcast signal, which serves as a central plot point in the conflict between civilizations within the galaxy.

See also

References

Further reading

• Bartusiak, Marcia. Einstein's Unfinished Symphony. Washington, DC: Joseph Henry Press, 2000.
• Chakrabarty, Indrajit (1999). "Gravitational Waves: An Introduction". arXiv:physics/9908041.
• Landau, L. D. and Lifshitz, E. M., The Classical Theory of Fields (Pergamon Press), 1987.
• Will, Clifford M. (2014). "The Confrontation between General Relativity and Experiment". Living Reviews in Relativity. 17 (1): 4. arXiv:1403.7377. Bibcode:2014LRR....17....4W. doi:10.12942/lrr-2014-4. PMC 5255900. PMID 28179848.
• Saulson, Peter R. (1994). Fundamentals of Interferometric Gravitational Wave Detectors. World Scientific. Bibcode:1994figw.book.....S. doi:10.1142/2410. ISBN 978-981-02-1820-1.
• Barish, Barry C.; Weiss, Rainer (1999). "LIGO and the Detection of Gravitational Waves". Physics Today. 54 (10): 44. Bibcode:1999PhT....52j..44B. doi:10.1063/1.882861.

Bibliography

• Berry, Michael, Principles of Сosmology and Gravitation (Adam Hilger, Philadelphia, 1989). ISBN 0-85274-037-9
• Collins, Harry, Gravity's Shadow: The Search for Gravitational Waves, University of Chicago Press, 2004. ISBN 0-226-11378-7
• Collins, Harry, Gravity's Kiss: The Detection of Gravitational Waves (The MIT Press, Cambridge Massachusetts, 2017). ISBN 978-0-262-03618-4.
• Davies, P.C.W., The Search for Gravity Waves (Cambridge University Press, 1980). ISBN 0521231973.
• Grote, Hartmut, Gravitational Waves: A history of discovery (CRC Press, Taylor & Francis Group, Boca Raton/London/New York, 2020). ISBN 978-0-367-13681-9.
• P. J. E. Peebles, Principles of Physical Cosmology (Princeton University Press, Princeton, 1993). ISBN 0-691-01933-9.
• Wheeler, John Archibald and Ciufolini, Ignazio, Gravitation and Inertia (Princeton University Press, Princeton, 1995). ISBN 0-691-03323-4.
• Woolf, Harry, ed., Some Strangeness in the Proportion (Addison–Wesley, Reading, Massachusetts, 1980). ISBN 0-201-09924-1.

External links

Wikimedia Commons has media related to Gravitational waves.

Look up gravitational wave in Wiktionary, the free dictionary.

• Laser Interferometer Gravitational Wave Observatory. LIGO Laboratory, operated by the California Institute of Technology and the Massachusetts Institute of Technology
• Gravitational Waves – Collected articles at Nature Journal
• Gravitational Waves – Collected articles Scientific American
• Video (94:34) – Scientific Talk on Discovery, Barry Barish, CERN (11 February 2016)
• Christina Sormani; C. Denson Hill; Paweł Nurowski; Lydia Bieri; David Garfinkle; Nicolás Yunes (August 2017). "A two-part feature: The Mathematics of Gravitational waves". Notices of the American Mathematical Society. 64 (7): 684–707. doi:10.1090/noti1551. ISSN 1088-9477.