The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics.
Fibrations are used, for example, in Postnikov systems or obstruction theory.
In this article, all mappings are continuous mappings between topological spaces.
Formal definitions
Homotopy lifting property
A mapping satisfies the homotopy lifting property for a space if:
- for every homotopy and
- for every mapping (also called lift) lifting (i.e. )
there exists a (not necessarily unique) homotopy lifting (i.e. ) with
The following commutative diagram shows the situation: [1]: 66
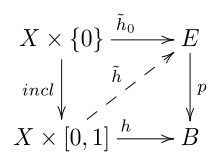
Fibration
A fibration (also called Hurewicz fibration) is a mapping satisfying the homotopy lifting property for all spaces The space is called base space and the space is called total space. The fiber over is the subspace [1]: 66
Serre fibration
A Serre fibration (also called weak fibration) is a mapping satisfying the homotopy lifting property for all CW-complexes.[2]: 375-376
Every Hurewicz fibration is a Serre fibration.
Quasifibration
A mapping is called quasifibration, if for every and holds that the induced mapping is an isomorphism.
Every Serre fibration is a quasifibration.[3]: 241-242
Examples
- The projection onto the first factor is a fibration. That is, trivial bundles are fibrations.
- Every covering is a fibration. Specifically, for every homotopy and every lift there exists a uniquely defined lift with [4]: 159 [5]: 50
- Every fiber bundle satisfies the homotopy lifting property for every CW-complex.[2]: 379
- A fiber bundle with a paracompact and Hausdorff base space satisfies the homotopy lifting property for all spaces.[2]: 379
- An example for a fibration, which is not a fiber bundle, is given by the mapping induced by the inclusion where a topological space and is the space of all continuous mappings with the compact-open topology.[4]: 198
- The Hopf fibration is a non trivial fiber bundle and specifically a Serre fibration.
Basic concepts
Fiber homotopy equivalence
A mapping between total spaces of two fibrations and with the same base space is a fibration homomorphism if the following diagram commutes:

The mapping is a fiber homotopy equivalence if in addition a fibration homomorphism exists, such that the mappings and are homotopic, by fibration homomorphisms, to the identities and [2]: 405-406
Pullback fibration
Given a fibration and a mapping , the mapping is a fibration, where is the pullback and the projections of onto and yield the following commutative diagram:
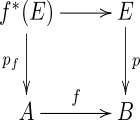
The fibration is called the pullback fibration or induced fibration.[2]: 405-406
Pathspace fibration
With the pathspace construction, any continuous mapping can be extended to a fibration by enlarging its domain to a homotopy equivalent space. This fibration is called pathspace fibration.
The total space of the pathspace fibration for a continuous mapping between topological spaces consists of pairs with and paths with starting point where is the unit interval. The space carries the subspace topology of where describes the space of all mappings and carries the compact-open topology.
The pathspace fibration is given by the mapping with The fiber is also called the homotopy fiber of and consists of the pairs with and paths where and holds.
For the special case of the inclusion of the base point , an important example of the pathspace fibration emerges. The total space consists of all paths in which starts at This space is denoted by and is called path space. The pathspace fibration maps each path to its endpoint, hence the fiber consists of all closed paths. The fiber is denoted by and is called loop space.[2]: 407-408
Properties
- The fibers over are homotopy equivalent for each path component of [2]: 405
- For a homotopy the pullback fibrations and are fiber homotopy equivalent.[2]: 406
- If the base space is contractible, then the fibration is fiber homotopy equivalent to the product fibration [2]: 406
- The pathspace fibration of a fibration is very similar to itself. More precisely, the inclusion is a fiber homotopy equivalence.[2]: 408
- For a fibration with fiber and contractible total space, there is a weak homotopy equivalence [2]: 408
Puppe sequence
For a fibration with fiber and base point the inclusion of the fiber into the homotopy fiber is a homotopy equivalence. The mapping with , where and is a path from to in the base space, is a fibration. Specifically it is the pullback fibration of the pathspace fibration . This procedure can now be applied again to the fibration and so on. This leads to a long sequence:
The fiber of over a point consists of the pairs with closed paths and starting point , i.e. the loop space . The inclusion is a homotopy equivalence and iteration yields the sequence:
Due to the duality of fibration and cofibration, there also exists a sequence of cofibrations. These two sequences are known as the Puppe sequences or the sequences of fibrations and cofibrations.[2]: 407-409
Principal fibration
A fibration with fiber is called principal, if there exists a commutative diagram:
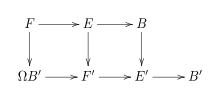
The bottom row is a sequence of fibrations and the vertical mappings are weak homotopy equivalences. Principal fibrations play an important role in Postnikov towers.[2]: 412
Long exact sequence of homotopy groups
For a Serre fibration there exists a long exact sequence of homotopy groups. For base points and this is given by:
The homomorphisms and are the induced homomorphisms of the inclusion and the projection [2]: 376
Hopf fibration
Hopf fibrations are a family of fiber bundles whose fiber, total space and base space are spheres:
The long exact sequence of homotopy groups of the hopf fibration yields:
This sequence splits into short exact sequences, as the fiber in is contractible to a point:
This short exact sequence splits because of the suspension homomorphism and there are isomorphisms:
The homotopy groups are trivial for so there exist isomorphisms between and for
Analog the fibers in and in are contractible to a point. Further the short exact sequences split and there are families of isomorphisms:[6]: 111
and
Spectral sequence
Spectral sequences are important tools in algebraic topology for computing (co-)homology groups.
The Leray-Serre spectral sequence connects the (co-)homology of the total space and the fiber with the (co-)homology of the base space of a fibration. For a fibration with fiber where the base space is a path connected CW-complex, and an additive homology theory there exists a spectral sequence:[7]: 242
Fibrations do not yield long exact sequences in homology, as they do in homotopy. But under certain conditions, fibrations provide exact sequences in homology. For a fibration with fiber where base space and fiber are path connected, the fundamental group acts trivially on and in addition the conditions for and for hold, an exact sequence exists (also known under the name Serre exact sequence):
[7]: 250
This sequence can be used, for example, to prove Hurewicz's theorem or to compute the homology of loopspaces of the form [8]: 162
For the special case of a fibration where the base space is a -sphere with fiber there exist exact sequences (also called Wang sequences) for homology and cohomology:[1]: 456
Orientability
For a fibration with fiber and a fixed commuative ring with a unit, there exists a contravariant functor from the fundamental groupoid of to the category of graded -modules, which assigns to the module and to the path class the homomorphism where is a homotopy class in
A fibration is called orientable over if for any closed path in the following holds: [1]: 476
Euler characteristic
For an orientable fibration over the field with fiber and path connected base space, the Euler characteristic of the total space is given by:
Here the Euler characteristics of the base space and the fiber are defined over the field .[1]: 481
See also
References
- 1 2 3 4 5 Spanier, Edwin H. (1966). Algebraic Topology. McGraw-Hill Book Company. ISBN 978-0-387-90646-1.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Hatcher, Allen (2001). Algebraic Topology. NY: Cambridge University Press. ISBN 0-521-79160-X.
- ↑ Dold, Albrecht; Thom, René (1958). "Quasifaserungen und Unendliche Symmetrische Produkte". Annals of Mathematics. 67 (2): 239–281. doi:10.2307/1970005. JSTOR 1970005.
- 1 2 Laures, Gerd; Szymik, Markus (2014). Grundkurs Topologie (in German) (2nd ed.). Springer Spektrum. doi:10.1007/978-3-662-45953-9. ISBN 978-3-662-45952-2.
- ↑ May, J.P. (1999). A Concise Course in Algebraic Topology (PDF). University of Chicago Press. ISBN 0-226-51182-0. OCLC 41266205.
- ↑ Steenrod, Norman (1951). The Topology of Fibre Bundles. Princeton University Press. ISBN 0-691-08055-0.
- 1 2 Davis, James F.; Kirk, Paul (1991). Lecture Notes in Algebraic Topology (PDF). Department of Mathematics, Indiana University.
- ↑ Cohen, Ralph L. (1998). The Topology of Fiber Bundles Lecture Notes (PDF). Stanford University.