Electron diffraction is a generic term for phenomena associated with changes in the direction of electron beams due to elastic interactions with atoms.[lower-alpha 1] It occurs due to elastic scattering, when there is no change in the energy of the electrons.[1]: Chpt 4 [2]: Chpt 5 [3][4] The negatively charged electrons are scattered due to Coulomb forces when they interact with both the positively charged atomic core and the negatively charged electrons around the atoms. The resulting map of the directions of the electrons far from the sample is called a diffraction pattern, see for instance Figure 1. Beyond patterns showing the directions of electrons, electron diffraction also plays a major role in the contrast of images in electron microscopes.
This article provides an overview of electron diffraction and electron diffraction patterns, collective referred to by the generic name electron diffraction. This includes aspects of how in a general way electrons can act as waves, and diffract and interact with matter. It also involves the extensive history behind modern electron diffraction, how the combination of developments in the 19th century in understanding and controlling electrons in vacuum and the early 20th century developments with electron waves were combined with early instruments, giving birth to electron microscopy and diffraction in 1920–1935. While this was the birth, there have been a large number of further developments since then.
There are many types and techniques of electron diffraction. The most common approach is where the electrons transmit through a thin sample, from 1 nm to 100 nm (10 atoms to 1000 thick), where the results depending upon how the atoms are arranged in the material, for instance a single crystal, many crystals or different types of solids. Other cases such as larger repeats, no periodicity or disorder have their own characteristic patterns. There are many different ways of collecting diffraction information, from parallel illumination to a converging beam of electrons or where the beam is rotated or scanned across the sample which produce information that is often easier to interpret. There are also many other types of instruments. For instance, in a scanning electron microscope (SEM), electron backscatter diffraction can be used to determine crystal orientation across the sample. Electron diffraction patterns can also be used to characterize molecules using gas electron diffraction, liquids, surfaces using lower energy electrons, a technique called LEED, and by reflecting electrons off surfaces, a technique called RHEED.
There are also many levels of analysis of electron diffraction, including:
- The simplest approximation using the de Broglie wavelength[5]: Chpt 1-2 for electrons, where only the geometry is considered and often Bragg's law[6]: 96–97 is invoked. This approach only considers the electrons far from the sample, a far-field or Fraunhofer[1]: 21–24 approach.
- The first level of more accuracy where it is approximated that the electrons are only scattered once, which is called kinematical diffraction[1]: Sec 2 [7]: Chpt 4-7 and is also a far-field or Fraunhofer[1]: 21–24 approach.
- More complete and accurate explanations where multiple scattering is included, what is called dynamical diffraction (e.g. refs[1]: Sec 3 [7]: Chpt 8-12 [8]: Chpt 3-10 [9][10]). These involve more general analyses using relativistically corrected Schrödinger equation[11] methods, and track the electrons through the sample, being accurate both near and far from the sample (both Fresnel and Fraunhofer diffraction).
Electron diffraction is similar to x-ray and neutron diffraction. However, unlike x-ray and neutron diffraction where the simplest approximations are quite accurate, with electron diffraction this is not the case.[1]: Sec 3 [2]: Chpt 5 Simple models give the geometry of the intensities in a diffraction pattern, but dynamical diffraction approaches are needed for accurate intensities and the positions of diffraction spots.
A primer on electron diffraction
All matter can be thought of as matter waves,[5]: Chpt 1-3 from small particles such as electrons up to macroscopic objects – although it is impossible to measure any of the "wave-like" behavior of macroscopic objects. Waves can move around objects and create interference patterns,[12]: Chpt 7-8 and a classic example is the Young's two-slit experiment shown in Figure 2, where a wave impinges upon two slits in the first of the two images (blue waves). After going through the slits there are directions where the wave is stronger, ones where it is weaker – the wave has been diffracted.[12]: Chpt 1,7,8 If instead of two slits there are a number of small points then similar phenomena can occur as shown in the second image where the wave (red and blue) is coming in from the bottom right corner. This is comparable to diffraction of an electron wave where the small dots would be atoms in a small crystal, see also note.[lower-alpha 1] Note the strong dependence on the relative orientation of the crystal and the incoming wave.
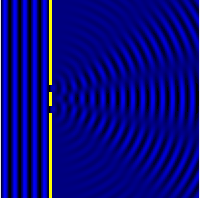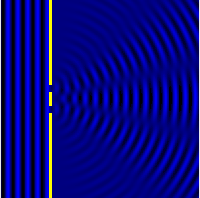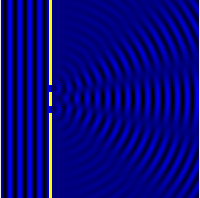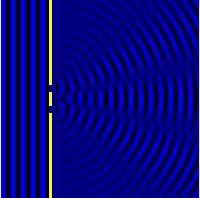

Close to an aperture or atoms, often called the "sample", the electron wave would be described in terms of near field or Fresnel diffraction.[12]: Chpt 7-8 This has relevance for imaging within electron microscopes,[1]: Chpt 3 [2]: Chpt 3-4 whereas electron diffraction patterns are measured far from the sample, which is described as far-field or Fraunhofer diffraction.[12]: Chpt 7-8 A map of the directions of the electron waves leaving the sample will show high intensity (white) for favored directions, such as the three prominent ones in the Young's two-slit experiment of Figure 2, while the other directions will be low intensity (dark). Often there will be an array of spots (preferred directions) as in Figure 1 and the other figures shown later.
History
The historical background is divided into several subsections. The first is the general background to electrons in vacuum and the technological developments that led to cathode-ray tubes as well as vacuum tubes that dominated early television and electronics; the second is how these led to the development of electron microscopes; the last is work on the nature of electron beams and the fundamentals of how electrons behave, a key component of quantum mechanics and the explanation of electron diffraction.
Electrons in vacuum
.jpg.webp)
.jpg.webp)
Experiments involving electron beams occurred long before the discovery of the electron; ēlektron (ἤλεκτρον) is the Greek word for amber,[13] which is connected to the recording of electrostatic charging[14] by Thales of Miletus around 585 BCE, and possibly others even earlier.[14]
In 1650, Otto von Guericke invented the vacuum pump[15] allowing for the study of the effects of high voltage electricity passing through rarefied air. In 1838, Michael Faraday applied a high voltage between two metal electrodes at either end of a glass tube that had been partially evacuated of air, and noticed a strange light arc with its beginning at the cathode (negative electrode) and its end at the anode (positive electrode).[16] Building on this, in the 1850s, Heinrich Geissler was able to achieve a pressure of around 10−3 atmospheres, inventing what became known as Geissler tubes. Using these tubes, while studying electrical conductivity in rarefied gases in 1859, Julius Plücker observed that the radiation emitted from the negatively charged cathode caused phosphorescent light to appear on the tube wall near it, and the region of the phosphorescent light could be moved by application of a magnetic field.[17]
In 1869, Plücker's student Johann Wilhelm Hittorf found that a solid body placed between the cathode and the phosphorescence would cast a shadow on the tube wall, e.g. Figure 3.[18] Hittorf inferred that there are straight rays emitted from the cathode and that the phosphorescence was caused by the rays striking the tube walls. In 1876 Eugen Goldstein showed that the rays were emitted perpendicular to the cathode surface, which differentiated them from the incandescent light. Eugen Goldstein dubbed them cathode rays.[19][20] By the 1870s William Crookes[21] and others were able to evacuate glass tubes below 10−6 atmospheres, and observed that the glow in the tube disappeared when the pressure was reduced but the glass behind the anode began to glow. Crookes was also able to show that the particles in the cathode rays were negatively charged and could be deflected by an electromagnetic field.[21][18]
In 1897, Joseph Thomson measured the mass of these cathode rays,[22] proving they were made of particles. These particles, however, were 1800 times lighter than the lightest particle known at that time – a hydrogen atom. These were originally called corpuscles and later named electrons by George Johnstone Stoney.[23]
The control of electron beams that this work led to resulted in significant technology advances in electronic amplifiers and television displays.[18]
Waves, diffraction and quantum mechanics
.gif)
Independent of the developments for electrons in vacuum, at about the same time the components of quantum mechanics were being assembled. In 1924 Louis de Broglie in his PhD thesis Recherches sur la théorie des quanta[5] introduced his theory of electron waves. He suggested that an electron around a nucleus could be thought of as standing waves,[5]: Chpt 3 and that electrons and all matter could be considered as waves. He merged the idea of thinking about them as particles (or corpuscles), and of thinking of them as waves. He proposed that particles are bundles of waves (wave packets) that move with a group velocity[5]: Chpt 1-2 and have an effective mass, see for instance Figure 4. Both of these depend upon the energy, which in turn connects to the wavevector and the relativistic formulation of Albert Einstein a few years before.[24]
This rapidly became part of what was called by Erwin Schrödinger undulatory mechanics,[11] now called the Schrödinger equation or wave mechanics. As stated by Louis de Broglie on September 8, 1927, in the preface to the German translation of his theses (in turn translated into English):[5]: v
M. Einstein from the beginning has supported my thesis, but it was M. E. Schrödinger who developed the propagation equations of a new theory and who in searching for its solutions has established what has become known as “Wave Mechanics”.
The Schrödinger equation combines the kinetic energy of waves and the potential energy due to, for electrons, the Coulomb potential. He was able to explain earlier work such as the quantization of the energy of electrons around atoms in the Bohr model,[25] as well as many other phenomena.[11] Electron waves as hypothesized[5]: Chpt 1-2 by de Broglie were automatically part of the solutions to his equation,[11] see also introduction to quantum mechanics and matter waves.
Both the wave nature and the undulatory mechanics approach were experimentally confirmed for electron beams by experiments from two groups performed independently, the first the Davisson–Germer experiment,[26][27][28][29] the other by George Paget Thomson and Alexander Reid;[30] see note[lower-alpha 2] for more discussion. Alexander Reid, who was Thomson's graduate student, performed the first experiments,[31] but he died soon after in a motorcycle accident[32] and is rarely mentioned. These experiments were rapidly followed by the first non-relativistic diffraction model for electrons by Hans Bethe[33] based upon the Schrödinger equation,[11] which is very close to how electron diffraction is now described. Significantly, Clinton Davisson and Lester Germer noticed[28][29] that their results could not be interpreted using a Bragg's law approach as the positions were systematically different; the approach of Hans Bethe[33] which includes the refraction due to the average potential yielded more accurate results. These advances in understanding of electron wave mechanics were important for many developments of electron-based analytical techniques such as Seishi Kikuchi's observations of lines due to combined elastic and inelastic scattering,[34][35] gas electron diffraction developed by Herman Mark and Raymond Weil,[36][37] diffraction in liquids by Louis Maxwell,[38] and the first electron microscopes developed by Max Knoll and Ernst Ruska.[39][40]
Electron microscopes and early electron diffraction
In order to have a practical microscope or diffractometer, just having an electron beam was not enough, it needed to be controlled. Many developments laid the groundwork of electron optics; see the paper by Chester J. Calbick for an overview of the early work.[41] One significant step was the work of Heinrich Hertz in 1883[42] who made a cathode-ray tube with electrostatic and magnetic deflection, demonstrating manipulation of the direction of an electron beam. Others were focusing of electrons by an axial magnetic field by Emil Wiechert in 1899,[43] improved oxide-coated cathodes which produced more electrons by Arthur Wehnelt in 1905[44] and the development of the electromagnetic lens in 1926 by Hans Busch.[45]

Building an electron microscope involves combining these elements, similar to an optical microscope but with magnetic or electrostatic lenses instead of glass ones. To this day the issue of who invented the transmission electron microscope is controversial, as discussed by Thomas Mulvey[46] and more recently by Yaping Tao.[47] Extensive additional information can be found in the articles by Martin Freundlich,[48] Reinhold Rüdenberg[49] and Mulvey.[46]
One effort was university based. In 1928, at the Technical University of Berlin, Adolf Matthias (Professor of High Voltage Technology and Electrical Installations) appointed Max Knoll to lead a team of researchers to advance research on electron beams and cathode-ray oscilloscopes. The team consisted of several PhD students including Ernst Ruska. In 1931, Max Knoll and Ernst Ruska[39][40] successfully generated magnified images of mesh grids placed over an anode aperture. The device, a replicate of which is shown in Figure 5, used two magnetic lenses to achieve higher magnifications, the first electron microscope. (Max Knoll died in 1969,[50] so did not receive a share of the Nobel Prize in Physics in 1986.)
Apparently independent of this effort was work at Siemens-Schuckert by Reinhold Rudenberg. According to patent law (U.S. Patent No. 2058914[51] and 2070318,[52] both filed in 1932), he is the inventor of the electron microscope, but it is not clear when he had a working instrument. He stated in a very brief article in 1932[53] that Siemens had been working on this for some years before the patents were filed in 1932, so his effort was parallel to the university effort. He died in 1961,[54] so similar to Max Knoll, was not eligible for a share of the Nobel Prize.
These instruments could produce magnified images, but were not particularly useful for electron diffraction; indeed, the wave nature of electrons was not exploited during the development. Key for electron diffraction in microscopes was the advance in 1936 where Hans Boersch showed that they could be used as micro-diffraction cameras with an aperture[55]—the birth of selected area electron diffraction.[7]: Chpt 5-6
Less controversial was the development of LEED—the early experiments of Davisson and Germer used this approach.[27][28] As early as 1929 Germer investigated gas adsorption,[56] and in 1932 Harrison E. Farnsworth probed single crystals of copper and silver.[57] However, the vacuum systems available at that time were not good enough to properly control the surfaces, and it took almost forty years before these became available.[58][59] Similarly, it was not until about 1965 that Peter B. Sewell and M. Cohen demonstrated the power of RHEED in a system with a very well controlled vacuum.[60]
Subsequent developments in methods and modelling
Despite early successes such as the determination of the positions of hydrogen atoms in NH4Cl crystals by W. E. Laschkarew and I. D. Usykin in 1933,[61] boric acid by John M. Cowley in 1953[62] and orthoboric acid by William Houlder Zachariasen in 1954,[63] electron diffraction for many years was a qualitative technique used to check samples within electron microscopes. John M Cowley explains in a 1968 paper:[64]
Thus was founded the belief, amounting in some cases almost to an article of faith, and persisting even to the present day, that it is impossible to interpret the intensities of electron diffraction patterns to gain structural information.
This has changed, in transmission, reflection and for low energies. Some of the key developments (some of which are also described later) from the early days to 2023 have been:
- Fast numerical methods based upon the Cowley-Moodie multislice algorithm,[65][66] which only became possible[67] once the fast Fourier transform (FFT) method was developed.[68] With these and other numerical methods Fourier transforms are fast,[69] and it became possible to calculate accurate, dynamical diffraction in seconds to minutes with laptops using widely available multislice programs.
- Developments in the convergent-beam electron diffraction approach. Building on the original work of Walther Kossel and Gottfried Möllenstedt in 1939,[70] it was extended by Peter Goodman and Gunter Lehmpfuhl,[71] then mainly by the groups of John Steeds[72][73][74] and Michiyoshi Tanaka[75][76] who showed how to determine point groups and space groups. It can also be used for higher-level refinements of the electron density;[77]: Chpt 4 for a brief history see CBED history. In many cases this is the best method to determine symmetry.[72][78]
- The development of new approaches to reduce dynamical effects such as precession electron diffraction and three-dimensional diffraction methods. Averaging over different directions has, empirically, been found to significantly reduce dynamical diffraction effects, e.g.,[79] see PED history for further details. Not only is it easier to identify known structures with this approach, it can also be used to solve unknown structures in some cases[80][79][81] – see precession electron diffraction for further information.
- The development of experimental methods exploiting ultra-high vacuum technologies (e.g. the approach described by Daniel J. Alpert in 1953[82]) to better control surfaces, making LEED and RHEED more reliable and reproducible techniques. In the early days the surfaces were not well controlled; with these technologies they can both be cleaned and remain clean for hours to days, a key component of surface science.[82][83]
- Fast and accurate methods to calculate intensities for LEED so it could be used to determine atomic positions, for instance references.[84][85][9] These have been extensively exploited to determine the structure of many surfaces, and the arrangement of foreign atoms on surfaces.[86]
- Methods to simulate the intensities in RHEED, so it can be used semi-quantitatively to understand surfaces during growth and thereby to control the resulting materials.[87]
- The development of advanced detectors for transmission electron microscopy such as charge-coupled device[88] and direct electron detectors,[89] which improve the accuracy and reliability of intensity measurements. These have efficiencies and accuracies that can be a thousand or more times that of the photographic film used in the earliest experiments,[88][89] with the information available in real time rather than requiring photographic processing after the experiment.[88][89]
Core elements of electron diffraction
Plane waves, wavevectors and reciprocal lattice
What is seen in an electron diffraction pattern depends upon the sample and also the energy of the electrons. The electrons need to be considered as waves, which involves describing the electron via a wavefunction, written in crystallographic notation (see notes[lower-alpha 3] and[lower-alpha 4]) as:[3]
for a position . This is a quantum mechanics description; one cannot use a classical approach. The vector is called the wavevector, has units of inverse nanometers, and the form above is called a plane wave as the term inside the exponential is constant on the surface of a plane. The vector is what is used when drawing ray diagrams,[1]: Chpt 3 and in vacuum is parallel to the direction or, better, group velocity[5]: Chpt 1-2 [90]: 16 or probability current[90]: 27, 130 of the plane wave. For most cases the electrons are travelling at a respectable fraction of the speed of light, so rigorously need to be considered using relativistic quantum mechanics via the Dirac equation,[91] which as spin does not normally matter can be reduced to the Klein–Gordon equation. Fortunately one can side-step many complications and use a non-relativistic approach based around the Schrödinger equation.[11] Following Kunio Fujiwara[92] and Archibald Howie,[93] the relationship between the total energy of the electrons and the wavevector is written as:
with
where is Planck's constant, is a relativistic effective mass used to cancel out the relativistic terms for electrons of energy with the speed of light and the rest mass of the electron. The concept of effective mass occurs throughout physics (see for instance Ashcroft and Mermin),[6]: Chpt 12 and comes up in the behavior of quasiparticles. A common one is the electron hole, which acts as if it is a particle with a positive charge and a mass similar to that of an electron, although it can be several times lighter or heavier. For electron diffraction the electrons behave as if they are non-relativistic particles of mass in terms of how they interact with the atoms.[92] The wavelength of the electrons in vacuum is from the above equations
and can range from about 0.1 nanometers, roughly the size of an atom, down to a thousandth of that. Typically the energy of the electrons is written in electronvolts (eV), the voltage used to accelerate the electrons; the actual energy of each electron is this voltage times the electron charge. For context, the typical energy of a chemical bond is a few eV;[94] electron diffraction involves electrons up to 5,000,000 eV. The magnitude of the interaction of the electrons with a material scales as[1]: Chpt 4
While the wavevector increases as the energy increases, the change in the effective mass compensates this so even at the very high energies used in electron diffraction there are still significant interactions.[92] The high-energy electrons interact with the Coulomb potential,[33] which for a crystal can be considered in terms of a Fourier series (see for instance Ashcroft and Mermin),[6]: Chpt 8 that is
with a reciprocal lattice vector and the corresponding Fourier coefficient of the potential. The reciprocal lattice vector is often referred to in terms of Miller indices , a sum of the individual reciprocal lattice vectors with integers in the form:[3]
(Sometimes reciprocal lattice vectors are written as , , and see note.[lower-alpha 4]) The contribution from the needs to be combined with what is called the shape function (e.g.[95][96][1]: Chpt 2 ), which is the Fourier transform of the shape of the object. If, for instance, the object is small in one dimension then the shape function extends far in that direction in the Fourier transform—a reciprocal relationship.[97]
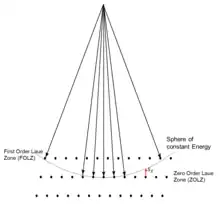
Around each reciprocal lattice point one has this shape function.[1]: Chpt 5-7 [7]: Chpt 2 How much intensity there will be in the diffraction pattern depends upon the intersection of the Ewald sphere, that is energy conservation, and the shape function around each reciprocal lattice point—see Figure 6, 20 and 22. The vector from a reciprocal lattice point to the Ewald sphere is called the excitation error .
For transmission electron diffraction the samples used are thin, so most of the shape function is along the direction of the electron beam. For both LEED[86] and RHEED[87] the shape function is mainly normal to the surface of the sample. In LEED this results in (a simplification) back-reflection of the electrons leading to spots, see Figure 20 and 21 later, whereas in RHEED the electrons reflect off the surface at a small angle and typically yield diffraction patterns with streaks, see Figure 22 and 23 later. By comparison, with both x-ray and neutron diffraction the scattering is significantly weaker,[1]: Chpt 4 so typically requires much larger crystals, in which case the shape function shrinks to just around the reciprocal lattice points, leading to simpler Bragg's law diffraction.[98]
For all cases, when the reciprocal lattice points are close to the Ewald sphere (the excitation error is small) the intensity tends to be higher; when they are far away it tends to be smaller. The set of diffraction spots at right angles to the direction of the incident beam are called the zero-order Laue zone (ZOLZ) spots, as shown in Figure 6. One can also have intensities further out from reciprocal lattice points which are in a higher layer. The first of these is called the first order Laue zone (FOLZ); the series is called by the generic name higher order Laue zone (HOLZ).[2]: Chpt 7 [99]
The result is that the electron wave after it has been diffracted can be written as an integral over different plane waves:[8]: Chpt 1
that is a sum of plane waves going in different directions, each with a complex amplitude . (This is a three dimensional integral, which is often written as rather than .) For a crystalline sample these wavevectors have to be of the same magnitude for elastic scattering (no change in energy), and are related to the incident direction by (see Figure 6)
A diffraction pattern detects the intensities
For a crystal these will be near the reciprocal lattice points typically forming a two dimensional grid. Different samples and modes of diffraction give different results, as do different approximations for the amplitudes .[1][2][4]
A typical electron diffraction pattern in TEM and LEED is a grid of high intensity spots (white) on a dark background, approximating a projection of the reciprocal lattice vectors, see Figure 1, 9, 10, 11, 14 and 21 later. There are also cases which will be mentioned later where diffraction patterns are not periodic, see Figure 15, have additional diffuse structure as in Figure 16, or have rings as in Figure 12, 13 and 24. With conical illumination as in CBED they can also be a grid of discs, see Figure 7, 9 and 18. RHEED is slightly different,[87] see Figure 22, 23. If the excitation errors were zero for every reciprocal lattice vector, this grid would be at exactly the spacings of the reciprocal lattice vectors. This would be equivalent to a Bragg's law condition for all of them. In TEM the wavelength is small and this is close to correct, but not exact. In practice the deviation of the positions from a simple Bragg's law[98] interpretation is often neglected, particularly if a column approximation is made (see below).[8]: 64 [7]: Chpt 11 [100]
Kinematical diffraction
In Kinematical theory an approximation is made that the electrons are only scattered once.[1]: Sec 2 For transmission electron diffraction it is common to assume a constant thickness , and also what is called the Column Approximation (e.g. references[7]: Chpt 11 [100] and further reading). For a perfect crystal the intensity for each diffraction spot is then:
where is the magnitude of the excitation error along z, the distance along the beam direction (z-axis by convention) from the diffraction spot to the Ewald sphere, and is the structure factor:[3]
the sum being over all the atoms in the unit cell with the form factors,[3] the reciprocal lattice vector, is a simplified form of the Debye–Waller factor,[3] and is the wavevector for the diffraction beam which is:
for an incident wavevector of , as in Figure 6 and above. The excitation error comes in as the outgoing wavevector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): \mathbf {k} has to have the same modulus (i.e. energy) as the incoming wavevector . The intensity in transmission electron diffraction oscillates as a function of thickness, which can be confusing; there can similarly be intensity changes due to variations in orientation and also structural defects such as dislocations.[101] If a diffraction spot is strong it could be because it has a larger structure factor, or it could be because the combination of thickness and excitation error is "right". Similarly the observed intensity can be small, even though the structure factor is large. This can complicate interpretation of the intensities. By comparison, these effects are much smaller in x-ray diffraction or neutron diffraction because they interact with matter far less and often Bragg's law[98] is adequate.
This form is a reasonable first approximation which is qualitatively correct in many cases, but more accurate forms including multiple scattering (dynamical diffraction) of the electrons are needed to properly understand the intensities.[1]: Sec 3 [8]: Chpt 3-5
Dynamical diffraction
While kinematical diffraction is adequate to understand the geometry of the diffraction spots, it does not correctly give the intensities and has a number of other limitations. For a more complete approach one has to include multiple scattering of the electrons using methods that date back to the early work of Hans Bethe in 1928.[33] These are based around solutions of the Schrödinger equation[11] using the relativistic effective mass described earlier.[92] Even at very high energies dynamical diffraction is needed as the relativistic mass and wavelength partially cancel, so the role of the potential is larger than might be thought.[92][93]

The main components of current dynamical diffraction of electrons include:
- Taking into account the scattering back into the incident beam both from diffracted beams and between all others, not just single scattering from the incident beam to diffracted beams.[33] This is important even for samples which are only a few atoms thick.[33][62]
- Modelling at least semi-empirically the role of inelastic scattering by an imaginary component of the potential,[102][103][104] also called an "optical potential".[8]: Chpt 13 There is always inelastic scattering, and often it can have a major effect on both the background and sometimes the details, see Figure 7 and 18.[102][103][104]
- Higher-order numerical approaches to calculate the intensities such as multislice,[65][105] matrix methods[106][8]: Sec 4.3 which are called Bloch-wave approaches or muffin-tin approaches.[107] With these diffraction spots which are not present in kinematical theory can be present, e.g.[108]
- Contributions to the diffraction from elastic strain and crystallographic defects, and also what Jens Lindhard called the string potential.[109]
- For transmission electron microscopes effects due to variations in the thickness of the sample and the normal to the surface.[1]: Chpt 6
- Both in the geometry of scattering and calculations, for both LEED[110] and RHEED,[111][10] effects due to the presence of surface steps, surface reconstructions and other atoms at the surface. Often these change the diffraction details significantly.[110][111][10]
- For LEED, use more careful analyses of the potential because contributions from exchange terms can be important.[9] Without these the calculations may not be accurate enough.[9]
Kikuchi lines
Kikuchi lines,[112][2]: 311–313 first observed by Seishi Kikuchi in 1928,[34][35] are linear features created by electrons scattered both inelastically and elastically. As the electron beam interacts with matter, the electrons are diffracted via elastic scattering, and also scattered inelastically losing part of their energy. These occur simultaneously, and cannot be separated – according to the Copenhagen interpretation of quantum mechanics, only the probabilities of electrons at detectors can be measured.[113][114] These electrons form Kikuchi lines which provide information on the orientation.[115]

Kikuchi lines come in pairs forming Kikuchi bands, and are indexed in terms of the crystallographic planes they are connected to, with the angular width of the band equal to the magnitude of the corresponding diffraction vector . The position of Kikuchi bands is fixed with respect to each other and the orientation of the sample, but not against the diffraction spots or the direction of the incident electron beam. As the crystal is tilted, the bands move on the diffraction pattern.[115] Since the position of Kikuchi bands is quite sensitive to crystal orientation, they can be used to fine-tune a zone-axis orientation or determine crystal orientation. They can also be used for navigation when changing the orientation between zone axes connected by some band, an example of such a map produced by combining many local sets of experimental Kikuchi patterns is in Figure 8; Kikuchi maps are available for many materials.
Types and techniques
In a transmission electron microscope
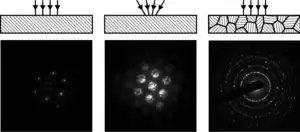
Electron diffraction in a TEM exploits controlled electron beams using electron optics.[116] Different types of diffraction experiments, for instance Figure 9, provide information such as lattice constants, symmetries, and sometimes to solve an unknown crystal structure.
It is common to combine it with other methods, for instance images using selected diffraction beams, high-resolution images[117] showing the atomic structure, chemical analysis through energy-dispersive x-ray spectroscopy,[118] investigations of electronic structure and bonding through electron energy loss spectroscopy,[119] and studies of the electrostatic potential through electron holography;[120] this list is not exhaustive. Compared to x-ray crystallography, TEM analysis is significantly more localized and can be used to obtain information from tens of thousands of atoms to just a few or even single atoms.
Formation of a diffraction pattern
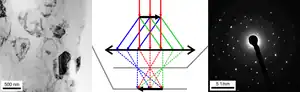
In TEM, the electron beam passes through a thin film of the material as illustrated in Figure 10. Before and after the sample the beam is manipulated by the electron optics[116] including magnetic lenses, deflectors and apertures;[121] these act on the electrons similar to how glass lenses focus and control light. Optical elements above the sample are used to control the incident beam which can range from a wide and parallel beam to one which is a converging cone and can be smaller than an atom, 0.1 nm. As it interacts with the sample, part of the beam is diffracted and part is transmitted without changing its direction. This occurs simultaneously as electrons are everywhere until they are detected (wavefunction collapse) according to the Copenhagen interpretation.[113][114]
Below the sample, the beam is controlled by another set of magnetic lneses and apertures.[116] Each set of initially parallel rays (a plane wave) is focused by the first lens (objective) to a point in the back focal plane of this lens, forming a spot on a detector; a map of these directions, often an array of spots, is the diffraction pattern. Alternatively the lenses can form a magnified image of the sample.[116] Herein the focus is on collecting a diffraction pattern; for other information see the pages on TEM and scanning transmission electron microscopy.
Selected area electron diffraction
The simplest diffraction technique in TEM is selected area electron diffraction (SAED) where the incident beam is wide and close to parallel.[7]: Chpt 5-6 An aperture is used to select a particular region of interest from which the diffraction is collected. These apertures are part of a thin foil of a heavy metal such as tungsten[121] which has a number of small holes in it. This way diffraction information can be limited to, for instance, individual crystallites. Unfortunately the method is limited by the spherical aberration of the objective lens,[7]: Chpt 5-6 so is only accurate for large grains with tens of thousands of atoms or more; for smaller regions a focused probe is needed.[7]: Chpt 5-6
If a parallel beam is used to acquire a diffraction pattern from a single-crystal, the result is similar to a two-dimensional projection of the crystal reciprocal lattice. From this one can determine interplanar distances and angles and in some cases crystal symmetry, particularly when the electron beam is down a major zone axis, see for instance the database by Jean-Paul Morniroli.[78] However, projector lens aberrations such as barrel distortion as well as dynamical diffraction effects (e.g.[122]) cannot be ignored. For instance, certain diffraction spots which are not present in x-ray diffraction can appear,[78] for instance those due to Gjønnes-Moodie extinction conditions.[108]

If the sample is tilted relative to the electron beam, different sets of crystallographic planes contribute to the pattern yielding different types of diffraction patterns, approximately different projections of the reciprocal lattice, see Figure 11.[78] This can be used to determine the crystal orientation, which in turn can be used to set the orientation needed for a particular experiment. Furthermore, a series of diffraction patterns varying in tilt can be acquired and processed using a diffraction tomography approach. There are ways to combine this with direct methods algorithms using electrons[123][80] and other methods such as charge flipping,[81] or automated diffraction tomography[124][125] to solve crystal structures.
Polycrystalline pattern
Diffraction patterns depend on whether the beam is diffracted by one single crystal or by a number of differently oriented crystallites, for instance in a polycrystalline material. If there are many contributing crystallites, the diffraction image is a superposition of individual crystal patterns, see Figure 12. With a large number of grains this superposition yields diffraction spots of all possible reciprocal lattice vectors. This results in a pattern of concentric rings as shown in Figure 12 and 13.[7]: Chpt 5-6


Textured materials yield a non-uniform distribution of intensity around the ring, which can be used to discriminate between nanocrystalline and amorphous phases. However, diffraction often cannot differentiate between very small grain polycrystalline materials and truly random order amorphous.[126] Here high-resolution transmission electron microscopy[127] and fluctuation electron microscopy[128][129] can be more powerful, although this is still a topic of continuing development.
Multiple materials and double diffraction
In simple cases there is only one grain or one type of material in the area used for collecting a diffraction pattern. However, often there is more than one. If they are in different areas then the diffraction pattern will be a combination.[7]: Chpt 5-6 In addition there can be one grain on top of another, in which case the electrons that go through the first are diffracted by the second.[7]: Chpt 5-6 Electrons have no memory (like many of us), so after they have gone through the first grain and been diffracted, they traverse the second as if their current direction was that of the incident beam. This leads to diffraction spots which are the vector sum of those of the two (or even more) reciprocal lattices of the crystals, and can lead to complicated results. It can be difficult to know if this is real and due to some novel material, or just a case where multiple crystals and diffraction is leading to odd results.[7]: Chpt 5-6
Bulk and surface superstructures
Many materials have relatively simple structures based upon small unit cell vectors (see also note[lower-alpha 4]). There are many others where the repeat is some larger multiple of the smaller unit cell (subcell) along one or more direction, for instance . which has larger dimensions in two directions. These superstructures[130][131][132] can arise from many reasons:
- Larger unit cells due to electronic ordering which leads to small displacements of the atoms in the subcell. One example is antiferroelectricity ordering.[133]
- Chemical ordering, that is different atom types at different locations of the subcell.[134]
- Magnetic order of the spins. These may be in opposite directions on some atoms, leading to what is called antiferromagnetism.[135]
_7x7.png.webp)
In addition to those which occur in the bulk, superstructures can also occur at surfaces. When half the material is (nominally) removed to create a surface, some of the atoms will be under coordinated. To reduce their energy they can rearrange. Sometimes these rearrangements are relatively small; sometimes they are quite large.[136][137] Similar to a bulk superstructure there will be additional, weaker diffraction spots. One example is for the silicon (111) surface, where there is a supercell which is seven times larger than the simple bulk cell in two directions.[138] This leads to diffraction patterns with additional spots some of which are marked in Figure 14.[139] Here the (220) are stronger bulk diffraction spots, and the weaker ones due to the surface reconstruction are marked 7x7—see note[lower-alpha 4] for convention comments.
Aperiodic materials

In an aperiodic crystal the structure can no longer be simply described by three different vectors in real or reciprocal space. In general there is a substructure describable by three (e.g. ), similar to supercells above, but in addition there is some additional periodicity (one to three) which cannot be described as a multiple of the three; it is a genuine additional periodicity which is an irrational number relative to the subcell lattice.[130][131][132] The diffraction pattern can then only be described by more than three indices.
An extreme example of this is for quasicrystals,[140] which can be described similarly by a higher number of Miller indices in reciprocal space—but not by any translational symmetry in real space. An example of this is shown in Figure 15 for an Al-Cu-Fe-Cr decagonal quasicrystal grown by magnetron sputtering on a sodium chloride substrate and then lifted off by dissolving the substrate with water.[141] In the pattern there are pentagons which are a characteristic of the aperiodic nature of these materials.
Diffuse scattering

A further step beyond superstructures and aperiodic materials is what is called diffuse scattering in electron diffraction patterns due to disorder,[1]: Chpt 17 which is also known for x-ray[142] or neutron[143] scattering. This can occur from inelastic processes, for instance, in bulk silicon the atomic vibrations (phonons) are more prevalent along specific directions, which leads to streaks in diffraction patterns.[1]: Chpt 12 Sometimes it is due to arrangements of point defects. Completely disordered substitutional point defects lead to a general background which is called Laue monotonic scattering.[1]: Chpt 12 Often there is a probability distribution for the distances between point defects or what type of substitutional atom there is, which leads to distinct three-dimensional intensity features in diffraction patterns. An example of this is for a Nb0.83CoSb sample, with the diffraction pattern shown in Figure 16. Because of the vacancies at the niobium sites, there is diffuse intensity with snake-like structure due to correlations of the distances between vacancies and also the relaxation of Co and Sb atoms around these vacancies.[144]
Convergent beam electron diffraction

In convergent beam electron diffraction (CBED),[71][73][75] the incident electrons are normally focused in a converging cone-shaped beam with a crossover located at the sample, e.g. Figure 17, although other methods exist. Unlike the parallel beam, the convergent beam is able to carry information from the sample volume, not just a two-dimensional projection available in SAED. With convergent beam there is also no need for the selected area aperture, as it is inherently site-selective since the beam crossover is positioned at the object plane where the sample is located.[115]
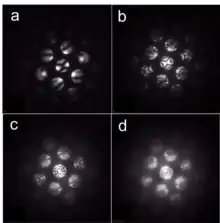
A CBED pattern consists of disks arranged similar to the spots in SAED. Intensity within the disks represents dynamical diffraction effects and symmetries of the sample structure, see Figure 7 and 18. Even though the zone axis and lattice parameter analysis based on disk positions does not significantly differ from SAED, the analysis of disks content is more complex and simulations based on dynamical diffraction theory is often required.[145] As illustrated in Figure 18, the details within the disk change with sample thickness, as does the inelastic background. With appropriate analysis CBED patterns can be used for indexation of the crystal point group, space group identification, measurement of lattice parameters, thickness or strain.[115]
The disk diameter can be controlled using the microscope optics and apertures.[116] The larger is the angle, the broader the disks are with more features. If the angle is increased to significantly, the disks begin to overlap.[70] This is avoided in large angle convergent electron beam diffraction (LACBED) where the sample is moved upwards or downwards. There are applications, however, where the overlapping disks are beneficial, for instance with a ronchigram. It is a CBED pattern, often but not always of an amorphous material, with many intentionally overlapping disks providing information about the optical aberrations of the electron optical system.[146]
Precession electron diffraction
.gif)
Precession electron diffraction (PED), invented by Roger Vincent and Paul Midgley in 1994,[148] is a method to collect electron diffraction patterns in a transmission electron microscope (TEM). The technique involves rotating (precessing) a tilted incident electron beam around the central axis of the microscope, compensating for the tilt after the sample so a spot diffraction pattern is formed, similar to a SAED pattern. However, a PED pattern is an integration over a collection of diffraction conditions, see Figure 19. This integration produces a quasi-kinematical diffraction pattern that is more suitable[149] as input into direct methods algorithms using electrons[123][80] to determine the crystal structure of the sample. Because it avoids many dynamical effects it can also be used to better identify crystallographic phases.[150]
4D STEM
4D scanning transmission electron microscopy (4D STEM)[151] is a subset of scanning transmission electron microscopy (STEM) methods which uses a pixelated electron detector to capture a convergent beam electron diffraction (CBED) pattern at each scan location; see the main page for further information. This technique captures a 2 dimensional reciprocal space image associated with each scan point as the beam rasters across a 2 dimensional region in real space, hence the name 4D STEM. Its development was enabled by better STEM detectors and improvements in computational power. The technique has applications in diffraction contrast imaging, phase orientation and identification, strain mapping, and atomic resolution imaging among others; it has become very popular and rapidly evolving from about 2020 onwards.[151]
The name 4D STEM is common in literature, however it is known by other names: 4D STEM EELS, ND STEM (N- since the number of dimensions could be higher than 4), position resolved diffraction (PRD), spatial resolved diffractometry, momentum-resolved STEM, "nanobeam precision electron diffraction", scanning electron nano diffraction, nanobeam electron diffraction, or pixelated STEM.[152] Most of these are the same, although there are instances such as momentum-resolved STEM[153] where the emphasis can be very different.
Low-energy electron diffraction (LEED)
Low-energy electron diffraction (LEED) is a technique for the determination of the surface structure of single-crystalline materials by bombardment with a collimated beam of low-energy electrons (30–200 eV).[83] In this case the Ewald sphere leads to approximately back-reflection, as illustrated in Figure 20, and diffracted electrons as spots on a fluorescent screen as shown in Figure 21; see the main page for more information and references.[58][86] It has been used to solve a very large number of relatively simple surface structures of metals and semiconductors, plus cases with simple chemisorbants. For more complex cases transmission electron diffraction[138][154] or surface x-ray diffraction[155] have been used, often combined with scanning tunneling microscopy and density functional theory calculations.[156]
LEED may be used in one of two ways:[58][86]
- Qualitatively, where the diffraction pattern is recorded and analysis of the spot positions gives information on the symmetry of the surface structure. In the presence of an adsorbate the qualitative analysis may reveal information about the size and rotational alignment of the adsorbate unit cell with respect to the substrate unit cell.[58]
- Quantitatively, where the intensities of diffracted beams are recorded as a function of incident electron beam energy to generate the so-called I–V curves. By comparison with theoretical curves, these may provide accurate information on atomic positions on the surface.[86]
Reflection high-energy electron diffraction (RHEED)
Reflection high energy electron diffraction (RHEED),[87] is a technique used to characterize the surface of crystalline materials by reflecting electrons off a surface. As illustrated for the Ewald sphere construction in Figure 22, it uses mainly the higher-order Laue zones which have a reflection component. An experimental diffraction pattern is shown in Figure 23 and shows both rings from the higher-order Laue zones and streaky spots.[8]: Chpt 5 RHEED systems gather information only from the surface layers of the sample, which distinguishes RHEED from other materials characterization methods that also rely on diffraction of electrons. Transmission electron microscopy samples mainly the bulk of the sample, although in special cases it can provide surface information.[157] Low-energy electron diffraction (LEED) is also surface sensitive, and achieves surface sensitivity through the use of low energy electrons. The main uses of RHEED to date have been during thin film growth,[158] as the geometry is amenable to simultaneous collection of the diffraction data and deposition. It can, for instance, be used to monitor surface roughness during growth by looking at both the shapes of the streaks in the diffraction pattern as well as variations in the intensities.[87][158]
Gas electron diffraction

Gas electron diffraction (GED) can be used to determine the geometry of molecules in gases.[159] A gas carrying the molecules is exposed to the electron beam, which is diffracted by the molecules. Since the molecules are randomly oriented, the resulting diffraction pattern consists of broad concentric rings, see Figure 24. The diffraction intensity is a sum of several components such as background, atomic intensity or molecular intensity.[159]
In GED the diffraction intensities at a particular diffraction angle is described via a scattering variable defined as[160]
The total intensity is then given as a sum of partial contributions:[161][162]
where results from scattering by individual atoms, by pairs of atoms and by atom triplets. Intensity corresponds to the background which, unlike the previous contributions, must be determined experimentally. The intensity of atomic scattering is defined as[159]
where , is the distance between the scattering object detector, is the intensity of the primary electron beam and is the scattering amplitude of the atom of the molecular structure in the experiment. is the main contribution and easily obtained for known gas composition. Note that the vector used here is not the same as the excitation error used in other areas of diffraction, see earlier. The most valuable information is carried by the intensity of molecular scattering , as it contains information about the distance between all pairs of atoms in the molecule. It is given by[160]
where is the distance between two atoms, is the mean square amplitude of vibration between the two atoms, similar to a Debye–Waller factor, is the anharmonicity constant and a phase factor which is important for atomic pairs with very different nuclear charges. The summation is performed over all atom pairs. Atomic triplet intensity is negligible in most cases. If the molecular intensity is extracted from an experimental pattern by subtracting other contributions, it can be used to match and refine a structural model against the experimental data.[160][161][162]
Similar methods of analysis have also been applied to analyze electron diffraction data from liquids.[163][164][165]
In a scanning electron microscope

In a scanning electron microscope the region near the surface can be mapped using an electron beam that is scanned in a grid across the sample. A diffraction pattern can be recorded using electron backscatter diffraction (EBSD), as illustrated in Figure 25, captured with a camera inside the microscope.[166] A depth from a few nanometers to a few microns, depending upon the electron energy used, is penetrated by the electrons, some of which are diffracted backwards and out of the sample. As result of combined inelastic and elastic scattering, typical features in an EBSD image are Kikuchi lines. Since the position of Kikuchi bands is highly sensitive to the crystal orientation, EBSD data can be used to determine the crystal orientation at particular locations of the sample. The data are processed by software yielding two-dimensional orientation maps.[167][168] As the Kikuchi lines carry information about the interplanar angles and distances and, therefore, about the crystal structure, they can also be used for phase identification[169]: Chpts 6-7 or strain analysis.[169]: Chpt 17
Notes
- 1 2 Sometimes electron diffraction is defined similar to light or water wave diffraction, that is interference or bending of (electron) waves around the corners of an obstacle or through an aperture. With this definition the electrons are behaving as waves in a general sense, corresponding to a type of Fresnel diffraction. However, in every case where electron diffraction is used in practice the obstacles of relevance are atoms, so the general definition is not used herein.
- ↑ In their first, shorter paper in Nature Davisson and Germer stated that their results were consistent with the de Broglie wavelength. Similarly Thomson and Reid used the de Broglie wavelength to explain their results. However, in their subsequently, more detailed papers Davisson and Germer specifically stated that their work was consistent with undulatory mechanics, and not consistent with the de Broglie wavelength. More importantly, the (non-relativistic) wavelength comes automatically from the Schrödinger equation, as do the equations for the amplitudes of electron diffraction; these cannot be derived from the de Broglie wavelength. As cited in the main text, Davisson and Germer were able to demonstrate that the diffraction angles were different from those of Bragg's Law, needing a proper treatment which includes the average potential inside the material. Since all theoretical models start from the Schrödinger equation (with relativistic terms included) this is really the key to electron diffraction, not the de Broglie wavelength. See matter waves for more discussion.
- ↑ Herein crystallographic conventions are used. Often in physics a plane wave is defined as . This changes some of the equations by a factor of , for instance appears instead of , but nothing significant.
- 1 2 3 4 Notations differ depending upon whether the source is crystallography, physics or other. In addition to for the reciprocal lattice vectors as used herein, sometimes are used. Less common, but still sometimes used, are for real space, and for reciprocal space. Also, sometimes reciprocal lattice vectors are written with capitals as not , and the length can differ by a factor of as mentioned above if is used for plane waves. (Different notations also exist for the wavevectors , or .) Similar notation differences can occur with aperiodic materials and superstructures. Furthermore, when dealing with surfaces as in LEED, normally two-dimensional real and reciprocal lattice vectors in the surface are used, defined in terms of a matrix multiplier of the simple surface unit cell when there are reconstructions. To make things slightly more complicated, frequently four Miller indices are used for hexagonal systems even though only three are needed.
References
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 John M., Cowley (1995). Diffraction physics. Elsevier. ISBN 0-444-82218-6. OCLC 247191522.
- 1 2 3 4 5 6 Reimer, Ludwig (2013). Transmission Electron Microscopy : Physics of Image Formation and Microanalysis. Springer Berlin / Heidelberg. ISBN 978-3-662-13553-2. OCLC 1066178493.
- 1 2 3 4 5 6 Colliex, C.; Cowley, J. M.; Dudarev, S. L.; Fink, M.; Gjønnes, J.; Hilderbrandt, R.; Howie, A.; Lynch, D. F.; Peng, L. M. (2006), Prince, E. (ed.), "Electron diffraction", International Tables for Crystallography (1 ed.), Chester, England: International Union of Crystallography, vol. C, pp. 259–429, doi:10.1107/97809553602060000593, ISBN 978-1-4020-1900-5
- 1 2 Humphreys, C J (1979). "The scattering of fast electrons by crystals". Reports on Progress in Physics. 42 (11): 1825–1887. doi:10.1088/0034-4885/42/11/002. ISSN 0034-4885. S2CID 250876999.
- 1 2 3 4 5 6 7 8 de Broglie, Louis Victor. "On the Theory of Quanta" (PDF). Foundation of Louis de Broglie (English translation by A.F. Kracklauer, 2004. ed.). Retrieved 25 February 2023.
- 1 2 3 Ashcroft, Neil W.; Mermin, N. David (2012). Solid state physics (Repr ed.). South Melbourne: Brooks/Cole Thomson Learning. ISBN 978-0-03-083993-1.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 Hirsch, P. B.; Howie, A.; Nicholson, R. B.; Pashley, D. W.; Whelan, M. J. (1965). Electron microscopy of thin crystals. London: Butterworths. ISBN 0-408-18550-3. OCLC 2365578.
- 1 2 3 4 5 6 7 Peng, L.-M.; Dudarev, S. L.; Whelan, M. J. (2011). High energy electron diffraction and microscopy. Oxford: Oxford University Press. ISBN 978-0-19-960224-7. OCLC 656767858.
- 1 2 3 4 Pendry, J B (1971). "Ion core scattering and low energy electron diffraction. I". Journal of Physics C: Solid State Physics. 4 (16): 2501–2513. Bibcode:1971JPhC....4.2501P. doi:10.1088/0022-3719/4/16/015. ISSN 0022-3719.
- 1 2 3 Maksym, P.A.; Beeby, J.L. (1981). "A theory of RHEED". Surface Science. 110 (2): 423–438. Bibcode:1981SurSc.110..423M. doi:10.1016/0039-6028(81)90649-X.
- 1 2 3 4 5 6 7 Schrödinger, E. (1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules". Physical Review. 28 (6): 1049–1070. Bibcode:1926PhRv...28.1049S. doi:10.1103/PhysRev.28.1049. ISSN 0031-899X.
- 1 2 3 4 Born, M.; Wolf, E. (1999). Principles of Optics. Cambridge University Press. ISBN 978-0-521-64222-4.
- ↑ Shipley, J.T. (1945). Dictionary of Word Origins. The Philosophical Library. p. 133. ISBN 978-0-88029-751-6.
- 1 2 Iversen, Paul; Lacks, Daniel J. (2012). "A life of its own: The tenuous connection between Thales of Miletus and the study of electrostatic charging". Journal of Electrostatics. 70 (3): 309–311. doi:10.1016/j.elstat.2012.03.002. ISSN 0304-3886.
- ↑ Harsch, Viktor (2007). "Otto von Gericke (1602–1686) and his pioneering vacuum experiments". Aviation, Space, and Environmental Medicine. 78 (11): 1075–1077. doi:10.3357/asem.2159.2007. ISSN 0095-6562. PMID 18018443.
- ↑ Michael Faraday (1838) "VIII. Experimental researches in electricity. — Thirteenth series.," Philosophical Transactions of the Royal Society of London, 128 : 125–168.
- ↑ Plücker, M. (1858). "XLVI. Observations on the electrical discharge through rarefied gases". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 16 (109): 408–418. doi:10.1080/14786445808642591. ISSN 1941-5982.
- 1 2 3 Martin, Andre (1986), "Cathode Ray Tubes for Industrial and Military Applications", in Hawkes, Peter (ed.), Advances in Electronics and Electron Physics, Volume 67, Academic Press, pp. 183–186, ISBN 9780080577333
- ↑ Goldstein, Eugen (1876). Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin (in German). The Academy. pp. 279–295, pp 286.
- ↑ Whittaker, E.T. (1951). A History of the Theories of Aether and Electricity. Vol. 1. London: Nelson.
- 1 2 Crookes, William (1878). "I. On the illumination of lines of molecular pressure, and the trajectory of molecules". Proceedings of the Royal Society of London. 28 (190–195): 103–111. doi:10.1098/rspl.1878.0098. ISSN 0370-1662. S2CID 122006529.
- ↑ Thomson, J. J. (1897). "XL. Cathode Rays". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 44 (269): 293–316. doi:10.1080/14786449708621070. ISSN 1941-5982.
- ↑ Stoney, George Johnstone (1891). "Cause of Double Lines in Spectra". The Scientific Transactions of the Royal Dublin Society. Dublin. 4: 563, pp 583.
- ↑ Einstein, Albert. Relativity: The Special and General Theory.
- ↑ Bohr, N. (1913). "On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 1–25. doi:10.1080/14786441308634955. ISSN 1941-5982.
- ↑ Davisson, C.; Germer, L. H. (1927). "The Scattering of Electrons by a Single Crystal of Nickel". Nature. 119 (2998): 558–560. Bibcode:1927Natur.119..558D. doi:10.1038/119558a0. ISSN 0028-0836. S2CID 4104602.
- 1 2 Davisson, C.; Germer, L. H. (1927). "Diffraction of Electrons by a Crystal of Nickel". Physical Review. 30 (6): 705–740. Bibcode:1927PhRv...30..705D. doi:10.1103/physrev.30.705. ISSN 0031-899X.
- 1 2 3 Davisson, C. J.; Germer, L. H. (1928). "Reflection of Electrons by a Crystal of Nickel". Proceedings of the National Academy of Sciences. 14 (4): 317–322. Bibcode:1928PNAS...14..317D. doi:10.1073/pnas.14.4.317. ISSN 0027-8424. PMC 1085484. PMID 16587341.
- 1 2 Davisson, C. J.; Germer, L. H. (1928). "Reflection and Refraction of Electrons by a Crystal of Nickel". Proceedings of the National Academy of Sciences. 14 (8): 619–627. Bibcode:1928PNAS...14..619D. doi:10.1073/pnas.14.8.619. ISSN 0027-8424. PMC 1085652. PMID 16587378.
- ↑ Thomson, G. P.; Reid, A. (1927). "Diffraction of Cathode Rays by a Thin Film". Nature. 119 (3007): 890. Bibcode:1927Natur.119Q.890T. doi:10.1038/119890a0. ISSN 0028-0836. S2CID 4122313.
- ↑ Reid, Alexander (1928). "The diffraction of cathode rays by thin celluloid films". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 119 (783): 663–667. Bibcode:1928RSPSA.119..663R. doi:10.1098/rspa.1928.0121. ISSN 0950-1207. S2CID 98311959.
- ↑ Navarro, Jaume (2010). "Electron diffraction chez Thomson: early responses to quantum physics in Britain". The British Journal for the History of Science. 43 (2): 245–275. doi:10.1017/S0007087410000026. ISSN 0007-0874. S2CID 171025814.
- 1 2 3 4 5 6 Bethe, H. (1928). "Theorie der Beugung von Elektronen an Kristallen". Annalen der Physik (in German). 392 (17): 55–129. Bibcode:1928AnP...392...55B. doi:10.1002/andp.19283921704.
- 1 2 Kikuchi, Seishi (1928). "Diffraction of cathode rays by mica". Proceedings of the Imperial Academy. 4 (6): 271–274. doi:10.2183/pjab1912.4.271. S2CID 4121059 – via Google Scholar.
- 1 2 Kikuchi, Seishi (1928). "Electron diffraction in single crystals". Japanese Journal of Physics. 5 (3061): 83–96.
- ↑ Mark, Herman; Wierl, Raymond (1930). "Neuere Ergebnisse der Elektronenbeugung". Die Naturwissenschaften. 18 (36): 778–786. Bibcode:1930NW.....18..778M. doi:10.1007/bf01497860. ISSN 0028-1042. S2CID 9815364.
- ↑ Mark, Herman; Wiel, Raymond (1930). "Die ermittlung von molekülstrukturen durch beugung von elektronen an einem dampfstrahl". Zeitschrift für Elektrochemie und angewandte physikalische Chemie. 36 (9): 675–676. doi:10.1002/bbpc.19300360921. S2CID 178706417.
- ↑ Maxwell, Louis R. (1933). "Electron Diffraction by Liquids". Physical Review. 44 (2): 73–76. Bibcode:1933PhRv...44...73M. doi:10.1103/PhysRev.44.73. ISSN 0031-899X.
- 1 2 Knoll, M.; Ruska, E. (1932). "Beitrag zur geometrischen Elektronenoptik. I". Annalen der Physik. 404 (5): 607–640. Bibcode:1932AnP...404..607K. doi:10.1002/andp.19324040506. ISSN 0003-3804.
- 1 2 Knoll, M.; Ruska, E. (1932). "Das Elektronenmikroskop". Zeitschrift für Physik (in German). 78 (5–6): 318–339. Bibcode:1932ZPhy...78..318K. doi:10.1007/BF01342199. ISSN 1434-6001. S2CID 186239132.
- ↑ Calbick, C. J. (1944). "Historical Background of Electron Optics". Journal of Applied Physics. 15 (10): 685–690. Bibcode:1944JAP....15..685C. doi:10.1063/1.1707371. ISSN 0021-8979.
- ↑ Hertz, Heinrich (2019), "Introduction to Heinrich Hertz's Miscellaneous Papers (1895) by Philipp Lenard", Heinrich Rudolf Hertz (1857–1894), Routledge, pp. 87–88, doi:10.4324/9780429198960-4, ISBN 978-0-429-19896-0, S2CID 195494352, retrieved 2023-02-24
- ↑ Wiechert, E. (1899). "Experimentelle Untersuchungen über die Geschwindigkeit und die magnetische Ablenkbarkeit der Kathodenstrahlen". Annalen der Physik und Chemie (in German). 305 (12): 739–766. Bibcode:1899AnP...305..739W. doi:10.1002/andp.18993051203.
- ↑ Wehnelt, A. (1905). "X. On the discharge of negative ions by glowing metallic oxides, and allied phenomena". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 10 (55): 80–90. doi:10.1080/14786440509463347. ISSN 1941-5982.
- ↑ Busch, H. (1926). "Berechnung der Bahn von Kathodenstrahlen im axialsymmetrischen elektromagnetischen Felde". Annalen der Physik (in German). 386 (25): 974–993. Bibcode:1926AnP...386..974B. doi:10.1002/andp.19263862507.
- 1 2 Mulvey, T (1962). "Origins and historical development of the electron microscope". British Journal of Applied Physics. 13 (5): 197–207. doi:10.1088/0508-3443/13/5/303. ISSN 0508-3443.
- ↑ Tao, Yaping (2018). "A Historical Investigation of the Debates on the Invention and Invention Rights of Electron Microscope". Proceedings of the 3rd International Conference on Contemporary Education, Social Sciences and Humanities (ICCESSH 2018). Advances in Social Science, Education and Humanities Research. Atlantis Press. pp. 1438–1441. doi:10.2991/iccessh-18.2018.313. ISBN 978-94-6252-528-3.
- ↑ Freundlich, Martin M. (1963). "Origin of the Electron Microscope: The history of a great invention, and of a misconception concerning the inventors, is reviewed". Science. 142 (3589): 185–188. doi:10.1126/science.142.3589.185. ISSN 0036-8075. PMID 14057363.
- ↑ Rüdenberg, Reinhold (2010), Origin and Background of the Invention of the Electron Microscope, Advances in Imaging and Electron Physics, vol. 160, Elsevier, pp. 171–205, doi:10.1016/s1076-5670(10)60005-5, ISBN 9780123810175, retrieved 2023-02-11.
- ↑ "Max Knoll". AncientFaces. Retrieved 2023-09-26.
- ↑ Rüdenberg, Reinhold. "Apparatus for producing images of objects". Patent Public Search Basic. Retrieved 24 February 2023.
- ↑ Rüdenberg, Reinhold. "Apparatus for producing images of objects". Patent Public Search Basic. Retrieved 24 February 2023.
- ↑ Rodenberg, R. (1932). "Elektronenmikroskop". Die Naturwissenschaften (in German). 20 (28): 522. Bibcode:1932NW.....20..522R. doi:10.1007/BF01505383. ISSN 0028-1042. S2CID 263996652.
- ↑ "Orbituary of Reinhold Rudenberg". pubs.aip.org. April 1962. doi:10.1063/1.3058109. Retrieved 2023-09-26.
- ↑ Boersch, H. (1936). "Über das primäre und sekundäre Bild im Elektronenmikroskop. II. Strukturuntersuchung mittels Elektronenbeugung". Annalen der Physik (in German). 419 (1): 75–80. Bibcode:1936AnP...419...75B. doi:10.1002/andp.19364190107.
- ↑ Germer, L. H. (1929). "Eine Anwendung der Elektronenbeugung auf die Untersuchung der Gasadsorption". Zeitschrift für Physik (in German). 54 (5–6): 408–421. Bibcode:1929ZPhy...54..408G. doi:10.1007/BF01375462. ISSN 1434-6001. S2CID 121097655.
- ↑ Farnsworth, H. E. (1932). "Diffraction of Low-Speed Electrons by Single Crystals of Copper and Silver". Physical Review. 40 (5): 684–712. Bibcode:1932PhRv...40..684F. doi:10.1103/PhysRev.40.684. ISSN 0031-899X.
- 1 2 3 4 Van Hove, Michel A.; Weinberg, William H.; Chan, Chi-Ming (1986). Low-Energy Electron Diffraction. Springer-Verlag, Berlin Heidelberg New York. pp. 13–426. ISBN 978-3-540-16262-9.
- ↑ Goodman, P. (Peter), ed. (1981). Fifty years of electron diffraction : in recognition of fifty years of achievement by the crystallographers and gas diffractionists in the field of electron diffraction. Dordrecht, Holland: Published for the International Union of Crystallography by D. Reidel. ISBN 90-277-1246-8. OCLC 7276396.
- ↑ Sewell, P. B.; Cohen, M. (1965). "The Observation Of Gas Adsorption Phenomena By Reflection High-Energy Electron Diffraction". Applied Physics Letters. 7 (2): 32–34. Bibcode:1965ApPhL...7...32S. doi:10.1063/1.1754284. ISSN 0003-6951.
- ↑ Laschkarew, W. E.; Usyskin, I. D. (1933). "Die Bestimmung der Lage der Wasserstoffionen im NH4Cl-Kristallgitter durch Elektronenbeugung". Zeitschrift für Physik (in German). 85 (9–10): 618–630. Bibcode:1933ZPhy...85..618L. doi:10.1007/BF01331003. ISSN 1434-6001. S2CID 123199621.
- 1 2 Cowley, J. M. (1953). "Structure analysis of single crystals by electron diffraction. II. Disordered boric acid structure". Acta Crystallographica. 6 (6): 522–529. Bibcode:1953AcCry...6..522C. doi:10.1107/S0365110X53001423. ISSN 0365-110X. S2CID 94391285.
- ↑ Zachariasen, W. H. (1954). "The precise structure of orthoboric acid". Acta Crystallographica. 7 (4): 305–310. Bibcode:1954AcCry...7..305Z. doi:10.1107/S0365110X54000886. ISSN 0365-110X.
- ↑ Cowley, J.M. (1968). "Crystal structure determination by electron diffraction". Progress in Materials Science. 13: 267–321. doi:10.1016/0079-6425(68)90023-6.
- 1 2 Cowley, J. M.; Moodie, A. F. (1957). "The scattering of electrons by atoms and crystals. I. A new theoretical approach". Acta Crystallographica. 10 (10): 609–619. Bibcode:1957AcCry..10..609C. doi:10.1107/S0365110X57002194. ISSN 0365-110X.
- ↑ Ishizuka, Kazuo (2004). "FFT Multislice Method—The Silver Anniversary". Microscopy and Microanalysis. 10 (1): 34–40. Bibcode:2004MiMic..10...34I. doi:10.1017/S1431927604040292. ISSN 1431-9276. PMID 15306065. S2CID 8016041.
- ↑ Goodman, P.; Moodie, A. F. (1974). "Numerical evaluations of N -beam wave functions in electron scattering by the multi-slice method". Acta Crystallographica Section A. 30 (2): 280–290. Bibcode:1974AcCrA..30..280G. doi:10.1107/S056773947400057X. ISSN 0567-7394.
- ↑ Cooley, James W.; Tukey, John W. (1965). "An algorithm for the machine calculation of complex Fourier series". Mathematics of Computation. 19 (90): 297–301. doi:10.1090/S0025-5718-1965-0178586-1. ISSN 0025-5718.
- ↑ Brigham, E. O.; Morrow, R. E. (1967). "The fast Fourier transform". IEEE Spectrum. 4 (12): 63–70. doi:10.1109/mspec.1967.5217220. S2CID 20294294. Retrieved 2023-09-26.
- 1 2 3 Kossel, W.; Möllenstedt, G. (1939). "Elektroneninterferenzen im konvergenten Bündel". Annalen der Physik (in German). 428 (2): 113–140. Bibcode:1939AnP...428..113K. doi:10.1002/andp.19394280204.
- 1 2 Goodman, P.; Lehmpfuhl, G. (1968). "Observation of the breakdown of Friedel's law in electron diffraction and symmetry determination from zero-layer interactions". Acta Crystallographica Section A. 24 (3): 339–347. Bibcode:1968AcCrA..24..339G. doi:10.1107/S0567739468000677.
- 1 2 Buxton, B. F.; Eades, J. A.; Steeds, John Wickham; Rackham, G. M.; Frank, Frederick Charles (1976). "The symmetry of electron diffraction zone axis patterns". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 281 (1301): 171–194. Bibcode:1976RSPTA.281..171B. doi:10.1098/rsta.1976.0024. S2CID 122890943.
- 1 2 Steeds, J. W.; Vincent, R. (1983). "Use of high-symmetry zone axes in electron diffraction in determining crystal point and space groups". Journal of Applied Crystallography. 16 (3): 317–324. Bibcode:1983JApCr..16..317S. doi:10.1107/S002188988301050X. ISSN 0021-8898.
- ↑ Bird, D. M. (1989). "Theory of zone axis electron diffraction". Journal of Electron Microscopy Technique. 13 (2): 77–97. doi:10.1002/jemt.1060130202. ISSN 0741-0581. PMID 2681572.
- 1 2 Tanaka, M.; Saito, R.; Sekii, H. (1983). "Point-group determination by convergent-beam electron diffraction". Acta Crystallographica Section A. 39 (3): 357–368. Bibcode:1983AcCrA..39..357T. doi:10.1107/S010876738300080X. ISSN 0108-7673.
- ↑ Tanaka, M.; Saito, R.; Watanabe, D. (1980). "Symmetry determination of the room-temperature form of LnNbO 4 (Ln = La,Nd) by convergent-beam electron diffraction". Acta Crystallographica Section A. 36 (3): 350–352. Bibcode:1980AcCrA..36..350T. doi:10.1107/S0567739480000800. ISSN 0567-7394. S2CID 98184340.
- ↑ Spence, J. C. H.; Zuo, J. M. (1992). Electron Microdiffraction. Boston, MA: Springer US. doi:10.1007/978-1-4899-2353-0. ISBN 978-1-4899-2355-4. S2CID 45473741.
- 1 2 3 4 Morniroli, Jean-Paul (2015). The atlas of electron diffraction zone axis patterns. Webpage and hardcopy.
{{cite book}}: CS1 maint: location missing publisher (link) - 1 2 Marks, Laurence (2012). Kolb, Ute; Shankland, Kenneth; Meshi, Louisa; Avilov, Anatoly; David, William I.F (eds.). Uniting Electron Crystallography and Powder Diffraction. NATO Science for Peace and Security Series B: Physics and Biophysics. Dordrecht: Springer Netherlands. pp. 281–291. Bibcode:2012uecp.book.....K. doi:10.1007/978-94-007-5580-2. ISBN 978-94-007-5579-6.
- 1 2 3 White, T.A.; Eggeman, A.S.; Midgley, P.A. (2010). "Is precession electron diffraction kinematical? Part I". Ultramicroscopy. 110 (7): 763–770. doi:10.1016/j.ultramic.2009.10.013. PMID 19910121.
- 1 2 Palatinus, Lukáš (2013). "The charge-flipping algorithm in crystallography". Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials. 69 (1): 1–16. Bibcode:2013AcCrB..69....1P. doi:10.1107/S2052519212051366. ISSN 2052-5192. PMID 23364455.
- 1 2 Alpert, D. (1953). "New Developments in the Production and Measurement of Ultra High Vacuum". Journal of Applied Physics. 24 (7): 860–876. Bibcode:1953JAP....24..860A. doi:10.1063/1.1721395. ISSN 0021-8979.
- 1 2 K. Oura; V. G. Lifshifts; A. A. Saranin; A. V. Zotov; M. Katayama (2003). Surface Science. Springer-Verlag, Berlin Heidelberg New York. pp. 1–45. ISBN 9783540005452.
- ↑ Kambe, Kyozaburo (1967). "Theory of Low-Energy Electron Diffraction". Zeitschrift für Naturforschung A. 22 (3): 322–330. doi:10.1515/zna-1967-0305. ISSN 1865-7109. S2CID 96851585.
- ↑ McRae, E.G. (1968). "Electron diffraction at crystal surfaces". Surface Science. 11 (3): 479–491. doi:10.1016/0039-6028(68)90058-7.
- 1 2 3 4 5 Moritz, Wolfgang; Van Hove, Michel (2022). Surface structure determination by LEED and X-rays. Cambridge, United Kingdom. pp. Chpt 3–5. ISBN 978-1-108-28457-8. OCLC 1293917727.
{{cite book}}: CS1 maint: location missing publisher (link) - 1 2 3 4 5 Ichimiya, Ayahiko; Cohen, Philip (2004). Reflection high-energy electron diffraction. Cambridge, U.K.: Cambridge University Press. pp. Chpt 4–19. ISBN 0-521-45373-9. OCLC 54529276.
- 1 2 3 Spence, J. C. H.; Zuo, J. M. (1988). "Large dynamic range, parallel detection system for electron diffraction and imaging". Review of Scientific Instruments. 59 (9): 2102–2105. Bibcode:1988RScI...59.2102S. doi:10.1063/1.1140039. ISSN 0034-6748.
- 1 2 3 Faruqi, A. R.; Cattermole, D. M.; Henderson, R.; Mikulec, B.; Raeburn, C. (2003). "Evaluation of a hybrid pixel detector for electron microscopy". Ultramicroscopy. 94 (3): 263–276. doi:10.1016/S0304-3991(02)00336-4. ISSN 0304-3991. PMID 12524196.
- 1 2 Schiff, Leonard I. (1987). Quantum mechanics. International series in pure and applied physics (3. ed., 24. print ed.). New York: McGraw-Hill. ISBN 978-0-07-085643-1.
- ↑ Watanabe, K.; Hara, S.; Hashimoto, I. (1996). "A Relativistic n -Beam Dynamical Theory for Fast Electron Diffraction". Acta Crystallographica Section A. 52 (3): 379–384. Bibcode:1996AcCrA..52..379W. doi:10.1107/S0108767395015893. ISSN 0108-7673.
- 1 2 3 4 5 Fujiwara, Kunio (1961). "Relativistic Dynamical Theory of Electron Diffraction". Journal of the Physical Society of Japan. 16 (11): 2226–2238. Bibcode:1961JPSJ...16.2226F. doi:10.1143/JPSJ.16.2226. ISSN 0031-9015.
- 1 2 Howie, A (1962). "Discussion of K. Fujiwara's paper by M. J. Whelan". Journal of the Physical Society of Japan. 17(Supplement BII): 118.
- ↑ "Bond Energies". Chemistry LibreTexts. 2013-10-02. Retrieved 2023-09-26.
- ↑ Vainstein, B.K. (1964), "Experimental Electron Diffraction Structure Investigations", Structure Analysis by Electron Diffraction, Elsevier, pp. 295–390, doi:10.1016/b978-0-08-010241-2.50010-9, ISBN 9780080102412, retrieved 2023-02-11
- ↑ Rees, A. L. G.; Spink, J. A. (1950). "The shape transform in electron diffraction by small crystals". Acta Crystallographica. 3 (4): 316–317. Bibcode:1950AcCry...3..316R. doi:10.1107/s0365110x50000823. ISSN 0365-110X.
- ↑ "Kevin Cowtan's Book of Fourier, University of York, UK". www.ysbl.york.ac.uk. Retrieved 2023-09-26.
- 1 2 3 Bragg, W.H.; Bragg, W.L. (1913). "The reflection of X-rays by crystals". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 88 (605): 428–438. Bibcode:1913RSPSA..88..428B. doi:10.1098/rspa.1913.0040. ISSN 0950-1207. S2CID 13112732.
- ↑ "higher-order Laue zone (HOLZ) reflection | Glossary | JEOL Ltd". higher-order Laue zone (HOLZ) reflection | Glossary | JEOL Ltd. Retrieved 2023-10-02.
- 1 2 Tanaka, Nobuo (2017), "Column Approximation and Howie-Whelan's Method for Dynamical Electron Diffraction", Electron Nano-Imaging, Tokyo: Springer Japan, pp. 293–296, doi:10.1007/978-4-431-56502-4_27, ISBN 978-4-431-56500-0, retrieved 2023-02-11
- ↑ Hirsch, Peter; Whelan, Michael (1960). "A kinematical theory of diffraction contrast of electron transmission microscope images of dislocations and other defects". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 252 (1017): 499–529. Bibcode:1960RSPTA.252..499H. doi:10.1098/rsta.1960.0013. ISSN 0080-4614. S2CID 123349515.
- 1 2 Yoshioka, Hide (1957). "Effect of Inelastic Waves on Electron Diffraction". Journal of the Physical Society of Japan. 12 (6): 618–628. Bibcode:1957JPSJ...12..618Y. doi:10.1143/JPSJ.12.618. ISSN 0031-9015.
- 1 2 Howie, Archibald; Whelan, Michael (1961). "Diffraction contrast of electron microscope images of crystal lattice defects – II. The development of a dynamical theory". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 263 (1313): 217–237. Bibcode:1961RSPSA.263..217H. doi:10.1098/rspa.1961.0157. ISSN 0080-4630. S2CID 121465295.
- 1 2 Hirsch, Peter; Whelan, Michael (1963). "Inelastic scattering of electrons by crystals. I. The theory of small-angle in elastic scattering". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 271 (1345): 268–287. Bibcode:1963RSPSA.271..268H. doi:10.1098/rspa.1963.0017. ISSN 0080-4630. S2CID 123122726.
- ↑ Ishizuka, Kazuo (2004). "FFT Multislice Method—The Silver Anniversary". Microscopy and Microanalysis. 10 (1): 34–40. Bibcode:2004MiMic..10...34I. doi:10.1017/S1431927604040292. ISSN 1431-9276. PMID 15306065. S2CID 8016041.
- ↑ Metherell, A. J. (1975). Electron Microscopy in Materials Science: Part II. Commission of the European Communities. pp. 397–552.
- ↑ Berry, M V (1971). "Diffraction in crystals at high energies". Journal of Physics C: Solid State Physics. 4 (6): 697–722. Bibcode:1971JPhC....4..697B. doi:10.1088/0022-3719/4/6/006. ISSN 0022-3719.
- 1 2 Gjønnes, J.; Moodie, A. F. (1965). "Extinction conditions in the dynamic theory of electron diffraction". Acta Crystallographica. 19 (1): 65–67. Bibcode:1965AcCry..19...65G. doi:10.1107/S0365110X65002773. ISSN 0365-110X.
- ↑ Lindhard, J. (1964). "Motion of swift charged particles, as influenced by strings of atoms in crystals". Physics Letters. 12 (2): 126–128. Bibcode:1964PhL....12..126L. doi:10.1016/0031-9163(64)91133-3.
- 1 2 McRae, E. G. (1966). "Multiple-Scattering Treatment of Low-Energy Electron-Diffraction Intensities". The Journal of Chemical Physics. 45 (9): 3258–3276. Bibcode:1966JChPh..45.3258M. doi:10.1063/1.1728101. ISSN 0021-9606.
- 1 2 Colella, R. (1972). "n -Beam dynamical diffraction of high-energy electrons at glancing incidence. General theory and computational methods". Acta Crystallographica Section A. 28 (1): 11–15. Bibcode:1972AcCrA..28...11C. doi:10.1107/S0567739472000026. ISSN 0567-7394.
- ↑ Kainuma, Y. (1955). "The Theory of Kikuchi patterns". Acta Crystallographica. 8 (5): 247–257. Bibcode:1955AcCry...8..247K. doi:10.1107/S0365110X55000832.
- 1 2 Faye, Jan (2019), "Copenhagen Interpretation of Quantum Mechanics", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Winter 2019 ed.), Metaphysics Research Lab, Stanford University, retrieved 2023-09-26
- 1 2 Gbur, Gregory J. (2019). Falling Felines and Fundamental Physics. Yale University Press. pp. 243–263. doi:10.2307/j.ctvqc6g7s.17. ISBN 978-0-300-23129-8. JSTOR j.ctvqc6g7s. S2CID 243353224.
- 1 2 3 4 Morniroli, Jean Paul (2004). Large-Angle Convergent-Beam Electron Diffraction Applications to Crystal Defects. Taylor & Francis. doi:10.1201/9781420034073. ISBN 9782901483052.
- 1 2 3 4 5 Hawkes, Peter; Kasper, Erwin (2018). Principles of Electron Optics Volume Two: Applied Geometric Optics (2nd ed.). Elsevier. pp. Chpts 36, 40, 41, 43, 49, 50. ISBN 978-0-12-813369-9.
- ↑ Spence, John C. H. (2017). High-resolution electron microscopy. Oxford University Press. ISBN 978-0-19-879583-4. OCLC 1001251352.
- ↑ J., Heinrich, K. F. (1981). Energy dispersive x-ray spectrometry. National Technical Information Service. OCLC 801808484.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ F., Egerton, R. (2011). Electron energy-loss spectroscopy in the electron microscope. Springer. ISBN 978-1-4419-9582-7. OCLC 706920411.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Cowley, J. M. (1992). "Twenty forms of electron holography". Ultramicroscopy. 41 (4): 335–348. doi:10.1016/0304-3991(92)90213-4. ISSN 0304-3991.
- 1 2 "Apertures, Electron Microscope Apertures". www.tedpella.com. Retrieved 2023-02-11.
- ↑ Honjo, Goro; Mihama, Kazuhiro (1954). "Fine Structure due to Refraction Effect in Electron Diffraction Pattern of Powder Sample Part II. Multiple Structures due to Double Refraction given by Randomly Oriented Smoke Particles of Magnesium and Cadmium Oxide". Journal of the Physical Society of Japan. 9 (2): 184–198. doi:10.1143/jpsj.9.184. ISSN 0031-9015.
- 1 2 Marks, L.D.; Sinkler, W. (2003). "Sufficient Conditions for Direct Methods with Swift Electrons". Microscopy and Microanalysis. 9 (5): 399–410. Bibcode:2003MiMic...9..399M. doi:10.1017/S1431927603030332. ISSN 1431-9276. PMID 19771696. S2CID 20112743.
- ↑ Kolb, U.; Gorelik, T.; Kübel, C.; Otten, M.T.; Hubert, D. (2007). "Towards automated diffraction tomography: Part I—Data acquisition". Ultramicroscopy. 107 (6–7): 507–513. doi:10.1016/j.ultramic.2006.10.007. ISSN 0304-3991. PMID 17234347.
- ↑ Mugnaioli, E.; Gorelik, T.; Kolb, U. (2009). ""Ab initio" structure solution from electron diffraction data obtained by a combination of automated diffraction tomography and precession technique". Ultramicroscopy. 109 (6): 758–765. doi:10.1016/j.ultramic.2009.01.011. ISSN 0304-3991. PMID 19269095.
- ↑ Howie, A.; Krivanek, O. L.; Rudee, M. L. (1973). "Interpretation of electron micrographs and diffraction patterns of amorphous materials". Philosophical Magazine. 27 (1): 235–255. Bibcode:1973PMag...27..235H. doi:10.1080/14786437308228927. ISSN 0031-8086.
- ↑ Howie, A. (1978). "High resolution electron microscopy of amorphous thin films". Journal of Non-Crystalline Solids. Proceedings of the Topical Conference on Atomic Scale Structure of Amorphous Solids. 31 (1): 41–55. Bibcode:1978JNCS...31...41H. doi:10.1016/0022-3093(78)90098-4. ISSN 0022-3093.
- ↑ Gibson, J. M.; Treacy, M. M. J. (1997). "Diminished Medium-Range Order Observed in Annealed Amorphous Germanium". Physical Review Letters. 78 (6): 1074–1077. Bibcode:1997PhRvL..78.1074G. doi:10.1103/PhysRevLett.78.1074. ISSN 0031-9007.
- ↑ Treacy, M M J; Gibson, J M; Fan, L; Paterson, D J; McNulty, I (2005). "Fluctuation microscopy: a probe of medium range order". Reports on Progress in Physics. 68 (12): 2899–2944. Bibcode:2005RPPh...68.2899T. doi:10.1088/0034-4885/68/12/R06. ISSN 0034-4885. S2CID 16316238.
- 1 2 Janner, A.; Janssen, T. (1977). "Symmetry of periodically distorted crystals". Physical Review B. 15 (2): 643–658. Bibcode:1977PhRvB..15..643J. doi:10.1103/physrevb.15.643. ISSN 0556-2805.
- 1 2 Bak, P (1982). "Commensurate phases, incommensurate phases and the devil's staircase". Reports on Progress in Physics. 45 (6): 587–629. doi:10.1088/0034-4885/45/6/001. ISSN 0034-4885.
- 1 2 Janssen, T.; Janner, A.; Looijenga-Vos, A.; de Wolff, P. M. (2006), Prince, E. (ed.), "Incommensurate and commensurate modulated structures", International Tables for Crystallography (1 ed.), Chester, England: International Union of Crystallography, vol. C, pp. 907–955, doi:10.1107/97809553602060000624, ISBN 978-1-4020-1900-5, retrieved 2023-03-24
- ↑ Randall, Clive A.; Fan, Zhongming; Reaney, Ian; Chen, Long-Qing; Trolier-McKinstry, Susan (2021). "Antiferroelectrics: History, fundamentals, crystal chemistry, crystal structures, size effects, and applications". Journal of the American Ceramic Society. 104 (8): 3775–3810. doi:10.1111/jace.17834. ISSN 0002-7820. S2CID 233534909.
- ↑ Heine, V; Samson, J H (1983). "Magnetic, chemical and structural ordering in transition metals". Journal of Physics F: Metal Physics. 13 (10): 2155–2168. Bibcode:1983JPhF...13.2155H. doi:10.1088/0305-4608/13/10/025. ISSN 0305-4608.
- ↑ "6.8: Ferro-, Ferri- and Antiferromagnetism". Chemistry LibreTexts. 2019-09-13. Retrieved 2023-09-26.
- ↑ Andersen, Tassie K.; Fong, Dillon D.; Marks, Laurence D. (2018). "Pauling's rules for oxide surfaces". Surface Science Reports. 73 (5): 213–232. Bibcode:2018SurSR..73..213A. doi:10.1016/j.surfrep.2018.08.001. S2CID 53137808.
- ↑ Oura, Kenjiro; Lifšic, Viktor G.; Saranin, A. A.; Zotov, A. V.; Katayama, Masao, eds. (2003). Surface science: an introduction; with 16 tables. Advanced texts in physics. Berlin Heidelberg: Springer. ISBN 978-3-540-00545-2.
- 1 2 Takayanagi, K.; Tanishiro, Y.; Takahashi, M.; Takahashi, S. (1985). "Structural analysis of Si(111)-7×7 by UHV-transmission electron diffraction and microscopy". Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films. 3 (3): 1502–1506. Bibcode:1985JVSTA...3.1502T. doi:10.1116/1.573160. ISSN 0734-2101.
- ↑ Ciston, J.; Subramanian, A.; Robinson, I. K.; Marks, L. D. (2009). "Diffraction refinement of localized antibonding at the Si(111) 7 × 7 surface". Physical Review B. 79 (19): 193302. arXiv:0901.3135. Bibcode:2009PhRvB..79s3302C. doi:10.1103/PhysRevB.79.193302. ISSN 1098-0121.
- ↑ Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J. W. (1984). "Metallic Phase with Long-Range Orientational Order and No Translational Symmetry". Physical Review Letters. 53 (20): 1951–1953. Bibcode:1984PhRvL..53.1951S. doi:10.1103/PhysRevLett.53.1951. ISSN 0031-9007.
- ↑ Widjaja, E.J.; Marks, L.D. (2003). "Microstructural evolution in Al–Cu–Fe quasicrystalline thin films". Thin Solid Films. 441 (1–2): 63–71. Bibcode:2003TSF...441...63W. doi:10.1016/S0040-6090(03)00903-9.
- ↑ Welberry, T. R. (2014). "One Hundred Years of Diffuse X-ray Scattering". Metallurgical and Materials Transactions A. 45 (1): 75–84. Bibcode:2014MMTA...45...75W. doi:10.1007/s11661-013-1889-2. ISSN 1073-5623. S2CID 137476417.
- ↑ Nield, Victoria M. (2001). Diffuse neutron scattering from crystalline materials. David A. Keen. Oxford: Clarendon Press. ISBN 0-19-851790-4. OCLC 45485010.
- ↑ Roth, N.; Beyer, J.; Fischer, K. F. F.; Xia, K.; Zhu, T.; Iversen, B. B. (2021). "Tuneable local order in thermoelectric crystals". IUCrJ. 8 (4): 695–702. doi:10.1107/S2052252521005479. ISSN 2052-2525. PMC 8256708. PMID 34258017.
- ↑ Chuvilin, A.; Kaiser, U. (2005). "On the peculiarities of CBED pattern formation revealed by multislice simulation". Ultramicroscopy. 104 (1): 73–82. doi:10.1016/j.ultramic.2005.03.003. PMID 15935917.
- ↑ Schnitzer, Noah; Sung, Suk Hyun; Hovden, Robert (2019). "Introduction to the Ronchigram and its Calculation with Ronchigram.com". Microscopy Today. 27 (3): 12–15. doi:10.1017/s1551929519000427. ISSN 1551-9295. S2CID 155224415.
- ↑ Own, C. S.: PhD thesis, System Design and Verification of the Precession Electron Diffraction Technique, Northwestern University, 2005, http://www.numis.northwestern.edu/Research/Current/precession.shtml
- ↑ Vincent, R.; Midgley, P.A. (1994). "Double conical beam-rocking system for measurement of integrated electron diffraction intensities". Ultramicroscopy. 53 (3): 271–282. doi:10.1016/0304-3991(94)90039-6.
- ↑ Gjønnes, J.; Hansen, V.; Berg, B. S.; Runde, P.; Cheng, Y. F.; Gjønnes, K.; Dorset, D. L.; Gilmore, C. J. (1998). "Structure Model for the Phase AlmFe Derived from Three-Dimensional Electron Diffraction Intensity Data Collected by a Precession Technique. Comparison with Convergent-Beam Diffraction". Acta Crystallographica Section A. 54 (3): 306–319. Bibcode:1998AcCrA..54..306G. doi:10.1107/S0108767397017030.
- ↑ Moeck, Peter; Rouvimov, Sergei (2010). "Precession electron diffraction and its advantages for structural fingerprinting in the transmission electron microscope". Zeitschrift für Kristallographie. 225 (2–3): 110–124. Bibcode:2010ZK....225..110M. doi:10.1524/zkri.2010.1162. ISSN 0044-2968. S2CID 52059939.
- 1 2 Ophus, Colin (2019). "Four-Dimensional Scanning Transmission Electron Microscopy (4D-STEM): From Scanning Nanodiffraction to Ptychography and Beyond". Microscopy and Microanalysis. 25 (3): 563–582. Bibcode:2019MiMic..25..563O. doi:10.1017/S1431927619000497. ISSN 1431-9276. PMID 31084643. S2CID 263414171.
- ↑ "4D STEM | Gatan, Inc". www.gatan.com. Retrieved 2022-03-13.
- ↑ Hage, Fredrik S.; Nicholls, Rebecca J.; Yates, Jonathan R.; McCulloch, Dougal G.; Lovejoy, Tracy C.; Dellby, Niklas; Krivanek, Ondrej L.; Refson, Keith; Ramasse, Quentin M. (2018). "Nanoscale momentum-resolved vibrational spectroscopy". Science Advances. 4 (6): eaar7495. Bibcode:2018SciA....4.7495H. doi:10.1126/sciadv.aar7495. ISSN 2375-2548. PMC 6018998. PMID 29951584.
- ↑ Gilmore, C.J.; Marks, L.D.; Grozea, D.; Collazo, C.; Landree, E.; Twesten, R.D. (1997). "Direct solutions of the Si(111) 7 × 7 structure". Surface Science. 381 (2–3): 77–91. Bibcode:1997SurSc.381...77G. doi:10.1016/S0039-6028(97)00062-9.
- ↑ Robinson, I. K. (1983). "Direct Determination of the Au(110) Reconstructed Surface by X-Ray Diffraction". Physical Review Letters. 50 (15): 1145–1148. Bibcode:1983PhRvL..50.1145R. doi:10.1103/PhysRevLett.50.1145. ISSN 0031-9007.
- ↑ Enterkin, James A.; Subramanian, Arun K.; Russell, Bruce C.; Castell, Martin R.; Poeppelmeier, Kenneth R.; Marks, Laurence D. (2010). "A homologous series of structures on the surface of SrTiO3(110)". Nature Materials. 9 (3): 245–248. Bibcode:2010NatMa...9..245E. doi:10.1038/nmat2636. ISSN 1476-4660. PMID 20154691.
- ↑ Kienzle, Danielle M.; Marks, Laurence D. (2012). "Surface transmission electron diffraction for SrTiO3 surfaces". CrystEngComm. 14 (23): 7833. doi:10.1039/c2ce25204j. ISSN 1466-8033.
- 1 2 Braun, Wolfgang (1999). Applied RHEED : reflection high-energy electron diffraction during crystal growth. Berlin: Springer. pp. Chpts 2–4, 7. ISBN 3-540-65199-3. OCLC 40857022.
- 1 2 3 Oberhammer, H. (1989). "I. Hargittai, M. Hargittai (Eds.): The Electron Diffraction Technique, Part A von: Stereochemical Applications of Gas-Phase Electron Diffraction, VCH Verlagsgesellschaft, Weinheim, Basel. Cambridge, New York 1988. 206 Seiten, Preis: DM 210,-". Berichte der Bunsengesellschaft für physikalische Chemie. 93 (10): 1151–1152. doi:10.1002/bbpc.19890931027. ISSN 0005-9021.
- 1 2 3 Schåfer, Lothar (1976). "Electron Diffraction as a Tool of Structural Chemistry". Applied Spectroscopy. 30 (2): 123–149. Bibcode:1976ApSpe..30..123S. doi:10.1366/000370276774456381. ISSN 0003-7028. S2CID 208256341.
- 1 2 Seip, H.M.; Strand, T.G.; Stølevik, R. (1969). "Least-squares refinements and error analysis based on correlated electron diffraction intensities of gaseous molecules". Chemical Physics Letters. 3 (8): 617–623. Bibcode:1969CPL.....3..617S. doi:10.1016/0009-2614(69)85125-0.
- 1 2 Andersen, B.; Seip, H. M.; Strand, T. G.; Stølevik, R.; Borch, Gunner; Craig, J. Cymerman (1969). "Procedure and Computer Programs for the Structure Determination of Gaseous Molecules from Electron Diffraction Data". Acta Chemica Scandinavica. 23: 3224–3234. doi:10.3891/acta.chem.scand.23-3224. ISSN 0904-213X.
- ↑ Lengyel, SáNdor; KáLmáN, Erika (1974). "Electron diffraction on liquid water". Nature. 248 (5447): 405–406. Bibcode:1974Natur.248..405L. doi:10.1038/248405a0. ISSN 0028-0836. S2CID 4201332.
- ↑ Kálmán, E.; Pálinkás, G.; Kovács, P. (1977). "Liquid water: I. Electron scattering". Molecular Physics. 34 (2): 505–524. doi:10.1080/00268977700101871. ISSN 0026-8976.
- ↑ de Kock, M. B.; Azim, S.; Kassier, G. H.; Miller, R. J. D. (2020-11-21). "Determining the radial distribution function of water using electron scattering: A key to solution phase chemistry". The Journal of Chemical Physics. 153 (19). Bibcode:2020JChPh.153s4504D. doi:10.1063/5.0024127. hdl:21.11116/0000-0007-6FBC-A. ISSN 0021-9606. PMID 33218233. S2CID 227100401.
- ↑ Dingley, D. J.; Randle, V. (1992). "Microtexture determination by electron back-scatter diffraction". Journal of Materials Science. 27 (17): 4545–4566. Bibcode:1992JMatS..27.4545D. doi:10.1007/BF01165988. ISSN 0022-2461. S2CID 137281137.
- ↑ Adams, Brent L.; Wright, Stuart I.; Kunze, Karsten (1993). "Orientation imaging: The emergence of a new microscopy". Metallurgical Transactions A. 24 (4): 819–831. Bibcode:1993MTA....24..819A. doi:10.1007/BF02656503. ISSN 0360-2133. S2CID 137379846.
- ↑ Dingley, D. (2004). "Progressive steps in the development of electron backscatter diffraction and orientation imaging microscopy: EBSD AND OIM". Journal of Microscopy. 213 (3): 214–224. doi:10.1111/j.0022-2720.2004.01321.x. PMID 15009688. S2CID 41385346.
- 1 2 Schwartz, Adam J; Kumar, Mukul; Adams, Brent L; Field, David P (2009). Electron backscatter diffraction in materials science. Springer New York. ISBN 978-1-4899-9334-2. OCLC 902763902.
Further reading
- John M., Cowley (1995). Diffraction physics. Elsevier. ISBN 0-444-82218-6. OCLC 247191522.. Contains extensive coverage of kinematical and other diffraction.
- Reimer, Ludwig (2013). Transmission Electron Microscopy : Physics of Image Formation and Microanalysis. Springer Berlin / Heidelberg. ISBN 978-3-662-13553-2. OCLC 1066178493. Large coverage of many different areas of electron microscopy with large numbers of references.
- Hirsch, P. B.; Howie, A.; Nicholson, R. B.; Pashley, D. W.; Whelan, M. J. (1965). Electron microscopy of thin crystals. London: Butterworths. ISBN 0-408-18550-3. OCLC 2365578., often called the bible of electron microscopy.
- Spence, J. C. H.; Zuo, J. M. (1992). Electron Microdiffraction. Boston, MA: Springer US. doi:10.1007/978-1-4899-2353-0. ISBN 978-1-4899-2355-4. S2CID 45473741., a large coverage of topic related to dynamical diffraction and CBED
- Peng, L.-M.; Dudarev, S. L.; Whelan, M. J. (2011). High energy electron diffraction and microscopy. Oxford: Oxford University Press. ISBN 978-0-19-960224-7. OCLC 656767858.. Very extensive coverage of modern dynamical diffraction.
- Carter, C. Barry; Williams, David B.; Thomas, John M., eds. (2016). Transmission electron microscopy: diffraction, imaging, and spectrometry. Cham, Switzerland: Springer. ISBN 978-3-319-26649-7., a recent textbook with many images, stronger on experimental aspects.
- Edington, Jeffrey William (1977). Practical electron microscopy in materials science. Techbooks. OCLC 27997701., an older source for experimental details, albeit hard to find.




.svg.png.webp)
